用 Java 深入研究树，你了解多少？-51CTO.COM

树数据结构在我们编码和面试中都是很重要的知识。使用数据结构来组织数据，数据结构越高效，程序就会越好。

今天，我们将深入探讨数据结构之一：树。

今天，我们将介绍：

什么是树？
树的种类
树的遍历和搜索

什么是树？

数据结构用于存储和组织数据。我们可以使用算法来操纵和使用我们的数据结构。通过使用不同的数据结构可以更有效地组织不同类型的数据。

树是非线性数据结构。它们通常用于表示分层数据。举一个现实的例子，分层的公司结构使用树来组织。

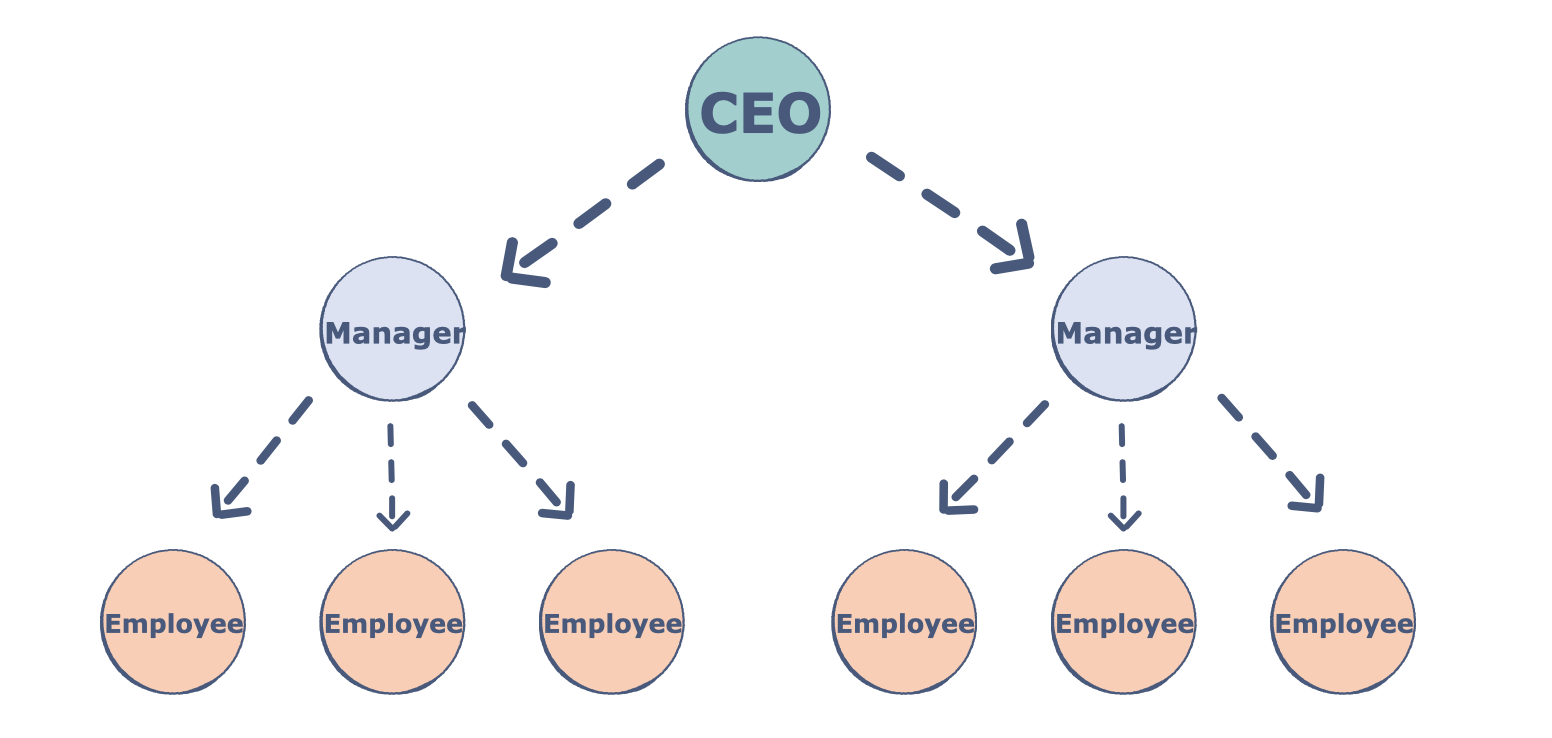
树的组成部分

树是节点（顶点）的集合，它们通过边（指针）链接起来，代表节点之间的层次连接。节点包含任意类型的数据，但所有节点必须具有相同的数据类型。树与图类似，但树中不能存在环。树有哪些不同的组成部分？

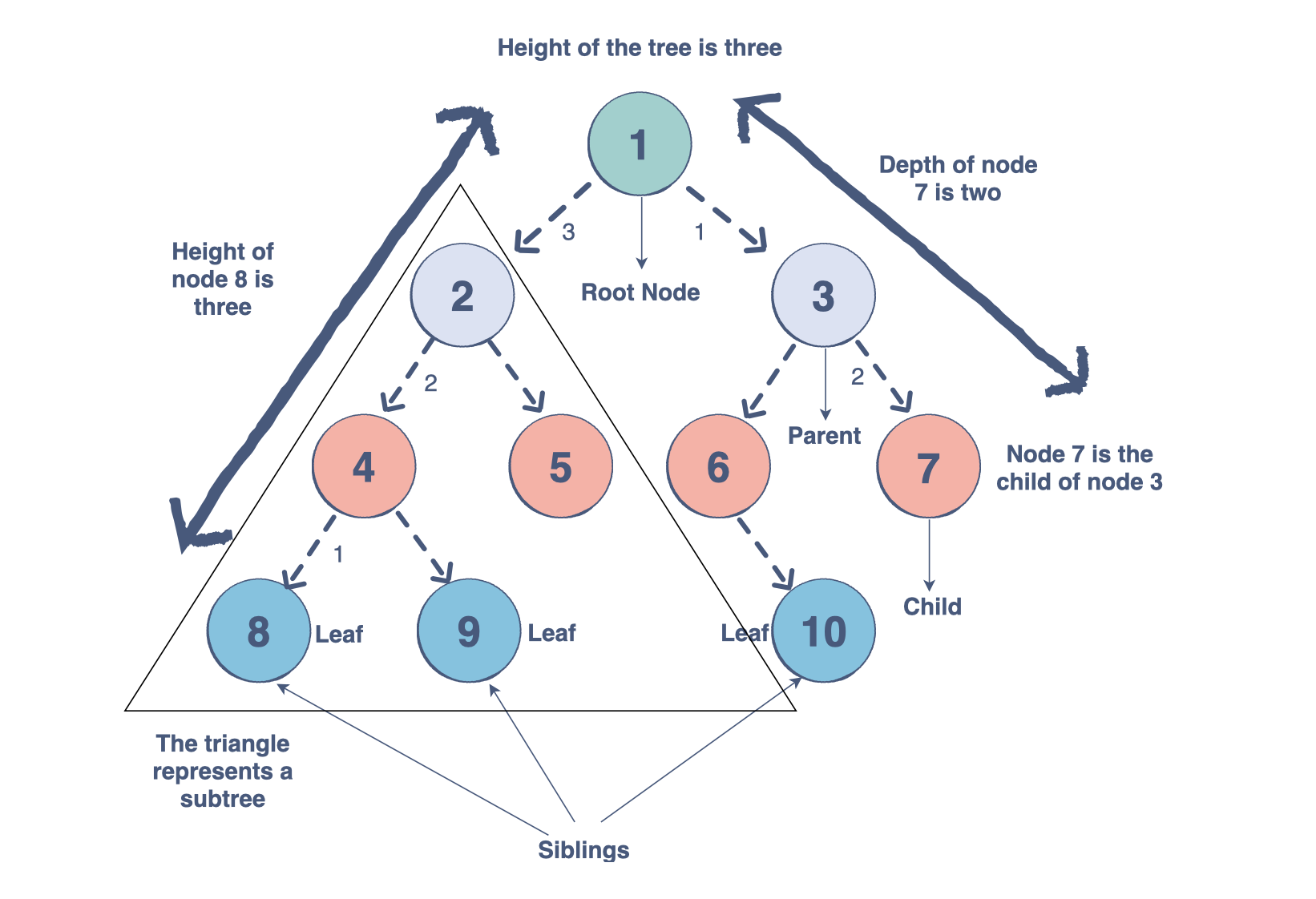
根：树的根是没有传入链接的节点（即没有父节点）。将此视为树的起点。

子节点：树的子节点是一个节点，具有来自其上方节点（即父节点）的一个传入链接。如果两个子节点共享同一个父节点，则它们称为兄弟节点。

父节点：父节点具有将其连接到一个或多个子节点的传出链接。

叶子：叶子有一个父节点，但没有到子节点的传出链接。将此视为树的端点。

子树：子树是包含在较大树中的较小树。该树的根可以是较大树中的任何节点。

深度：节点的深度是该节点与根之间的边数。将此视为节点和树的起点之间有多少步。

高度：节点的高度是从该节点到叶节点的最长路径中的边数。将此视为节点和树端点之间有多少步。树的高度是其根节点的高度。

度：节点的度是指子树的数量。

我们为什么要使用树？

树可以应用于很多事情。层次结构赋予树用于存储、操作和访问数据的独特属性。树构成了计算机最基本的组织结构。我们可以将树用于以下用途：

存储为层次结构。存储层次结构中自然出现的信息。计算机上的文件系统和 PDF 使用树结构。
搜索。存储我们想要快速搜索的信息。树比链表更容易搜索。某些类型的树（如 AVL 树和红黑树）是为快速搜索而设计的。
继承。树可用于继承、XML 解析器、机器学习和 DNS 等。
索引。高级类型的树（例如 B 树和 B+ 树）可用于为数据库建立索引。
网络。树非常适合社交网络和电脑国际象棋游戏等。
最短路径。生成树可用于查找路由器中的最短路径以进行网络连接。
等等

如何编码一棵树

例如，要在Java中构建树，我们从根节点开始。

Node<String> root = new Node<>("root");

一旦我们有了根，我们就可以使用添加第一个子节点addChild，这会添加一个子节点并将其分配给父节点。我们将此过程称为插入（添加节点）和删除（删除节点）。

Node<String> node1 = root.addChild(new Node<String>("node 1"));

我们继续使用相同的过程添加节点，直到我们拥有复杂的层次结构。

树的种类

我们可以使用多种类型的树在层次结构中以不同的方式组织数据。我们使用的树取决于我们要解决的问题。让我们看一下可以在 Java 中使用的树。我们将涵盖：

N叉树
平衡树
二叉树
二叉搜索树
AVL树
红黑树
2-3 棵树
2-3-4 树

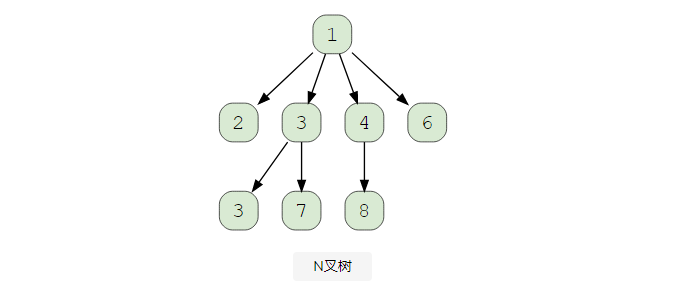
N叉树

在N叉树中，一个节点可以有0-N个子节点。例如，如果我们有一个二叉树（也称为二叉树），它最多有 0-2 个子节点。

注：节点的平衡因子是左右子树的高度差。

平衡树

平衡树是几乎所有叶子节点都在同一级别的树，最常应用于子树，即所有子树都必须是平衡的。换句话说，我们必须使树高平衡，左右子树的高度差不超过1。这是平衡树的直观表示。

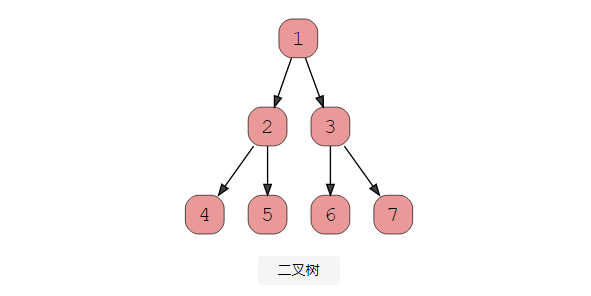
根据其结构，二叉树主要分为三种类型。

1、完全二叉树

当每一层（不包括最后一层）都被填满并且最后一层的所有节点都尽可能靠左时，就存在完全二叉树。这是完整二叉树的直观表示。

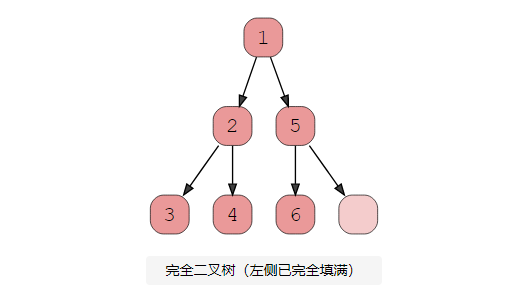
2、满二叉树

当每个节点（不包括叶子）都有两个子节点时，就存在满二叉树（有时称为真二叉树）。每一层都必须填满，并且节点尽可能远离。查看此图以了解完整二叉树的外观。

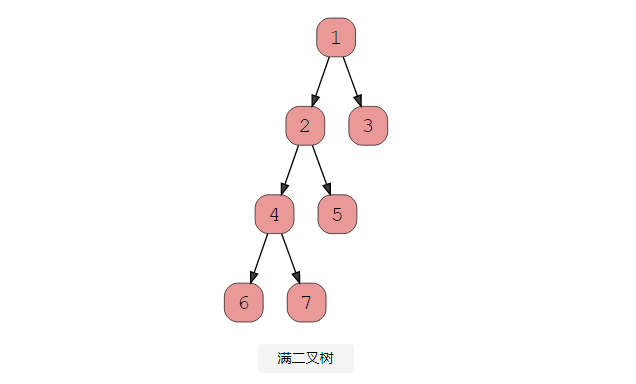
3、完美二叉树

完美的二叉树应该是满的和完整的。所有内部节点都应该有两个子节点，并且所有叶子节点必须具有相同的深度。查看此图以了解完美二叉树的外观。

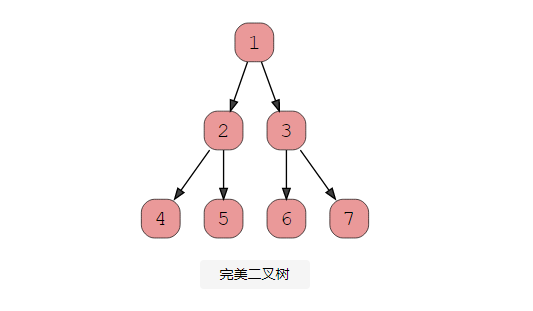
注意：还可以拥有倾斜二叉树，其中所有节点都向左或向右移动，但最佳实践是在 Java 中避免这种类型的树，因为搜索节点要复杂得多。

二叉搜索树

二叉搜索树是一棵二叉树，其中每个节点都有一个键和一个关联值。这允许快速查找和编辑（添加或删除），因此得名“搜索”。二叉搜索树根据其node值有严格的条件。需要注意的是，每个二叉搜索树都是二叉树，但并非每个二叉树都是二叉搜索树。

是什么让他们与众不同？在二叉搜索树中，子树的左子树必须包含键少于该节点键的节点，而右子树将包含键大于该节点键的节点。查看此视觉效果以了解这种情况。

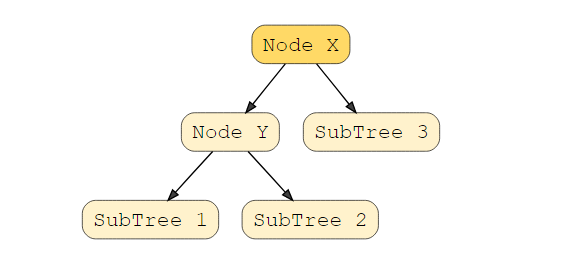
在此示例中，节点 Y 是具有两个子节点的父节点。子树 1 中的所有节点的值必须小于节点 Y，子树 2 中的所有节点的值必须大于节点 Y。

AVL树

AVL树是一种特殊类型的二叉搜索树，它通过检查每个节点的平衡因子来实现自平衡。平衡因子应该是+1、0或-1。左右子树的最大高度差只能为1。

如果这种差异变得大于一个，我们必须使用旋转技术重新平衡我们的树以使其有效。这些对于搜索是最重要操作的应用程序来说是最常见的。查看此视觉效果可以看到有效的 AVL 树。

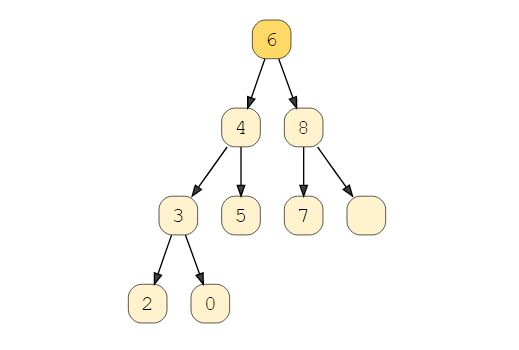
红黑树

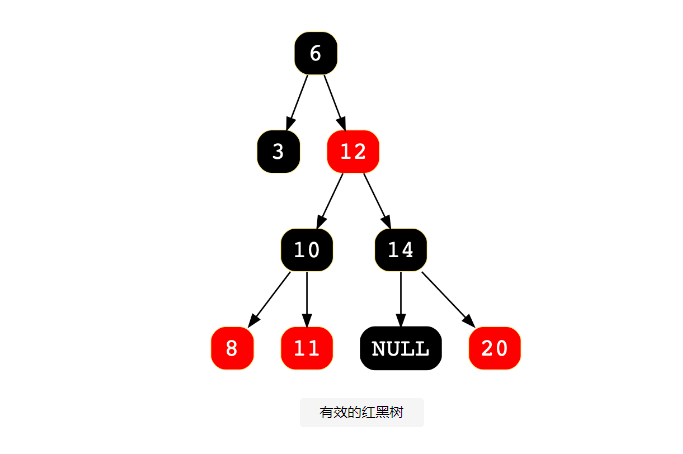
红黑树是另一种自平衡二叉搜索树，但它具有 AVL 树的一些附加属性。节点的颜色为红色或黑色，以帮助在插入或删除后重新平衡树。它们可以节省平衡时间。那么，我们如何为节点着色呢？

根部始终是黑色的。
两个红色节点不能相邻（即红色父节点不能有红色子节点）。
从根到叶的路径应包含相同数量的黑色节点。
空节点是黑色的。

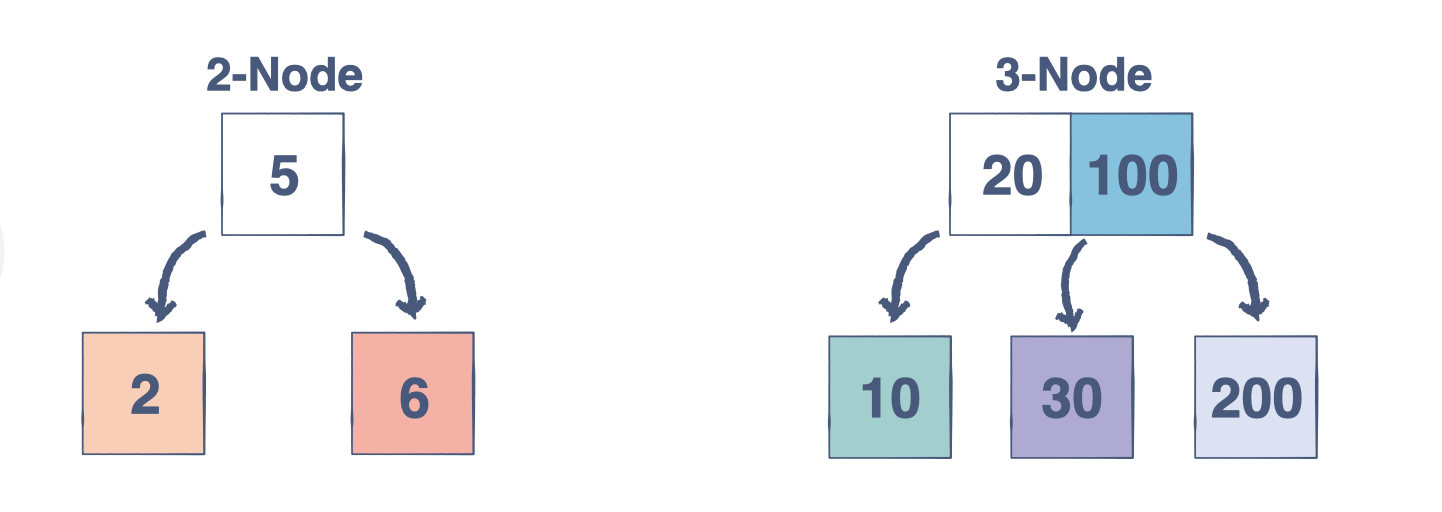
2-3 棵树

2-3 树与我们目前学到的有很大不同。与二叉搜索树不同，2-3 树是一种自平衡、有序、多路搜索树。它始终是完美平衡的，因此每个叶节点与根的距离相等。除叶节点外，每个节点都可以是 2 节点（具有单个数据元素和两个子节点的节点）或 3 节点（具有两个数据元素和三个子节点的节点）。无论发生多少次插入或删除，2-3 树都会保持平衡。

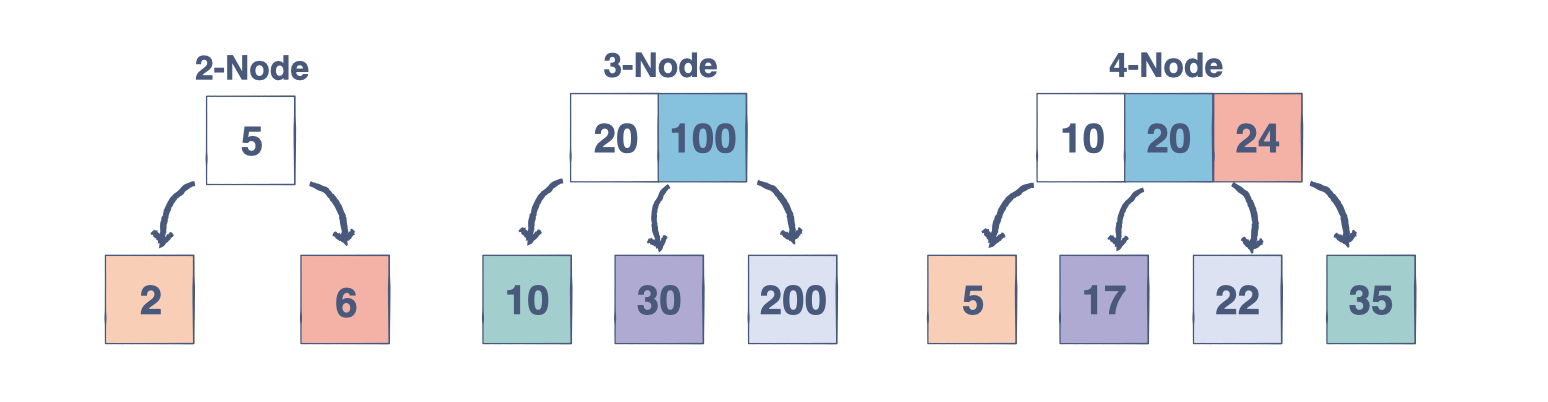
2-3-4 树

2-3-4 树是一种比 2-3 树可以容纳更多键的搜索树。它涵盖了与 2-3 树相同的基础知识，但添加了以下属性：

2-节点有两个子节点和一个数据元素
3-Node 有三个子节点和两个数据元素
4-节点有四个子节点和三个数据元素
每个内部节点最多有 4 个子节点
对于内部节点的三个键，LeftChild节点的所有键都小于左键
LeftMidChild 上的所有键都小于中间键
RightMidChild 处的所有键都小于右侧键
RightChild 处的所有键都大于右侧键

树遍历和搜索简介

要使用树，我们可以通过访问/检查树的每个节点来遍历它们。如果一棵树被“遍历”，这意味着每个节点都被访问过。遍历一棵树有四种方法。这四个过程属于两类之一：广度优先遍历或深度优先遍历。

中序：将其视为在树上向上移动，然后向下移动。遍历左子树及其子树，直到到达根。然后，向下遍历右孩子及其子树。这是深度优先遍历。
前序：从根开始，遍历左子树，然后移动到右子树。这是深度优先遍历。
后序：从左子树开始，移至右子树。然后，向上移动访问根节点。这是深度优先遍历。
层序：将其视为一种之字形图案。这将按节点的级别而不是子树遍历节点。首先，我们访问根并从左到右访问该根的所有子节点。然后我们向下移动到下一个级别，直到到达没有子节点的节点。这是左节点。这是广度优先的遍历。

那么，广度优先遍历和深度优先遍历有什么区别呢？让我们看一下深度优先搜索 (DFS) 和广度优先搜索 (BFS) 算法，以便更好地理解这一点。

注意：算法是用于执行某些任务的指令序列。我们使用具有数据结构的算法来操作我们的数据，在本例中是遍历我们的数据。

深度优先搜索

概述：我们沿着从起始节点到结束节点的路径，然后开始另一条路径，直到访问完所有节点。这通常使用堆栈来实现，并且它比 BFS 需要更少的内存。它最适合拓扑排序，例如图回溯或循环检测。

算法步骤DFS如下：

选择一个节点。将所有相邻节点压入堆栈。
从该堆栈中弹出一个节点并将相邻节点推入另一个堆栈。
重复此步骤，直到堆栈为空或达到目标为止。当访问节点时，必须在继续之前将其标记为已访问，否则将陷入无限循环。

广度优先搜索

概述：我们逐级访问一级的所有节点，然后再进入下一级。BFS算法通常使用队列来实现，并且它比DFS算法需要更多的内存。最适合寻找两个节点之间的最短路径。

算法步骤BFS如下：

选择一个节点。将所有相邻节点放入队列中。将节点出队，并将其标记为已访问。将所有相邻节点放入另一个队列中。
重复此操作，直到队列中没有已实现的目标。
当访问节点时，必须在继续之前将其标记为已访问，否则将陷入无限循环。

在二叉搜索树中搜索

了解如何在树中执行搜索非常重要。搜索意味着我们在数据结构中定位特定元素或节点。由于二叉搜索树中的数据是有序的，因此搜索非常容易。让我们看看它是如何完成的。

从根开始。
如果该值小于当前节点的值，则遍历左子树。如果大于，则遍历右子树。
继续此过程，直到到达具有该值的节点或到达叶节点，这意味着该值不存在。

在3.中步骤，如下：

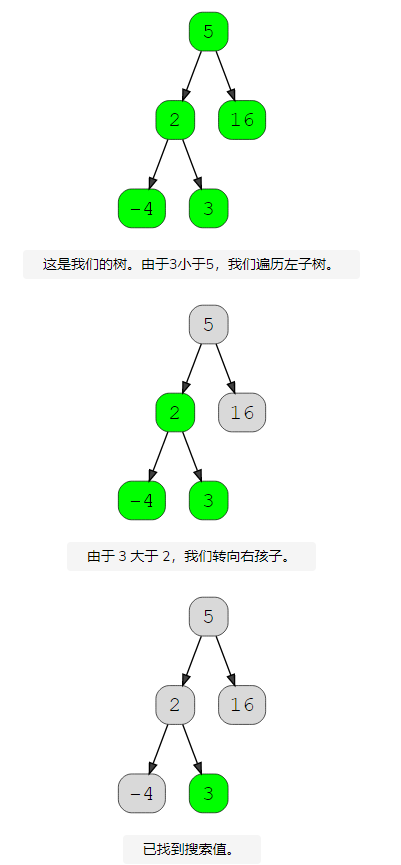
现在让我们看看 Java 代码中的内容！

public class BinarySearchTree {
      …
      
      public boolean search(int value) {
            if (root == null)
                  return false;
            else
                  return root.search(value);
      }
}
public class BSTNode {
      …

      public boolean search(int value) {
            if (value == this.value)
                  return true;
            else if (value < this.value) {
                  if (left == null)
                        return false;
                  else
                        return left.search(value);
            } else if (value > this.value) {
                  if (right == null)
                        return false;
                  else
                        return right.search(value);
            }
            return false;
      }
}

总结

本篇让我们更深入了解树的数据结构以及用的运用。