数据结构分类
数据结构是计算机中组织和存储数据的方式。
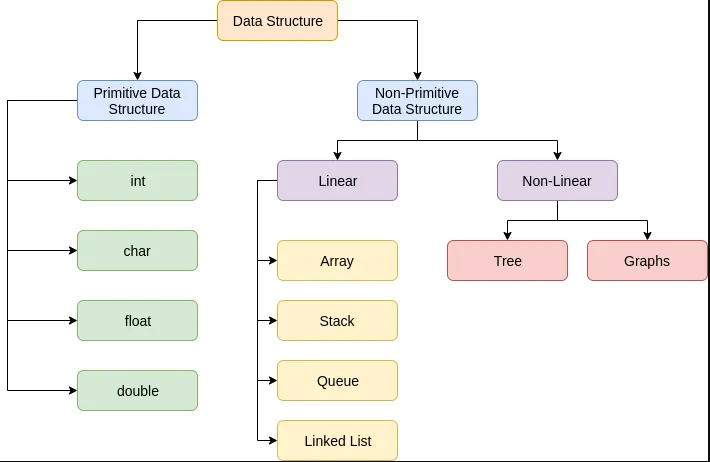
数据结构分类-原始与非原始
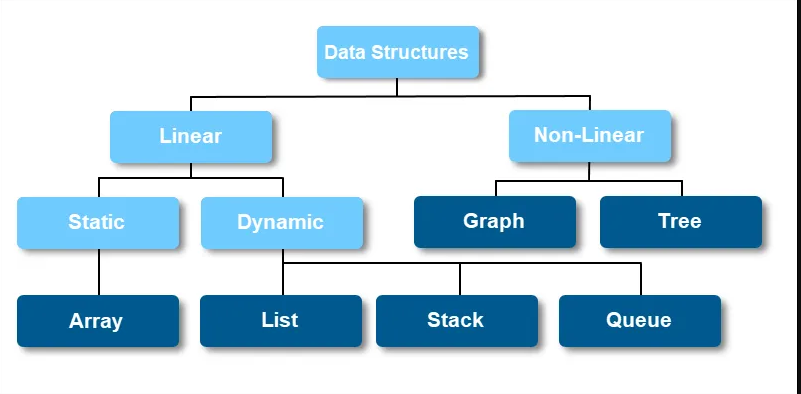
数据结构分类-线性与非线性
原始数据结构
基本数据结构不能进一步划分。
- 具有算术运算的 8 位整数(字节)— 最小值为 -128,最大值为 127(含)。
- 具有算术运算的 16 位整数(短整型)— 最小值为 -32,768,最大值为 32,767(含)。
- 具有算术运算的 32 位整数 (Int) — 最小值为 -231,最大值为 230。
- 具有算术运算的 64 位整数(长整型)— 最小值为 -263,最大值为 262。
- 16 位 Unicode 字符/字母数字字符/符号 (char) — 最小值'\u0000'(或 0)和最大值'\uffff'(或 65,535(含))。
- 带算术运算的单精度 32 位 IEEE 754 实数(浮点型)。
- 带算术运算的双精度 64 位 IEEE 754 实数 (Double)。
- 布尔值(具有逻辑运算(布尔)的值 { true, false} 的集合 - 只有两个可能的值:true和false。
非原始数据结构
- 数据结构可用于其他复杂的存储。
线性
- 元素组成一个序列
数组(Array)
- 它是相同类型元素的集合。
- 元素按顺序连续存储。
- 利用索引可以计算出元素对应的地址。
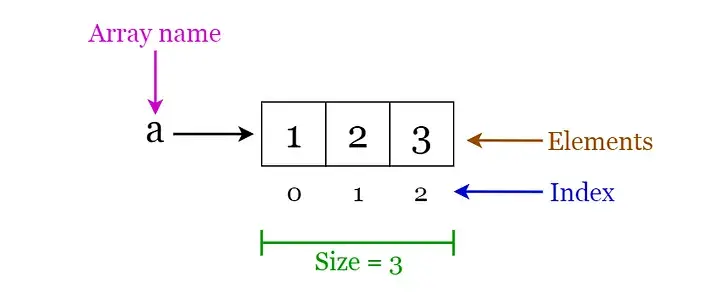
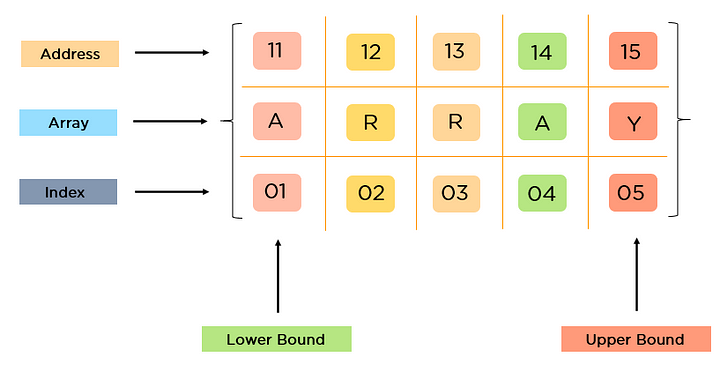
Array
- 一维数组——元素是线性存储的,可以通过指定数组中存储的每个元素的索引值来单独访问
- int a[n],string a[n]
- 多维数组——具有多个维度的数组
- int a[m][n],string a[m][n]
特征
- 所请求的内存空间的大小是固定的并且不能改变。使用前必须提前申请内存空间。
- 数组实现数学向量和矩阵,以及其他类型的矩形表。
优点
- 按索引读取效率高(支持随机访问应用)
- 搜索:时间复杂度为O(1)
缺点
- 写入效率低(删除和插入效率比较低,因为取决于插入和删除的位置,需要做大量的数据移动,除非插入和删除的位置是最后一位
- 插入/删除:时间复杂度为O(n)
链表(Linked List)
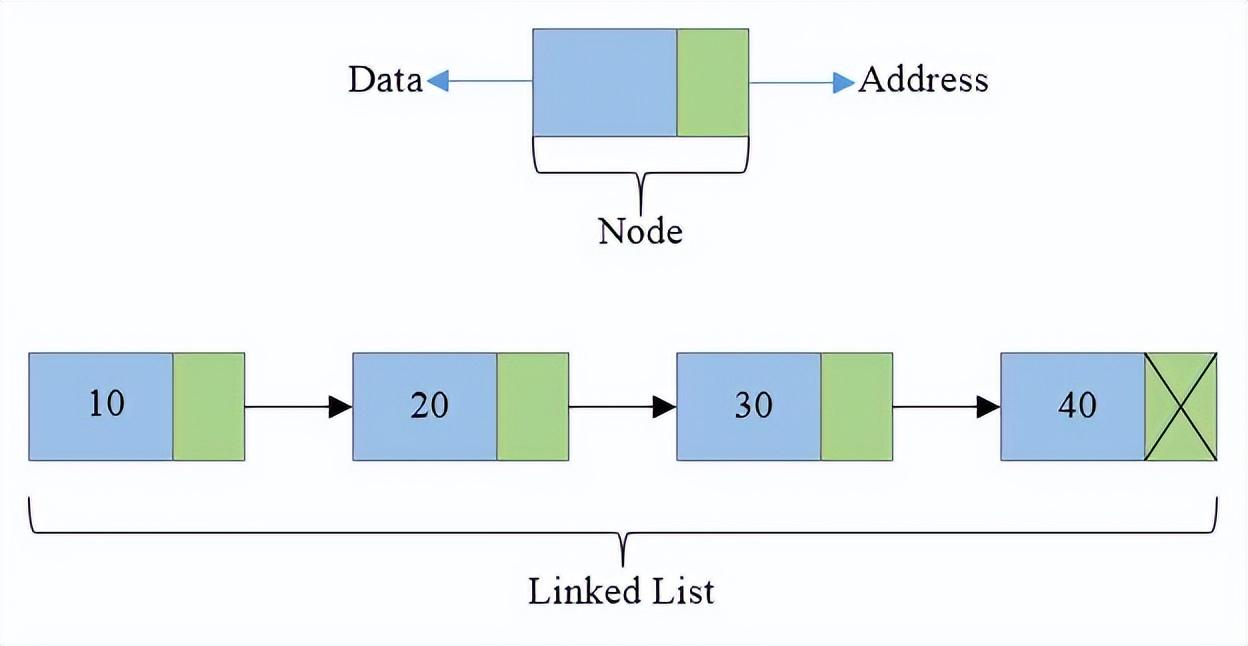
- 它是一种链式存储结构,其中前一个元素的引用指向下一个元素,链表通过指针将元素与元素连接起来。所以,它不是按顺序实现的,而是用指针实现的。
- 链表由一系列节点组成(每个节点由2部分组成:一个是存储数据元素的数据字段,另一个是存储下一个节点地址的指针字段
- 单链表、双向链表和循环链表
- 链表中元素的插入和删除比较简单,因为不需要移动元素和实现长度扩展,但查询一个元素比较困难
- 搜索:时间复杂度为O(n)
- 插入/删除:时间复杂度为O(1)
优点
- 可以任意添加或减少元素。
缺点
- 包含大量的指针字段,占用内存空间大
堆栈(Stack)
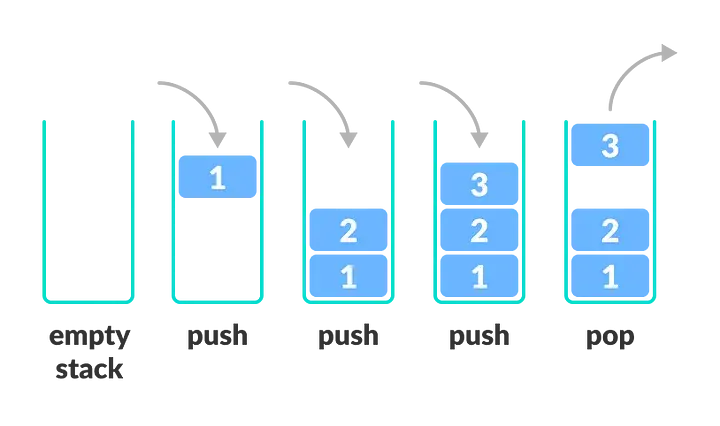
Stack
- 它是一种特殊的线性表,只能在一端插入和删除。
- 它按照后进先出(LIFO)的原则存储数据。
- 最先输入的数据被压入栈底,最后一个数据元素在栈顶。
- 最后一个数据元素首先被读出或从堆栈顶部弹出。
- 插入=Push
- 删除=Pop
- 栈中元素个数为零=空栈
- 插入/删除:时间复杂度为O(1)
队列(Queue)
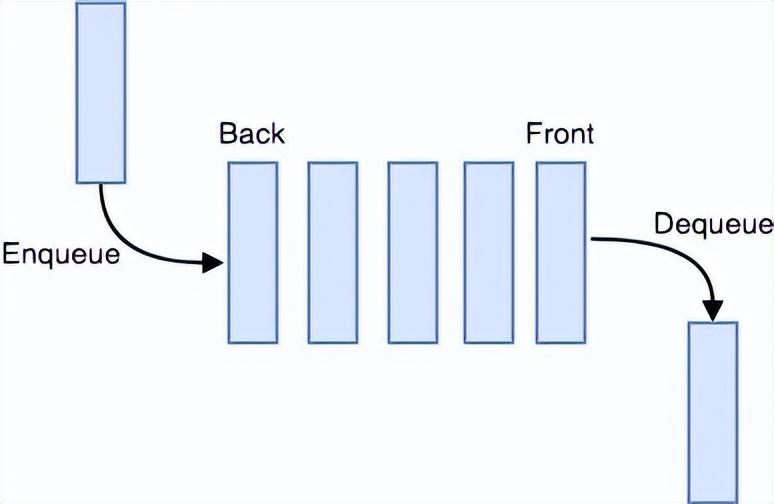
Queue
- 它是一个线性列表,允许在一端插入并在另一端删除。
- 它的运行原理是先进先出(FIFO)
基本操作
Enqueue:向队列中插入一个元素。
Dequeue:移除一个元素并返回队列的第一个元素。
- 插入/删除:时间复杂度为O(1)
- 循环队列、优先队列
非线性
- 它是一种数据结构形式,其中数据元素不保持线性或顺序排列
树(Tree)
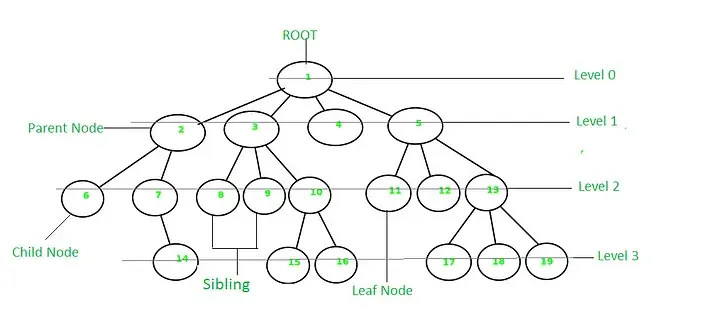
Tree
- 它是一种非线性存储,由n(n≥1)个有限节点组成具有层次关系的集合
- 它显示具有“一对多”关系的数据元素的集合
- 每个节点有零个或多个子节点
- 没有父节点的节点=根节点
- 每个非根节点有且只有一个父节点
- 每个子节点可以分为多个不相交的子树
- 节点深度=从根节点到x节点的路径长度。根节点深度为0,第二层节点深度为1,以此类推
- 节点高度=叶子节点到x节点的路径长度
- 节点的度=节点的子树数量
- 叶节点= 度数为零的节点
二叉树
- 每个节点最多有2个子树,节点的最大度数为2
- 左子树和右子树是有序的,顺序不能颠倒
- 即使一个节点只有1个子树,也需要区分左右子树
- AVL树、红黑树、拉伸树、替罪羊树、B树、B+树、B*树、字典树(Trie树)
哈希表(Hash table)
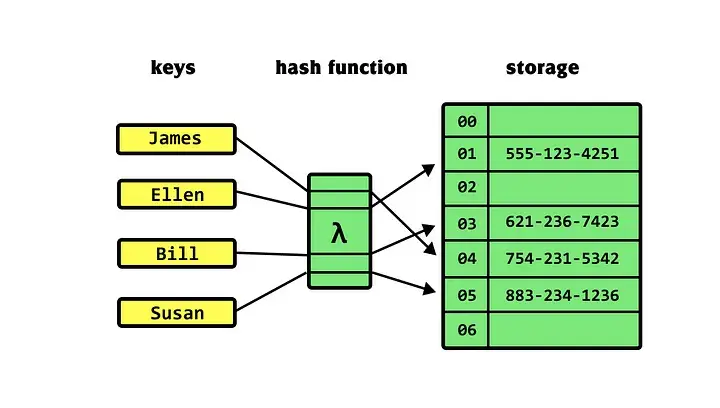
Hash table
- 它是一种根据映射函数直接访问的特殊数据结构,以key:value的形式存储数据。
- f(key) = 存储位置。
- 哈希表就是通过哈希函数将唯一标识转换成对应的位置。
- 查找、插入:时间复杂度为O(1)。
- 但是,如果哈希值都映射到同一个地址,则查找的时间复杂度为O(n)。
- 链接寻址——哈希函数将键值映射到哈希表中的每个位置。
- 开放寻址— 如果存在位置映射冲突,其中键 1 和键 2 共享相同位置,则将键 2 放入空空间并启动寻找空闲位置的过程。
- 检测方法 = 线性探测、二次探测、双重散列。
堆(Heap)
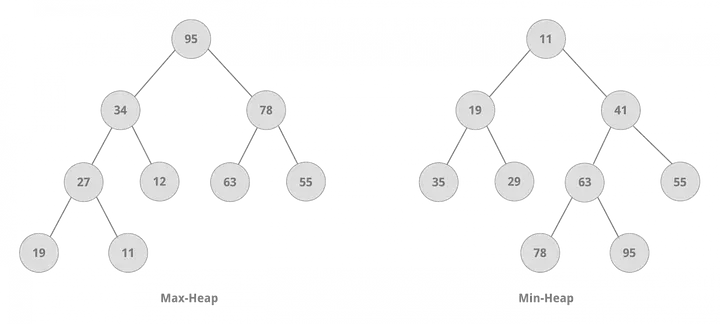
Heap
- 它是一个完全二叉树。
- 它是一个图树结构,用于实现“优先级队列”。
- 堆中节点的值始终不大于或小于其父节点的值。
- Min Heap = 根节点最小的堆,满足 ki ≤ K2i+1 且 ki ≤ k2i+2。
- Max Heap = 根节点最大的堆,满足 ki ≥ k2i+1 且 ki ≥ k2i+2。
图表(Graph)
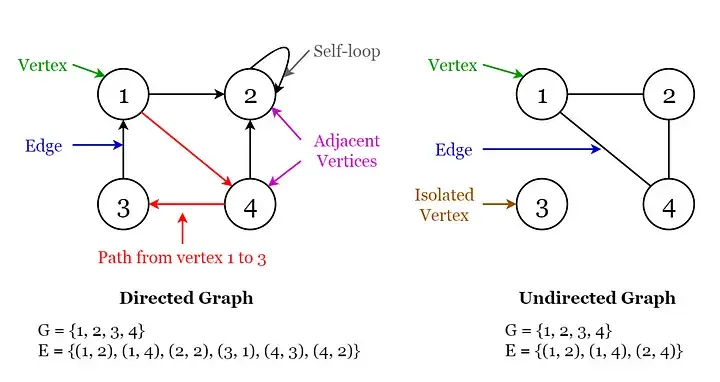
图形术语的可视化
- 它是一种相对复杂的数据结构,具有相对复杂且高效的数据存储算法。
- 它展示了对象与对象之间复杂的“多对多”关系。
- 它由有限的顶点集 V 和边集 E 组成。
可分为无向图和有向图:
- (v,w)表示无向边,即v和w是互连的。
- <v, w> 表示从 v 开始到 w 结束的有向边。
图可以分为加权图和未加权图:
- 加权图:每条边都有一定的权重,通常是一个数字。
- 无权图:每条边没有权重,也可以理解为权重为1。
图可以分为连通图和非连通图:
- 连通图:所有点都通过路径连接。
- 断开图:有两个点没有通过路径连接。
图中的顶点有度的概念:
- 度数——与其相连的所有点的总和。
- 入度 — 存在于有向图中,访问该点的所有边的总和。
- 出度——存在于有向图中,与该点相连的边数之和。
图表的表示
- 邻接矩阵— 具有 n 个顶点的图需要具有大小为 nxn 的矩阵。
- 邻接表- 具有链表数组的图。
- 算法:图的搜索算法、广度优先搜索(BFS)、深度优先搜索(DFS)等。
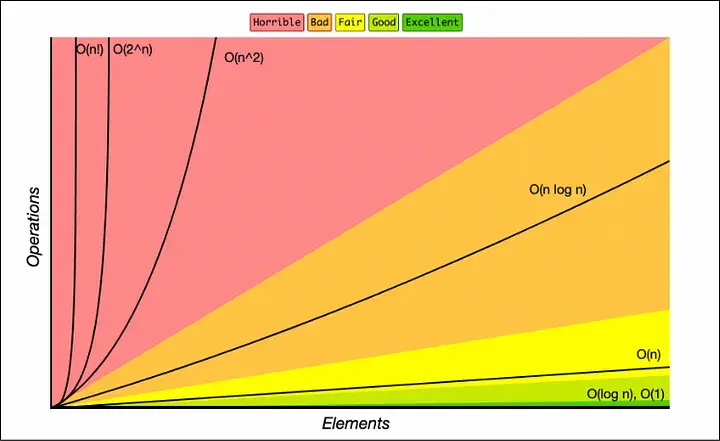
大O复杂性