译者 | 朱先忠
审校 | 重楼
简介
层次聚类算法（Agglomerative Clustering）是数据科学中最好的聚类工具之一，但传统的实现无法扩展到大型数据集领域。
在这篇文章中，我将带你了解层次聚类算法的一些背景，基于谷歌2021年的研究介绍交互式层次聚类（RAC）算法、RAC++算法和Scikit Learn的层次聚类算法的运行时效果比较，最后将简要探讨一下RAC算法背后的理论支持。
层次聚类算法的背景
在数据科学领域，对未标记的数据进行聚类通常是非常有用的。从搜索引擎结果的分组到基因型分类，再到银行异常检测，聚类已经成为数据科学家们的工具包中必不可少的一部分。
层次聚类是数据科学中最流行的聚类方法之一，这是有充分的理由的：
- 易于使用，几乎不需要参数调整
- 创建有意义的分类法
- 适用于高维数据
- 不需要事先知道簇的数量
- 每次创建相同的簇
相比之下，像K-Means这样的划分方法则需要数据科学家猜测聚类的数量，非常流行的基于密度的方法DBSCAN则需要围绕密度计算半径（ε）和最小邻域大小的一些参数，而高斯混合模型对潜在的聚类数据分布做出了强有力的假设。
对于层次聚类算法，您只需要指定一个距离度量指标即可使用。
从高级视角来看，层次聚类遵循以下算法：
- 确定所有簇对之间的簇距离（每个簇从一个点开始）；
- 合并彼此最接近的两个群集；
- 重复上述步骤。
结果是：生成一个美丽的树状图，然后可以根据领域专业知识进行划分应用。
在生物学和自然语言处理等领域，（细胞、基因或单词的）簇自然遵循等级关系。因此，层次聚类能够实现对最终聚类截止点的更自然和数据驱动的选择。
下图是著名的鸢尾花（Iris）数据集的层次聚类结果示例。
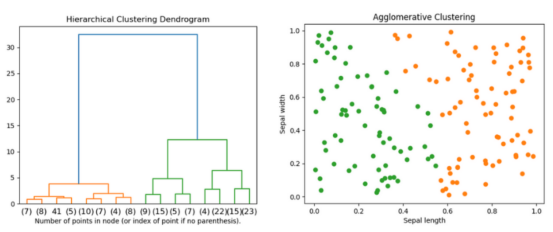
通过萼片长度和萼片宽度对著名的鸢尾花数据集进行聚类（本图表由合著作者Porter Hunley制作）
那么，为什么不对每个无监督分类问题都使用层次聚类算法呢？答案在于：
随着数据集大小的增加，层次聚类算法的运行时间表现得非常糟糕。
另一方面，不幸的是，传统的层次聚类算法还没有得到大规模的应用。如果使用最小堆结构实现的话，则运行时复杂度为O（n³）或O（n²log（n））。更糟糕的是，层次聚类算法在单核的CPU上按顺序运行，无法通过计算进行扩展。
结论是：在自然语言处理领域，层次聚类算法是小型数据集的最佳表现算法。
交互式层次聚类算法
交互式层次聚类（RAC）算法是谷歌提出的一种方法，旨在将传统型层次聚类算法的优势扩展到更大的数据集。
RAC算法降低了运行时的复杂性，同时还将操作并行化以利用多核CPU架构。尽管进行了这些优化，但当数据完全连接时，RAC产生的结果与传统的层次聚类算法却完全相同（见下文）。
注意：完全连接数据意味着，可以计算任何一对点之间的距离度量。非完全连接的数据集则具有连接约束（通常以连接矩阵的形式提供），其中一些点被认为是断开的。请参考下面的对比图示。
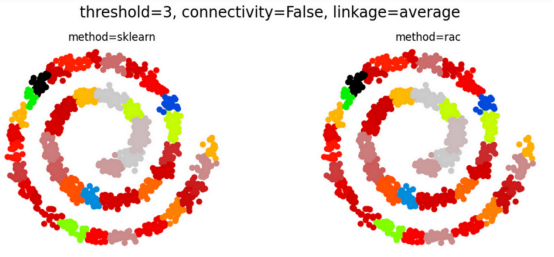
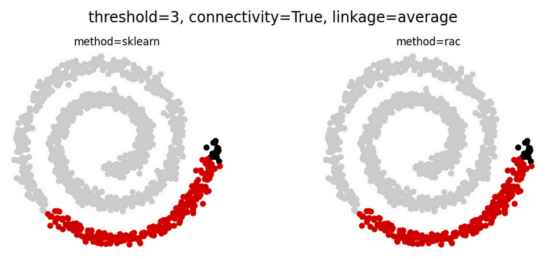
当数据完全连接时，RAC会产生与传统层次群集完全相同的结果！（上图），并且通常在连接约束的情况下继续这样做（下图）（图表由合著作者Porter Hunley制作）
即使存在连接限制（未完全连接的数据），RAC和层次聚类通常仍然相同，如上面的第二个Swiss Roll数据集示例所示。
然而，当可能的簇非常少时，可能会出现巨大的差异。这方面，Noisy Moons数据集就是一个很好的例子：
RAC算法和Sklearn算法之间的计算结果表现出不一致性（本图表由合著作者Porter Hunley制作）
RAC++算法可扩展到比Scikit-learn更大的数据集
我们可以在Scikit-learn中将RAC++算法（交互式层次聚类的一种实现）算法与其对应的层次聚类算法进行比较。
现在，不妨让我们生成一些具有25个维度的示例数据，并使用racplusplus.rac与sklearn.cluster.AglognitiveClustering测试层次聚类需要多长时间，应用于大小从1000到64000点的数据集。
注意：下面代码中，我使用连接矩阵来限制内存消耗。
import numpy as np
import racplusplus
from sklearn.cluster import AgglomerativeClustering
import time
points = [1000, 2000, 4000, 6000, 10000, 14000, 18000, 22000, 26000, 32000, 64000]
for point_no in points:
X = np.random.random((point_no, 25))
distance_threshold = .17
knn = kneighbors_graph(X, 30, include_self=False)
#矩阵必须是对称的：在Scikit-learn库的内部完成
symmetric = knn + knn.T
start = time.time()
model = AgglomerativeClustering(
linkage="average",
cnotallow=knn,
n_clusters=None,
distance_threshold=distance_threshold,
metric='cosine'
)
sklearn_times.append(time.time() - start)
start = time.time()
rac_labels = racplusplus.rac(
X, distance_threshold, symmetric,
batch_size=1000, no_cores=8, metric="cosine"
)
rac_times.append(time.time() - start)以下给出的是每个大小数据集的运行时结果图：
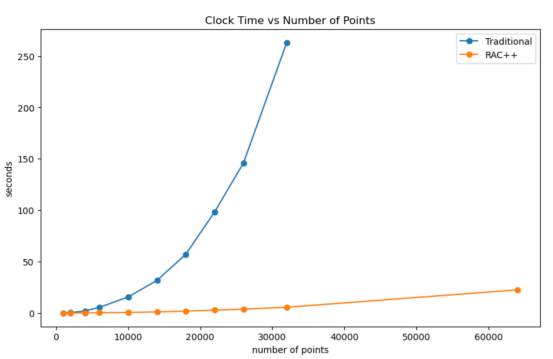
与racplusplus相比，当使用sklearn时，大型数据集的运行时呈爆炸式增长变化趋势（本图表由合著作者Porter Hunley制作）
正如我们从上图中所看到的，RAC++算法和传统的层次聚类算法在运行时有着巨大的差异。
在刚刚超过30k的点上，RAC++算法的速度大约是原来的100倍！更不可能的是，Scikit-learn的层次聚类达到了约3.5万个点的时间限制，而RAC++算法在达到合理的时间限制时可以扩展到数十万个点。
RAC++算法可以扩展到高维度
我们还可以比较RAC++算法在高维数据与传统数据之间的缩放情况。
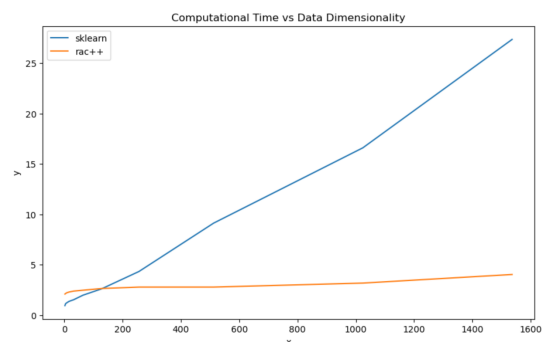
通过RAC++算法和sklearn的数据维度扩展时间复杂性（本图由合著作者Porter Hunley绘制）
上图展示了生成3000点的聚类与维度所花费的时间变化规律。
对于3000点的数据量来说，我们可以看到传统的层次聚类更快，但它是线性的，而RAC++算法表现得几乎是恒定的。如今，使用768或1536维嵌入已经成为NLP领域的常规指标；因此，缩放维度以满足这些要求是很重要的。
RAC++算法表现出具有更好的运行时性能
谷歌的研究人员证明，RAC算法的运行时间为O（nk），其中k表示连接约束，而n代表点的数量——线性运行时间。然而，这不包括初始距离矩阵的计算，即O（n²）——二次运行时。
我们的结果，运行恒定的30个邻连接约束情况下，确实证实了将使用O（n²）复杂度的运行时状态：
+ — — — — — — -+ — — — — — +
| Data points | Seconds |
+ - - - - - - -+ - - - - - +
| 2000 | 0.051 |
| 4000 | 0.125 |
| 6000 | 0.245 |
| 10000 | 0.560 |
| 14000 | 1.013 |
| 18000 | 1.842 |
| 22000 | 2.800 |
| 26000 | 3.687 |
| 32000 | 5.590 |
| 64000 | 22.499 |
+ - - - - - - -+ - - - - - +将数据点增加一倍对应于时间的4倍。
二次运行时限制了RAC++算法在数据集变得真正庞大时的性能，然而，与传统的O（n³）或最小堆优化O（n²log（n））运行时相比，该运行时已经有了很大的改进。
注意：RAC++算法的开发人员正在将距离矩阵作为一个参数进行传递，该参数将为RAC++算法提供线性运行时间。
RAC算法的工作原理
为什么RAC++算法更为快速呢？我们可以将底层算法简化为如下几个步骤：
- 将簇与交互的最近邻配对
- 合并成对的簇
- 更新邻接簇
注意，这与传统的层次聚类算法之间的唯一区别是，我们确保将交互最近邻的簇配对在一起。这就是交互层次聚类（RAC）这个名称的由来。正如您将看到的，这种交互配对使我们能够并行化层次聚类中计算成本最高的步骤。
将簇与交互最近邻配对
首先，我们循环寻找具有交互最近邻的簇，这意味着它们的最近邻是彼此（记住，距离可以是定向的！）。
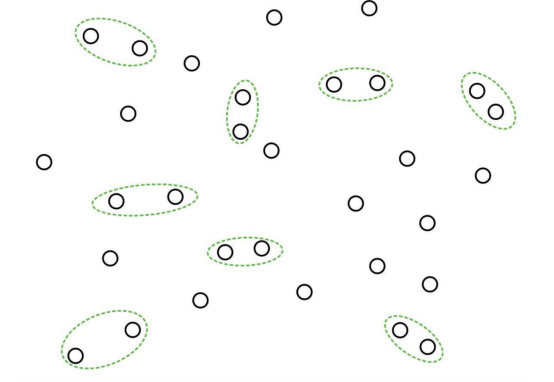识别交互最近邻簇（本图由合著作者Porter Hunley绘制）
合并成对的簇
RAC算法是可并行执行的，因为只要连接方法是可还原的，交互最近邻的合并顺序无关紧要。
连接方法是根据每个聚类中包含的点之间的成对距离来确定两个聚类之间距离的函数。可还原连接方法保证新合并的簇在合并后不会更接近任何其他簇。
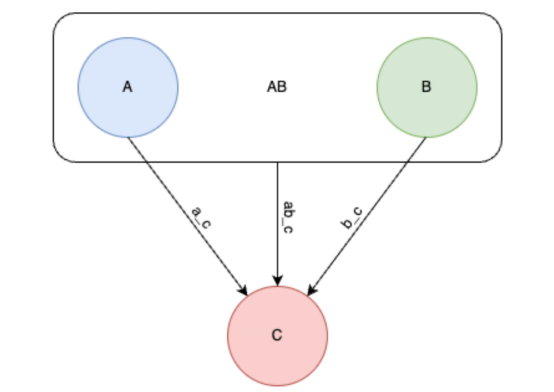
如果使用可还原连接，则ab_c将不会比ac或bc更接近（此图由合著作者Porter Hunley绘制）
幸运的是，四种最流行的连接方法都是可还原的：
- 单连接——最小距离
- 平均连接——距离的平均值
- 完全连接——最大距离
- 离差平方和法连接——最小方差
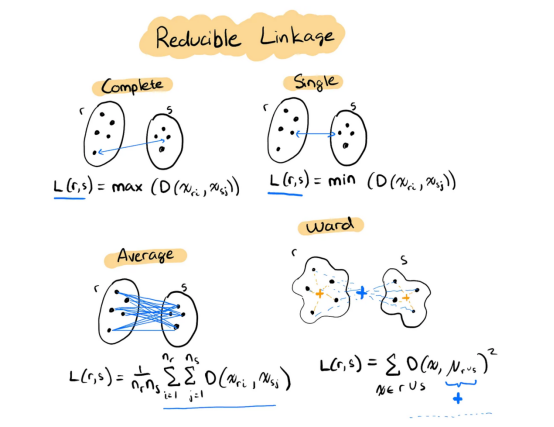
4种可还原连接方法的可视化表示（我本人绘制，灵感来自http://www.saedsayad.com/clustering_hierarchical.htm）
由于我们知道我们识别的交互对是彼此的最近邻居，并且我们知道可还原连接合并永远不会使新合并的簇更接近另一个簇，因此我们可以安全地将所有交互最近邻居对同时合并在一起。每个最近邻居对可以被放置到一个可用线程中，以便根据连接方法进行合并。
我们可以同时合并交互最近的邻居，这一事实非常棒，因为合并簇是计算成本最高的步骤！
可视化准备合并的簇（本图由合著作者Porter Hunley绘制）
更新最近邻簇
对于可还原连接，合并后更新最近邻的顺序也无关紧要。因此，通过一些巧妙的设计，我们也可以并行地更新相关的邻居。
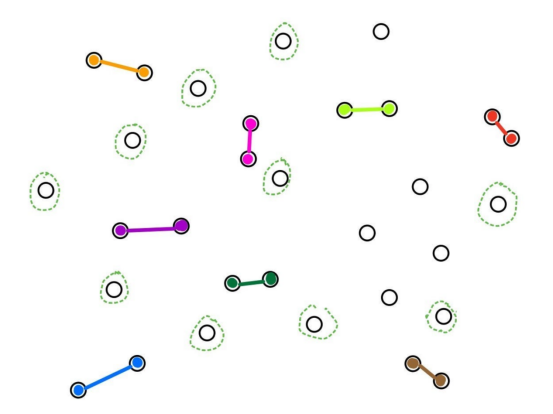在合并后识别新的最近邻簇（本图片由合著作者Porter Hunley绘制）
结论
通过一些测试数据集，我们已经表明，对于完全连接的数据集，RAC++算法在更好的运行时产生与传统的层次聚类算法（即sklearn中所提供的）完全相同的结果。通过对可还原连接度量指标的解释和对并行编程支持的基本分析，我们最终理解了使RAC++算法更快的逻辑。
为了更完整地理解（和证明）RAC++算法在开源包中所采用的算法，有兴趣的读者可以查看它所基于的谷歌原始研究成果。
未来的工作
目前，Porter Hunley已经开始构建RAC++算法，努力为通过微调BERT嵌入产生的临床术语端点创建分类法支持。这些医学嵌入中的每一个都有768个维度，在他尝试的许多聚类算法中，只有层次聚类算法给出了良好的结果。
所有其他的高规模聚类方法都需要降维才能给出任何连贯的结果。不幸的是，当前还不存在一种很有把握的方法用于降低维度——你总是会丢失一些信息。
在发现谷歌围绕RAC的研究成果后，波特决定构建一个自定义的开源簇实现，以支持他的临床术语簇研究。Porter负责开发，我和他共同开发了RAC算法的一些部分，特别是在python中封装C++实现，优化运行时，以及打包软件以供分发方面。
总之，RAC++算法支持大量簇应用程序，这些应用程序使用传统的层次聚类表现得太慢，最终将扩展到数百万个数据点。
最后，尽管RAC++算法现在已经可以用于簇式大型数据集，但仍存在不少有待改进之处……RAC++算法仍在开发中！
本文特约作者：
- Porter Hunley，Daceflow.ai高级软件工程师：他的GitHub代码仓库是https://github.com/porterehunley
- Daniel Frees，斯坦福大学统计与数据科学硕士生，IBM数据科学家：他的github代码仓库是https://github.com/danielfrees
注：GitHub——porterehunley/RAPlusplus：交互聚集的高性能实现……
译者介绍
朱先忠，51CTO社区编辑，51CTO专家博客、讲师，潍坊一所高校计算机教师，自由编程界老兵一枚。
原文标题：Scaling Agglomerative Clustering for Big Data，作者：Daniel Frees
