背景
作为长链条严格推理的典范,数学推理被认为是衡量语言模型推理能力的重要基准,GSM8K 和 MATH 等数学文字问题(math word problem)数据集被广泛应用于语言模型的测评和比较中。事实上,数学作为一项科学研究并不仅仅包括计算具体实例,还包括推演一般性的定理。不同于简单的计算问题仅仅需要验证最终的结果与答案是否匹配,定理的证明要求对数学概念拥有更严格的理解,而这种定理证明的正确性是难以通过直接的自然语言生成和判别或是简单的程序调用就能够完成的。
正如自然语言处理希望能够使用计算机直接对人类语言进行数字化计算一样,对于数学对象的数字化也有着数十年的探索,甚至现代形式逻辑的诞生在很大程度上也正是源于对数学命题进行演算的想法。从事形式化验证的计算机科学家致力于为数学论述构造表达自然且计算高效的形式语言和证明验证器,人工编写的形式化数学代码在通过计算机的形式化验证后被认为具有高度的严格性。然而,这一过程需要大量的人工成本,著名的 Flyspeck project 甚至花费了二十年的时间才完成开普勒猜想的证明,而自动化的证明搜索算法则面临着搜索空间的组合爆炸问题,导致非平凡的定理证明往往超出了当前的计算能力限制。
深度学习的发展为形式化数学和自动定理证明提供了新的机遇。近年来,一种名为神经定理证明(neural theorem proving)的新范式以两种方式尝试将神经网络与形式定理证明相结合:使用神经网络对数学库中的定理和当前的证明目标分别进行向量表征并进行匹配,筛选出最可能被使用的定理,帮助纯符号计算的自动定理证明器缩小证明搜索空间;或者将证明目标作为提示输入语言模型,使其直接生成相应的形式化数学证明代码,再使用相应的形式化验证器来判断该证明的正确性,这种直接代替人类编码者完成主要证明内容书写的直接模式在大语言模型取得突破后备受关注。
然而,与数学文字问题一样,当前进行定理证明的方法通常是 “一次性的”,也即推理过程和中间结论仅仅作为通向最终证明的临时性路径,在完成证明的验证后即被丢弃、并不对后续的定理证明产生贡献。这种方式更像是对大语言模型进行静态测试,而没有对其能力的持续提升做出贡献。
事实上,数学的发展并不仅仅是简单的重复尝试解题,还包括从实例中「抽象」出普遍的数学结构和定理、从特殊的定理推广到一般的定理和根据已有的定理演绎地「推出」新的结论。
随着这一过程的演进,数学家对更复杂的问题拥有更强大的工具和更深刻的理解,最终才能解决先前无法解决的困难问题。
为了解决这一问题,模拟人类数学家在进行定理证明时通常进行的分解复杂问题、引用已有知识,并积累成功证明的新定理的迭代过程,中山大学和华为等机构的研究者提出了 LEGO-Prover,实现了数学定理的生成、整理、储存、检索和复用的全流程闭环。
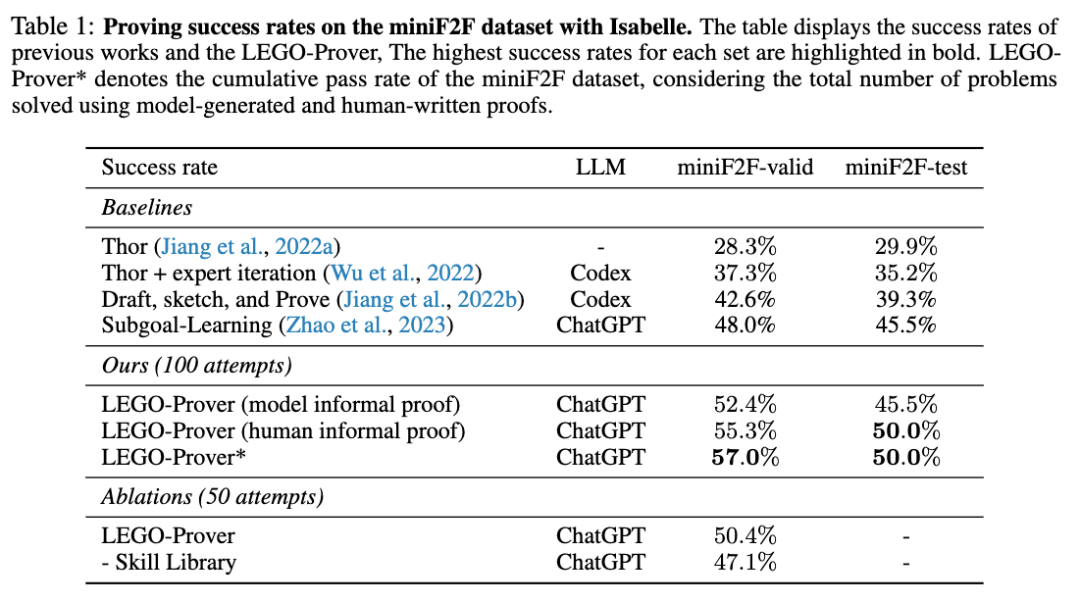
LEGO-Prover 使 GPT-3.5 在形式化定理证明数据集 miniF2F-valid(证明成功率从 48.0% 提高到 57.0%)和 miniF2F-test(证明成功率从 45.5% 提高到 50.0%)上都达到了新的 SOTA。在证明过程中,LEGO-Prover 还成功地生成了超过 20,000 个引理并将它们添加到了不断增长的定理库中。
消融研究表明,这些新添加的技能确实对证明定理有帮助,在 miniF2F-valid 上的证明成功率从 47.1% 提高到 50.4%。

- 论文地址:https://arxiv.org/abs/2310.00656
- 代码地址:https://github.com/wiio12/LEGO-Prover
方法

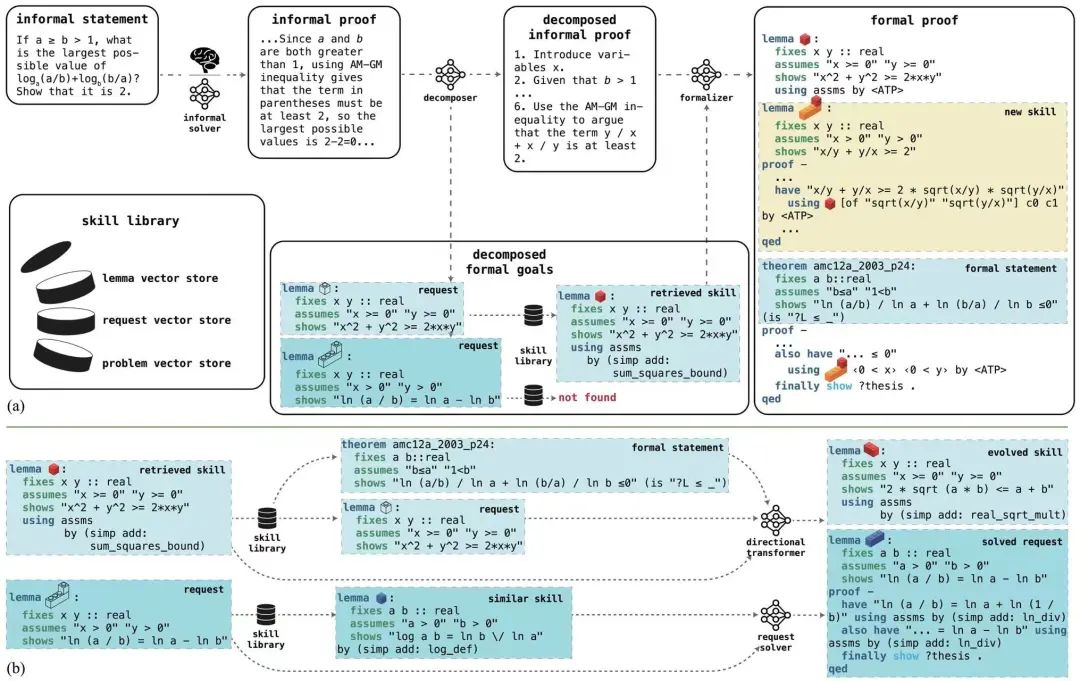
LEGO-Prover 采取了一系列的流程来实现对定理证明的规划、实施和可复用定理库的收集:
1. 给定一个以自然语言描述的数学定理及其人类编写的形式化描述,使用 GPT-3.5(informal solver)直接生成的自然语言证明。
2. 使用分解器(decomposer)将这一自然语言证明分解为具体的证明步骤,并以引理的形式对这些证明步骤中的子目标进行对应的形式语言描述(作为检索的 request)。
3. 利用这些以形式语言描述的子目标尝试从定理库(也即 skill library)中检索相关的已证明定理,将其与上述内容一同输入 GPT-3.5(formalizer),在这些提示的基础上进行目标定理的形式化证明,并使用形式化验证器检验证明的正确性。
4. 从通过验证的形式化证明中,提取出除目标定理外的其他通过验证的定理(或引理)和在分解过程后得到的子目标形式语言描述,对它们进行 embedding 后加入到维护的定理库中。
此外,LEGO-Prover 还对定理库进行了专门的整理和维护流程,对分解过程中收集到的子目标进行单独的证明尝试,通过多种类别的 prompt 引导 GPT-3.5 对证明过程中收集到的成功证明的定理进行演化,从具体的证明实例抽象出一般的数学命题,以增进定理库中命题的多样性、概括性和可复用性:

实验
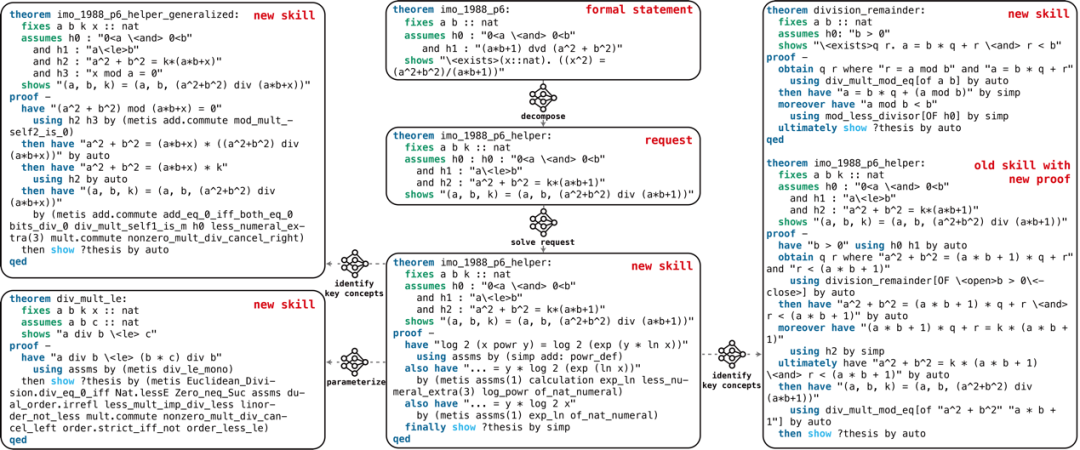
实验表明,这些演化得到的新定理在后续的定理证明中起到了关键性的作用,miniF2F 数据集中的许多定理都是在利用这些从定理库中抽取得到的结果才得以证明的。使用收集和演化得到的定理库后,LEGO-Prover 的证明成功率从 47.1% 提高到 50.4%,而在使用定理库的情形下,有 24% 的问题是在技能库的帮助下完成的,这表明技能库的使用对于大语言模型进行定理证明任务而言帮助很大。此外,使用定理库技术的优势在较小的尝试次数下具有较高的比例,表明这一方法对于计算资源相当有限的情形下具有相当可观的使用价值。
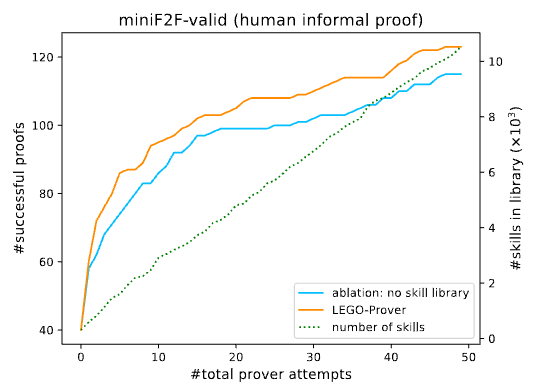
最后,实验结果表明 LEGO-Prover 在 miniF2F 数据集上的证明成功率显著优于基于先前的方法。使用人类编写的证明,LEGO-Prover 在验证集和测试集上的证明成功率分别比先前最好的方法高出 19% 和 3.5%。当使用模型生成的非正式证明替代人类编写的非正式证明时,LEGO-Prover 在验证集上的证明成功率仍然达到了 52.4%,接近于使用人类编写的非正式证明的证明成功率 55.3%。
LEGO-Prover 探索了如何以块状的方式证明定理。然而数据稀缺问题在定理证明这个领域内依旧非常严重。因此,与此同时,中山大学联合北京大学还推出了基于三角函数的定理证明基准数据集 TRIGO (https://arxiv.org/abs/2310.10180),发表于EMNLP 2023。
TRIGO 对自动引理生成以及如何从合成的引理数据的分布泛化到真实世界数据的分布进行了进一步的探索。当前的自动定理证明数据集主要侧重于符号推理,很少涉及复杂数字组合推理的理解。TRIGO 不仅要求模型通过逐步证明来简化三角函数表达式,还评估了生成式语言模型在公式和数字术语的操作、分组和因式分解方面的推理能力。研究团队从网络上收集了三角函数表达式及其简化形式,人工标注了简化过程,然后将其转化为 LEAN 形式系统下的语言。在有一定的来自于真实世界的形式化定理数据后,研究团队利用引理生成器,从已标注的样本中初始化 Lean-gym 来自动生成新的引理以扩展数据集。
此外,TRIGO 还开发了基于 lean-gym 的自动生成器,用以创建不同难度和分布的数据集拆分,以全面分析模型的泛化能力。TRIGO 在定理证明领域提供了新的挑战,同时也提供了一种研究生成式语言模型在形式和数学推理方面能力的新工具。

此外,为了探索定理证明模型的能力在更难的数据集上的表现,中山大学联合北京大学还提出了 FIMO 基准数据集(https://arxiv.org/abs/2309.04295)。形式化数学数据稀缺,手工形式化成本非常高昂。当前主流的数据集主要聚焦于初高中水平的应用题,难度普遍偏低,对于 IMO 等需要高水平解题技巧的数学竞赛题目关注较少,而且常常不包括自然语言题解。
针对现有数据集的问题,FIMO 探索了使用反馈信息的自动形式化方法,使用 GPT-4 和自动、手动两种反馈信息,将数量较为丰富的 IMO Shortlisted 候选题转换为了 Lean 语言描述的形式语言。
实验结果表明,反馈机制的加入大大缓解了先前自动形式化的语法错误和语义错误,显著提升了自动形式化的成功率(32.6%→60.8),成功形式化了 89 道代数和 60 道数论的高难度题目。进一步的实验表明,虽然 GPT-4 无法直接生成 IMO 级别题目的形式化题解,但是它可以跟随自然语言答案的解题思路,暗示了使用自然语言辅助机器定理证明的可能性。