马斯克的xAI,首项公开研究成果来了!
共同一作之一,正是xAI创始成员、丘成桐弟子杨格(Greg Yang)。
此前,杨格就曾公开表示,自己在xAI的研究方向是“Math for AI”和“AI for Math”。
其中一项重点就是延续他此前的研究:
描述神经网络架构的统一编程语言Tensor Programs——相关成果,在GPT-4中已有应用。
这次的新论文,就归属该系列,重点探讨了“如何训练无限深度网络”。

为此,杨格本人还专门在𝕏上进行了一场直播分享。
一起来看看有哪些精彩内容值得mark~
训练无限深度神经网络
简单来说,这篇文章研究的是残差网络(ResNet)在深度方向的扩展。
我们知道,残差网络解决了深度增加时,深度卷积神经网络性能退化的问题。但当网络继续加深,训练一个好的深度残差网络仍非易事:
当网络加深时,特征的规模会不断增大,导致网络不稳定;加深网络后,需要重新调整超参数,工作量不小……
杨格和他的小伙伴们的想法是,找到一种深度参数化方法,既可以学习特征,又可以实现超参数迁移。
他们首先想到了无限宽神经网络存在的两种极限情况:要么是核机(kernel machines),要么是特征学习器(feature learners)。对于后者而言,最佳超参数是不会随宽度变化而变化的。
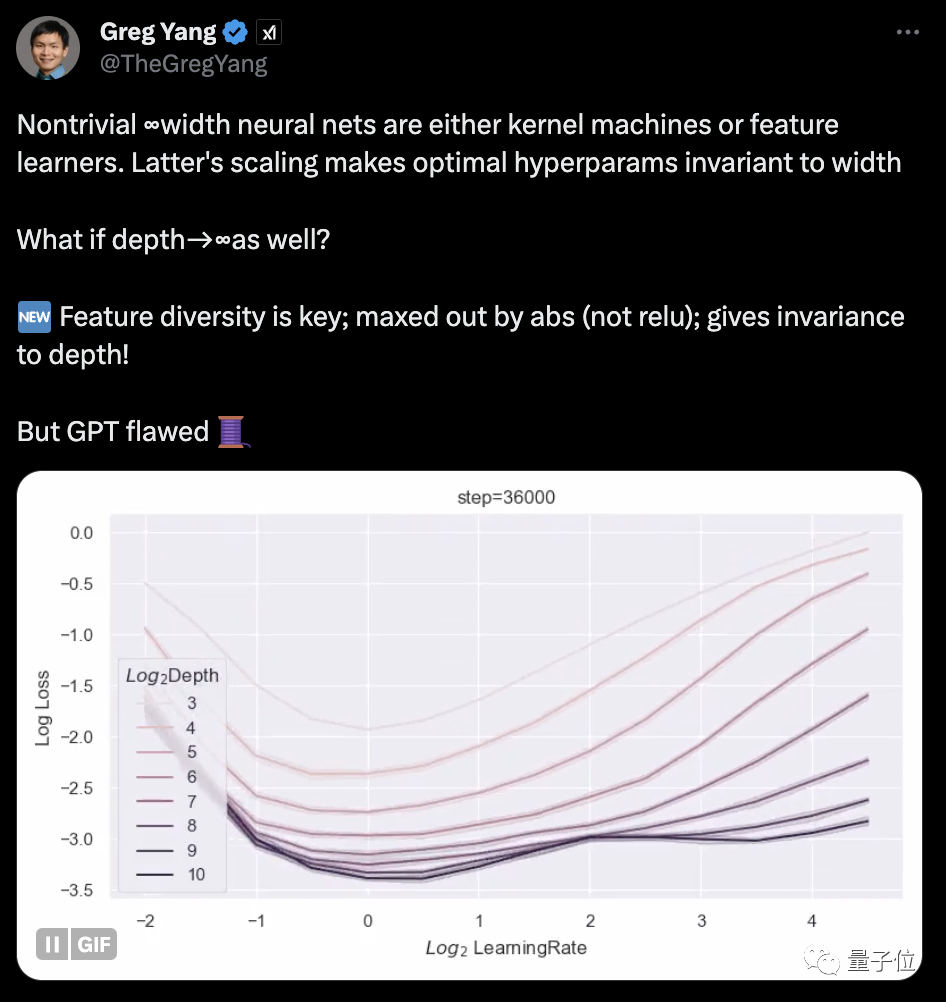
在这里,他们使用Tensor Programs框架分析了无限宽网络的极限情况。
正如前文提到的,Tensor Programs是杨格的一项长期研究目标:用数学语言,建立能够描述和分析神经网络架构的底层编程语言。
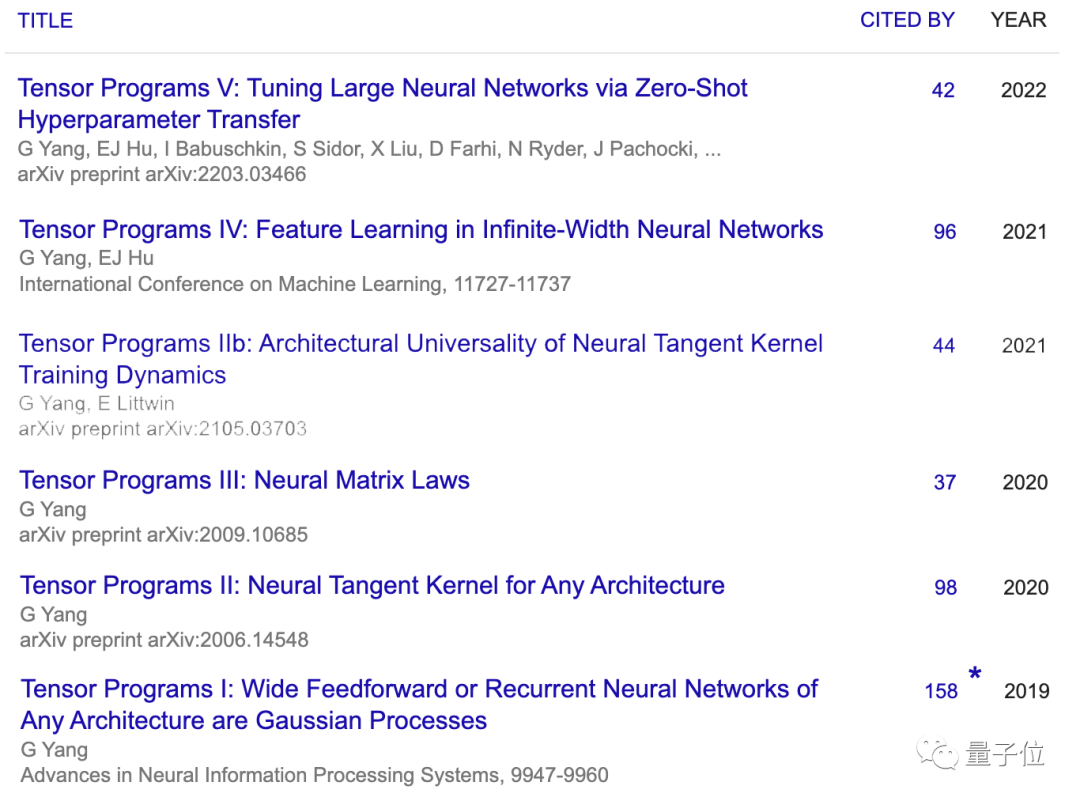
具体而言,Tensor Programs由矩阵乘法和激活函数组成。杨格发现,如果神经网络函数能够使用这种语言表达,就可以自动且完备地进行初始化分析。
数学推导的部分,这里不做具体展开,我们可以浅浅感受一下画风……

在这些推导分析的基础之上,作者提出了Depth-μP方法,可以实现深度方向上的超参数迁移,大大简化了不同深度下的超参数调节。
Depth-μP包含以下要点:
- 每个残差分支和深度L的平方根成反比的系数a/sqrt(L)。
- 每个权重矩阵的学习率随深度L变大而减小,具体取决于优化算法的类型。对于SGD,学习率取常数η,对于Adam等自适应优化算法,学习率取η/sqrt(L)。
值得关注的是,作者发现,当残差块深度为1时,Depth-μP是深度参数化的最优方式,可以保证超参数随着深度的增加而收敛,实现深度方向的超参数传递。
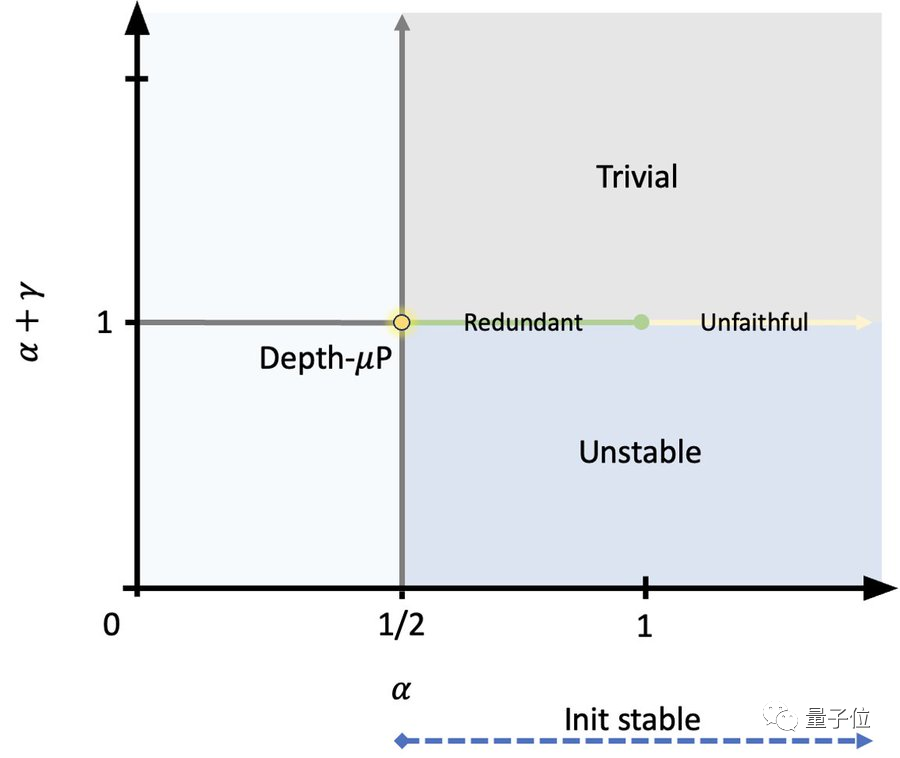
但当残差块深度≥2时,还是会出现超参数迁移失败和训练性能下降的问题。
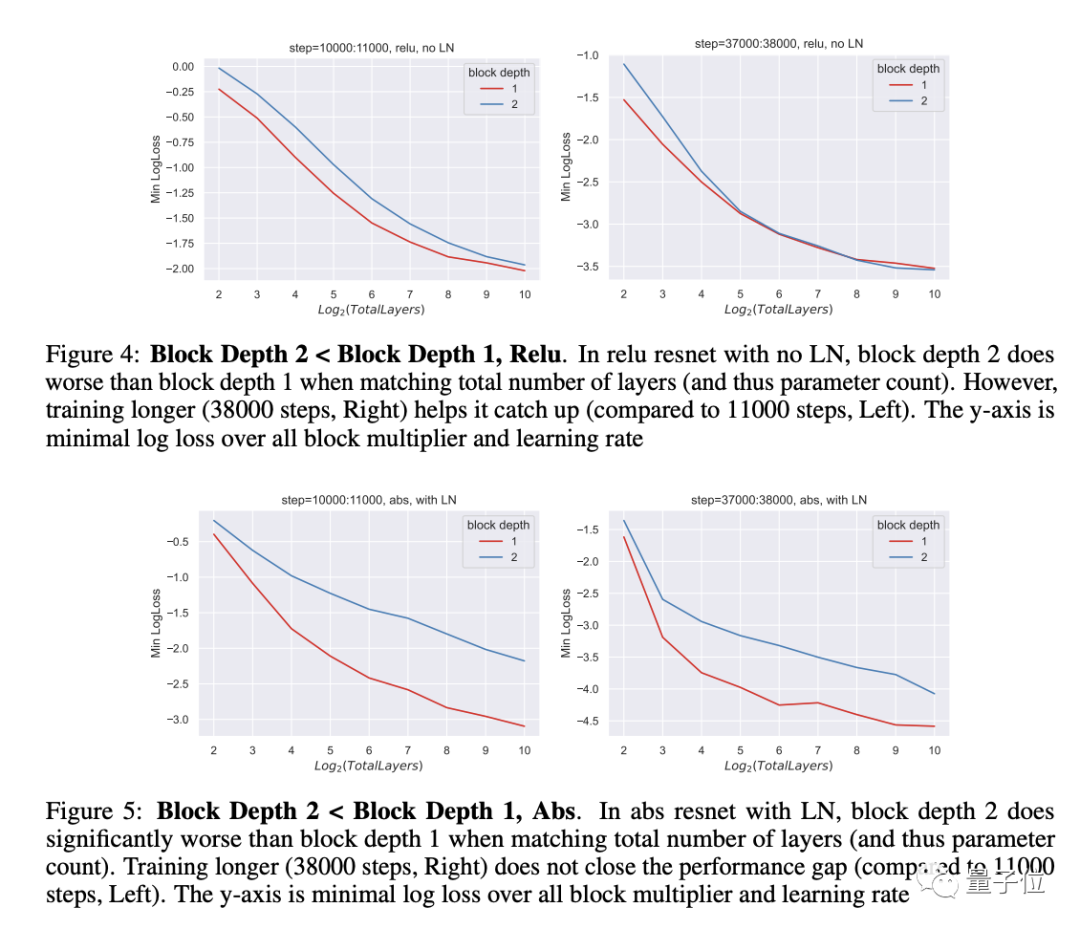
另外,论文还探讨了“特征多样性”的概念,认为它在深度网络中发挥着关键作用。
论文的另一位共同一作是来自普林斯顿的Dingli Yu。他本科毕业于清华姚班,目前在普林斯顿计算机科学系攻读博士。
杨格在直播中都说了啥?
在直播中,杨格还就观众感兴趣的问题进行了解答。在不改变原意基础上,量子位对部分问题做了梳理。
Q:对于我们许多人来说,(论文内容)可能超出了我们的理解范围。但我想知道,你提到的模型与我们能够体验到的ChatGPT以及OpenAI的技术有何不同?这篇论文与OpenAI的成果相比有什么显著的差异或是创新点?
杨格:我简单评论一下,我想说这些特性目前与实际应用并没有直接关系,更像是研究性质的。
当然,做这一切的最终目标是为了让模型更好、更安全,然后造福人类。我们现在所进行的是描述预期的效果,它不一定会有直接的影响。
现在我们同处一条船上,我们正在做我们所能做的事,无论是短期工作还是长期应用研究,都是为了让它造福每个人。
Q:听起来像是你们正在建造一个能够进行推理的人工计算机大脑,所以这是你们正在研究的吗?此外,我还是一位母亲,我7岁的儿子对数学非常感兴趣,你有什么可以让他继续对AI领域保持兴趣和热情的建议吗?
杨格:“新型网络”指的是人工神经网络,我认为它是现代众多技术的支柱,包括您每天使用的Google、Facebook、Instagram等,这些服务的底层都使用了这些人工神经网络。这些网络大约在六七十年前受到动物、人类的真实神经网络启发而诞生,但已与真实的神经科学有所偏离。
这些网络本质上是数学问题,因此我们掌握这些新的数学问题后进行大量分析,可以深入地理解这些神经网络。
虽然我们尚不明确真正的神经元的连接方式,但通过数学研究,我们能优化这些人工神经网络,助力科技公司改善人们的生活。
关于您的第二个问题,听说您的儿子对数学非常感兴趣,这太棒了。这是在技术领域创造伟大成就和改善每个人生活的基础。
我想给的建议是,首先您要保持您儿子对数学的热情,这非常重要。一旦失去了这份热爱,想再继续学习就会变得很困难。
还要注意观察他喜欢的东西,让学习过程变得有趣,进一步激发他的兴趣。同时,也要培养他对事物运作原理的好奇心,并尝试培养一种科学思维,要在好奇心的驱使下研究。就像拆解事物,尝试理解它们的工作原理。
如果一个人失去了对宇宙数学真理的探索热情,可能很难再有前进的动力。总的来说,我建议您培养您儿子对这个世界,特别是对数学和科学本质的浓厚兴趣和好奇心。
Q:我有一个更为抽象的问题。你有了深度趋近于无穷的想法,然后根据这种想法写了这篇论文。那你是否考虑过采用不同架构的神经网络?不是带有神经元和无数层的标准架构,而是完全不同的东西。比如这些神经元的连接方式完全不同,也许是某种正方形?
杨格:其实关于非线性以及我们这项工作中对层数的洞察,都只是非常初级的研究。关于什么是合适的结构,或者应该是怎样的结构,当然还有很多可以探讨的问题。
像Meta团队之前就研究了随机连接神经元会发生什么,得到了一些有趣的结果。所以,这里绝对还有很多可以做的事情。现在我确实没有具体的答案来说什么将是正确的或者更好的结构。
关于杨格
杨格出生于湖南省,小学毕业后去了美国,本科就读于哈佛师从丘成桐教授。
△杨格与丘成桐,图源:杨格推特
2017年,杨格哈佛毕业,之后在沈向洋引荐下进入微软。
在微软,杨格获得了沈向洋的高度评价。几个月前,在一场名为“基础科学与人工智能”的论坛上,沈向洋公开表示:
微软研究院平时只招博士生的,杨格作为一个本科毕业生进了微软研究院。不仅进了微软研究院,过去这五年还做得无比优秀,特别是在GPT发展过程中做了举足轻重的贡献。
值得一提的是,他本人也曾承认GPT-4就用到了他的μTransfer(Tensor Programs系列)方法。
而杨格对Tensor Programs的研究,从很早就开始了,2019年就发表了“Tensor Programs I”,在微软工作时也是持续深入探索。他认为深度学习中几乎任何计算都可以表示为Tensor Programs。
今年7月,马斯克宣布成立新公司xAI,杨格离开微软,加入xAI创始团队,成为xAI的数学家。
加入xAI后,杨格不止一次透露Tensor Programs项目长期目标是开发大规模深度学习的“万物理论”,也就是找到一种理论上的规则,可以真正理解AI大模型的行为。
他还表示:
AI将使每个人都能以此前难以想象的方式理解我们的数学宇宙。
论文链接:https://arxiv.org/abs/2310.02244











































