Java代码手撕【数据结构】| 队列的实现与优化指南

一、前言

队列是一种重要的数据结构，它按照“先入先出”（FIFO）的原则管理数据。本文将介绍队列的概念、应用场景，以及如何使用数组实现普通队列和环形队列。

二、内容

2.1 概述

2.1.1什么是队列？

队列（Queue）是一种常见的数据结构，它是一个线性数据结构，按照先入先出（FIFO，First-In-First-Out）的原则来管理数据。

注意，先入先出的原则就意味着最早进入队列的元素将最先被取出，而最后进入队列的元素将最后被取出，类似于排队等候服务的行为。

队列可以使用数组或链表来实现，具体实现方式因应用需求而异。

队列支持两种主要的操作，即入队（Enqueue）和出队（Dequeue）。

• 入队：将元素添加到队列的尾部。
• 出队：从队列的头部取出元素并删除它。

应用场景

队列的应用场景有很多，比如：

1. 任务调度：操作系统使用队列来管理待执行的任务或进程，确保按照进入队列的顺序分配处理时间。
2. 数据缓冲：队列用于数据传输和处理中，特别是在异步通信或生产者-消费者模式中，可以缓冲待处理的数据。
3. 广度优先搜索：在图论和搜索算法中，队列用于实现广度优先搜索，以逐层遍历图结构。
4. 打印任务队列：打印机队列用于管理待打印的文档，确保按照顺序打印。
5. 网页请求队列：Web服务器可以使用队列来处理收到的请求，以便有序响应客户端请求。
6. 排队系统：在银行、餐馆、医院等场所，队列被用来管理等待服务的客户，确保服务按照先来先服务的原则。
7. ......

队列在计算机科学和实际应用中非常有用，因为它们提供了一种有效的方法来管理和调度数据或任务，以确保按照特定的顺序进行处理。

2.2 数组模拟队列

下面，我们用数组来模拟一个简单的队列数据结构。

2.2.1 队列类定义

首先给出类的定义：

class ArrayQueue {
    private int maxSize;
    private int front;
    private int rear;
    private int[] data;
    
    ArrayQueue(int queueMaxSize) {
        maxSize = queueMaxSize;    // 队列的最大容量
        data = new int[maxSize];    // 存放队列的数据
        front = -1;    // 指向队列头的前一个位置
        rear = -1;     // 直接指向队列尾部
    }
	
    // ... 方法定义
}

在这里，ArrayQueue 是一个队列类，使用数组作为内部数据存储。它包括最大容量（maxSize）、队列头（front）、队列尾（rear）和一个整数数组（data）来存放队列的数据。

构造函数 ArrayQueue 接受一个整数参数 queueMaxSize，表示队列的最大容量。初始化时，队列的头（front）和尾都（rear）被置为-1，表示队列为空。

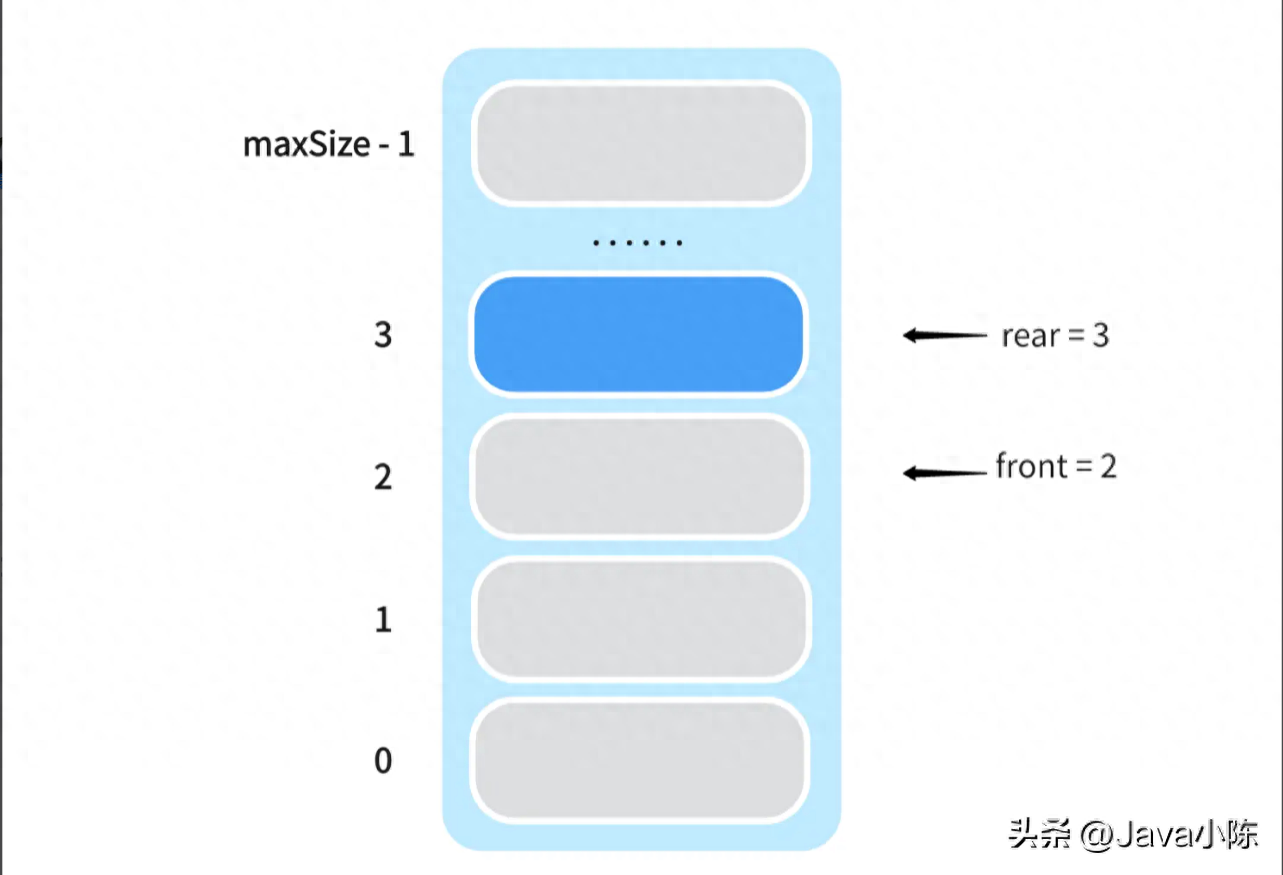
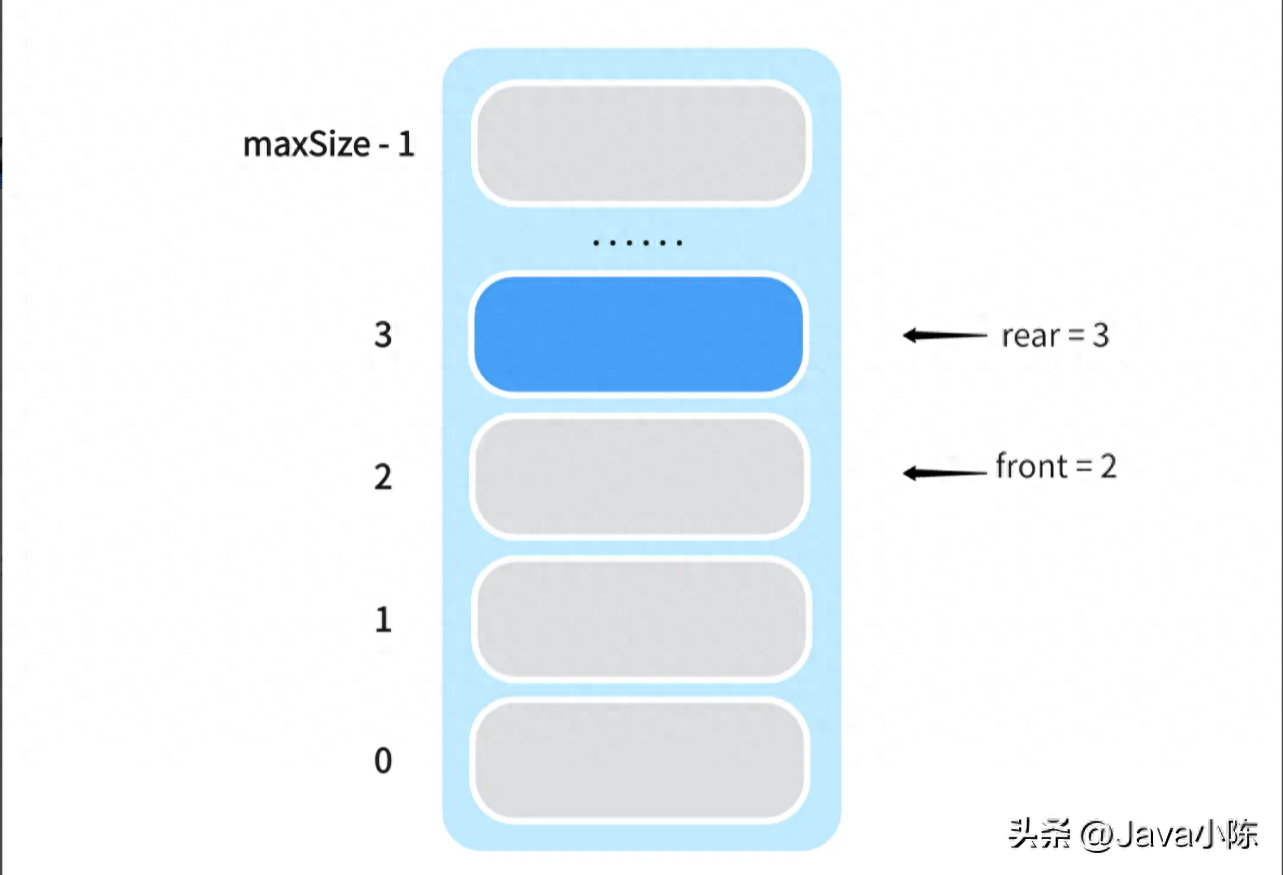
需要注意这里的定义，在这里，front 变量指的是指向队列首元素的前一个位置，而 rear 变量则指向队列的尾部元素，即最后一个元素。

因此，初始队列的结构图如下：

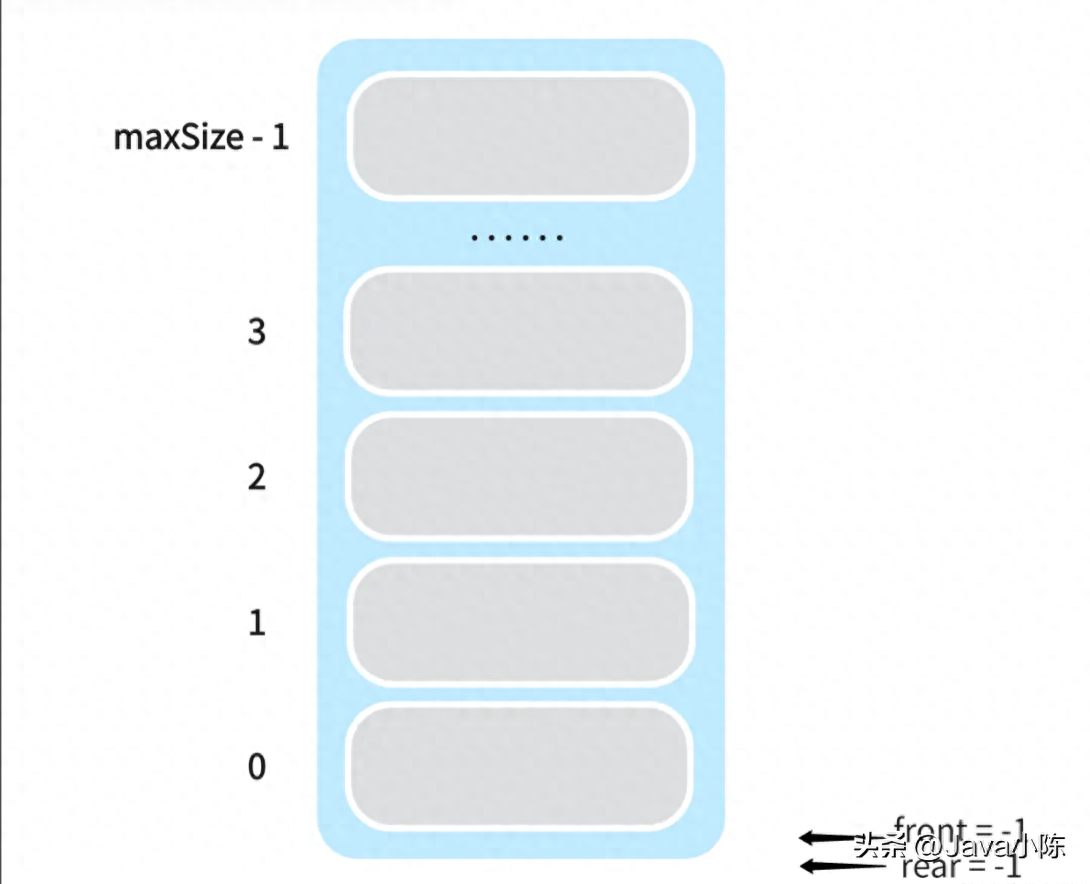
2.2.2 isEmpty

public boolean isEmpty() {
    return rear == front;
}

2.2.3 isFull

public boolean isFull() {
    return rear == maxSize - 1;
}

2.2.4 enQueue

// 入队操作，添加数据到队尾
public void enQueue(int num) {
    if(isFull()) {
        System.out.println("队列已满，无法入队");
        return;
    }
    rear++;
    data[rear] = num;
}

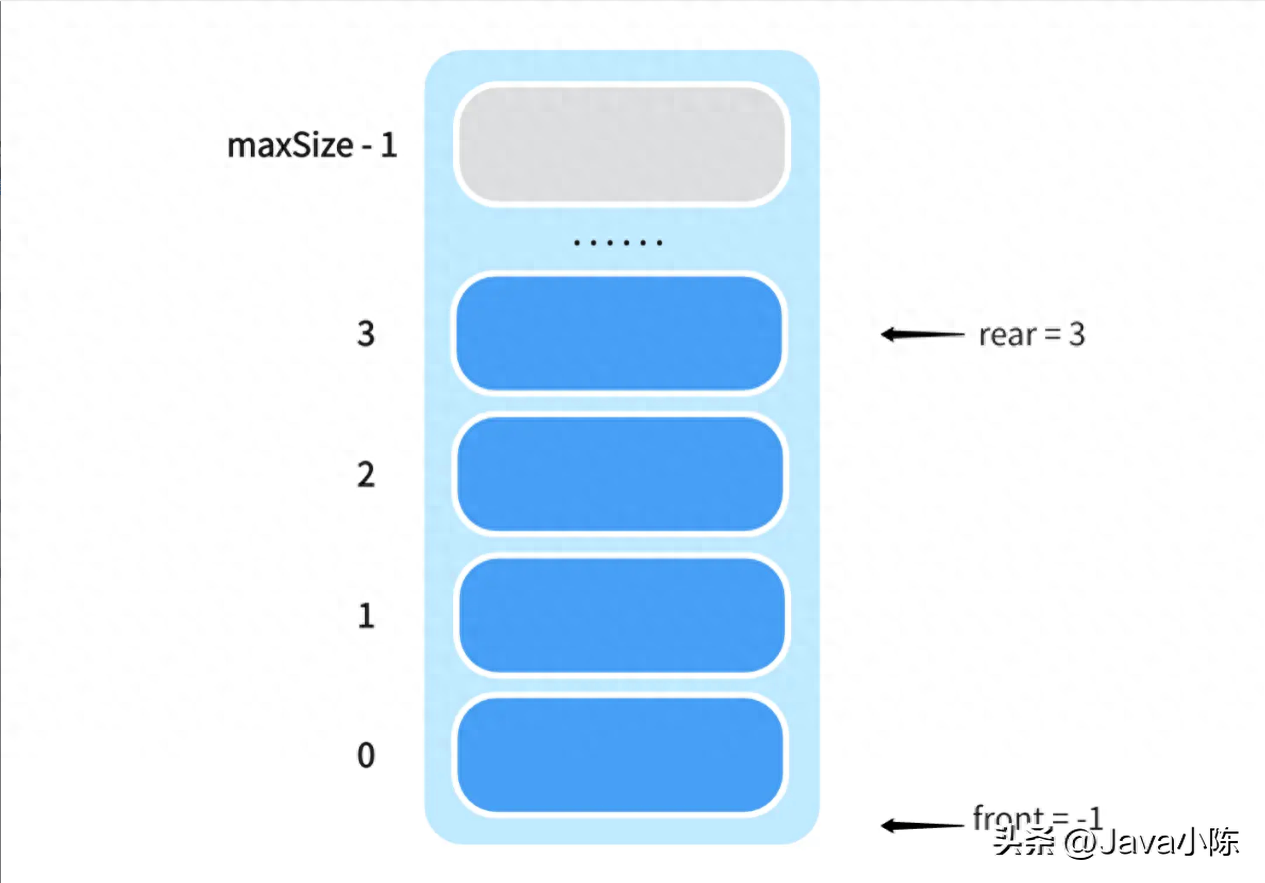
enQueue 方法用于将数据添加到队列的尾部。首先，它会检查队列是否已满，如果是，将输出一条错误消息并不执行入队操作。如果队列未满，将 rear 后移，然后将数据存入队列尾部。

再次强调一下，这里的 rear 变量用于指向队列的最后一个数据，即队列的尾部。

2.2.5 deQueue

// 出队操作，取出队头数据
public int deQueue() {
    if(isEmpty()) {
        throw new RuntimeException("队列为空，无法出队"); 
    }
    front++;
    return data[front];
}

deQueue 方法用于取出队列头部的数据。首先，它会检查队列是否为空，如果是，将抛出一个运行时异常。如果队列不为空，将 front 后移，然后返回队头的数据。

再次强调一下，这里的 front 变量指向的是队列头数据的前一个位置。

2.2.6 headQueue

// 查看队头数据（注意不是取出数据）
public int headQueue() {
    if(isEmpty()) {
        throw new RuntimeException("队列为空，没有数据");
    }
    return data[front+1];
}

headQueue 方法用于获取队列头部的数据，但不会将其出队。它会检查队列是否为空，如果是，将抛出一个运行时异常。如果队列不为空，将返回队头的数据。

2.2.7 showQueue

// 打印队列
public void showQueue() {
    if(isEmpty()) {
        System.out.println("队列为空，没有数据");
        return;
    }
    // 简单的遍历队列
    for(int i = 0; i < data.length; i++) {
        System.out.printf("data[%d] = %d\n", i, data[i]);
    }
}

showQueue 方法用于简单地打印队列的所有元素。如果队列为空，将输出一条消息表示队列为空。否则，它会简单地遍历队列，打印每个数据元素的索引和值。

2.3 数组模拟环形队列

存在的问题

我们再来思考一个问题，虽然上述的队列类实现了一个简单的队列数据结构，但仍然存在弊端。那就是数组使用一次后不能复用。

什么意思？

具体的，我们可以发现，每当队列入队一个数据，rear 变量就会往后移一位。每当有元素出队，front 变量也会往后移一位。但是！一旦 rear 变量到达队列的尾部，如果队列头部仍有空余的空间，就像这样：

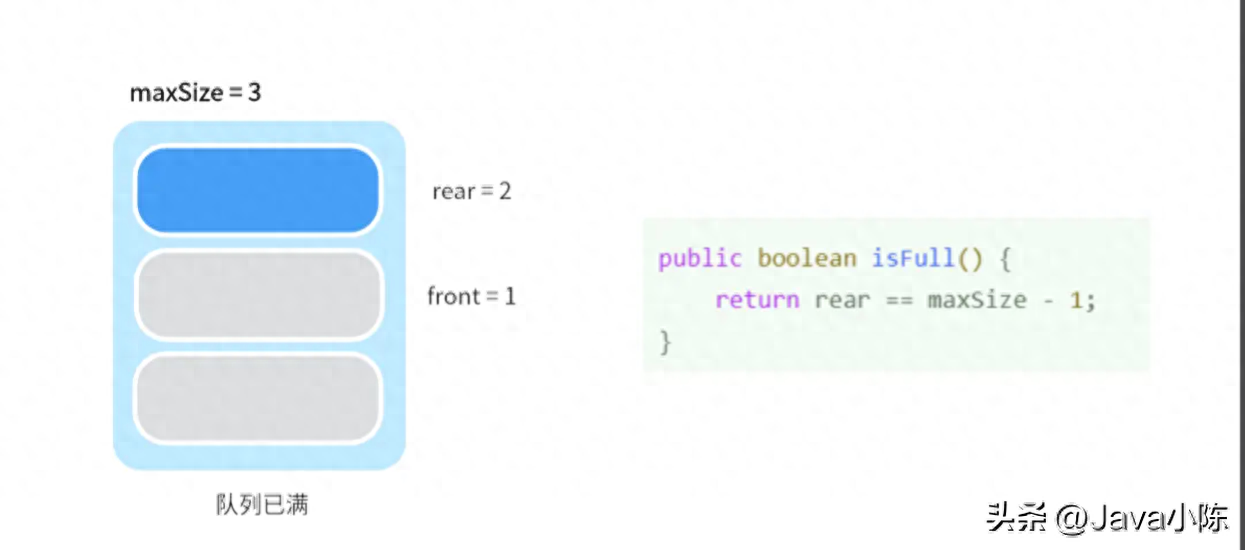
那么此时根据 isFull() 方法的判断下，该队列是满的。因此无法再入队。

因此我们说，对于之前的队列简单实现来说，一旦队列中的数据元素被取出，对应的数组位置就不能再次使用。数据从头部添加，从尾部取出。一旦数组被填满，我们无法再添加新的数据，即使队列的前面已经有一些位置被释放出来。这就会导致内存资源浪费。

为了解决这个问题，我们考虑使用环形队列来优化。

那什么是环形队列？

事实上，环形队列是一种更高效的队列实现方式，它允许队列在达到最大容量后继续添加元素，以覆盖掉队列头部已经被取出的数据，实现数据的循环复用。

我们通过取模运算 % 来实现环形队列。

思路分析

当我们考虑了队列内部数据存储资源的复用后，我们就需要对 front 和 rear 变量的含义进行一个的调整（当然不调整也行，看个人习惯）。

具体如下：

• front 变量： 表示指向队列的第一个元素，即首元素。 data[front] 是队列的第一个元素。 front的初始值为 0。
• rear 变量： 表示指向队列最后一个元素的下一个位置。 这是为了表示队列中哪些位置是可用的，以便继续添加新的元素。 rear 的初始值同样为 0。

当我们这样约定好了后，就可以开始着手编写代码，得到一个环形队列。

此时判断队列已满或空时，逻辑需要略微调整。

判断环形队列空时，条件为：(rear == front)。因为当 rear 指针等于 front 指针时，表示队列没有有效的元素，即队列为空。

判断环形队列满时，条件为：(rear + 1) % maxSize == front

这该怎么理解？

事实上，在含义调整后，环形队列中的 rear 变量指向的位置实际上就是预留给下次入队的数据存放的位置。

当有一个新的数据入队时，rear 指向的位置就可以存储本次入队的数据的值，然后，rear 就会加一并取余 maxSize ，用于寻找下一个可以存储入队数据的位置。

因此，当(rear + 1) % maxSize 的值刚好等于 front，那么证明该环形队列已经满了，没有地方可以存储下一次入队的值。

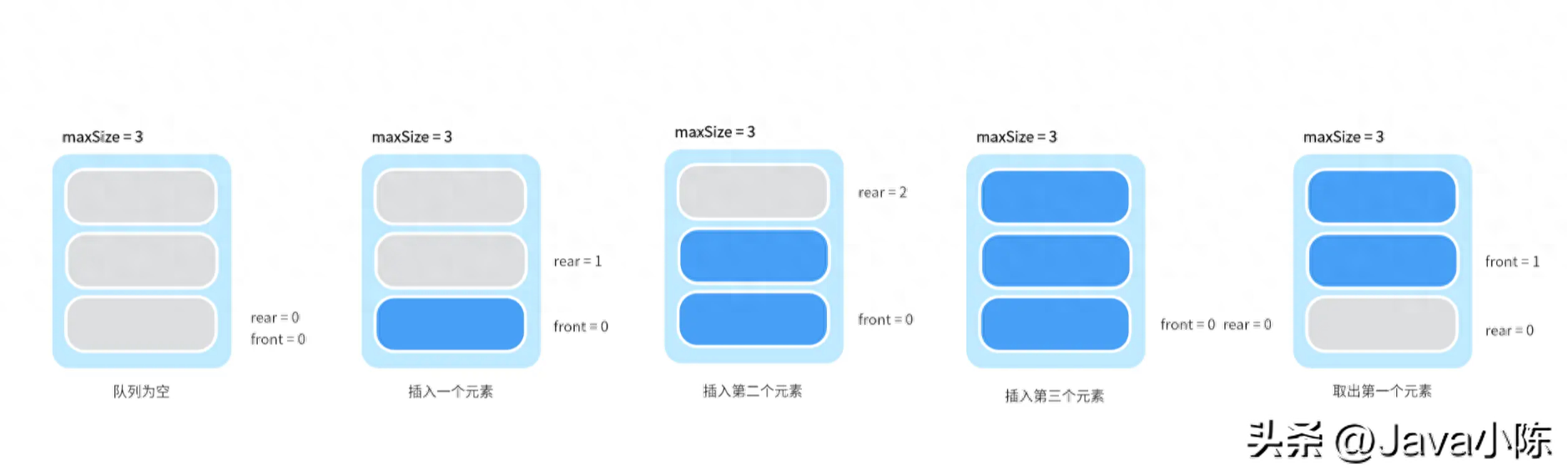
举一个例子，假设 maxSize 为 3，初始时 front 和 rear 都是0：

• 队列为空：front = 0, rear = 0
• 插入一个元素：front = 0, rear = 1
• 插入第二个元素：front = 0, rear = 2
• 插入第三个元素：front = 0, rear = 0（此时队列满，因为 (rear + 1) % maxSize 等于 front）
• 取出第一个元素：front = 1, rear = 0（此时队列有效元素个数为 2，因为 (0+3-1) % 3 == 2）

示意图如下：

优化后的队列类

优化后的代码实现如下：

class CircleArrayQueue {
    private int maxSize;
    private int front;    // 初始值为 0，指向队头数据，即首元素
    private int rear;     // 初始值为 0，指向队尾数据的下一个位置
    private int[] data;
	
    ArrayQueue(int queueMaxSize) {
        maxSize = queueMaxSize;	
        data = new int[maxSize];
    }
	
    // 判断队列是否为空
    public boolean isEmpty() {
        return rear == front;
    }
	
    // 判断队列是否满
    public boolean isFull() {
        return (rear + 1) % maxSize == front;
    }
	
    // 入队：添加数据到队尾
    public void enQueue(int num) {
        if(isFull()) {
            System.out.println("队列已满，无法入队");
            return;
        }
        data[rear] = num;
        rear = (rear + 1) % maxSize;
    }
	
    // 出队，取出队头数据
    public int deQueue() {
        if(isEmpty()) {
            throw new RuntimeException("队列为空，无法出队"); 
        }
        int value = data[front];
        front = (front + 1) % maxSize;
        return value;
    }
	
    // 显示队列的头数据（不是取出数据）
    public int headQueue() {
        if(isEmpty()) {
            throw new RuntimeException("队列为空，没有数据");
        }
        return data[front];
    }
	
    // 返回环形队列当前的元素个数
    public int size() {
        return (rear + maxSize - front) % maxSize;
    }
	
    // 打印队列
    public void showQueue() {
        if(isEmpty()) {
            System.out.println("队列为空，没有数据");
            return;
        }
        // 遍历思路，从 data[front] 遍历到 data[front + size]
        for(int i = front; i < front + size(); i++) {
            System.out.printf("data[%d] = %d\n", i%maxSize, data[i%maxSize]);
        }
    }
}

三、总结

本文详细介绍了队列数据结构的概念和应用，包括普通队列和环形队列的实现。队列是一种有序的数据结构，它在计算机科学中被广泛应用，用于管理数据和任务的顺序执行。普通队列使用数组实现，但存在内存资源浪费的问题。为了解决这个问题，我们引入了环形队列的概念，它允许队列数据的循环复用，更加高效地利用内存。