桶排序(Bucket Sort)是一种排序算法,通常用于将一组数据分割成有限数量的桶(或容器),然后对每个桶中的数据进行排序,最后将这些桶按顺序合并以得到排好序的数据集。
 图片
图片
桶排序原理
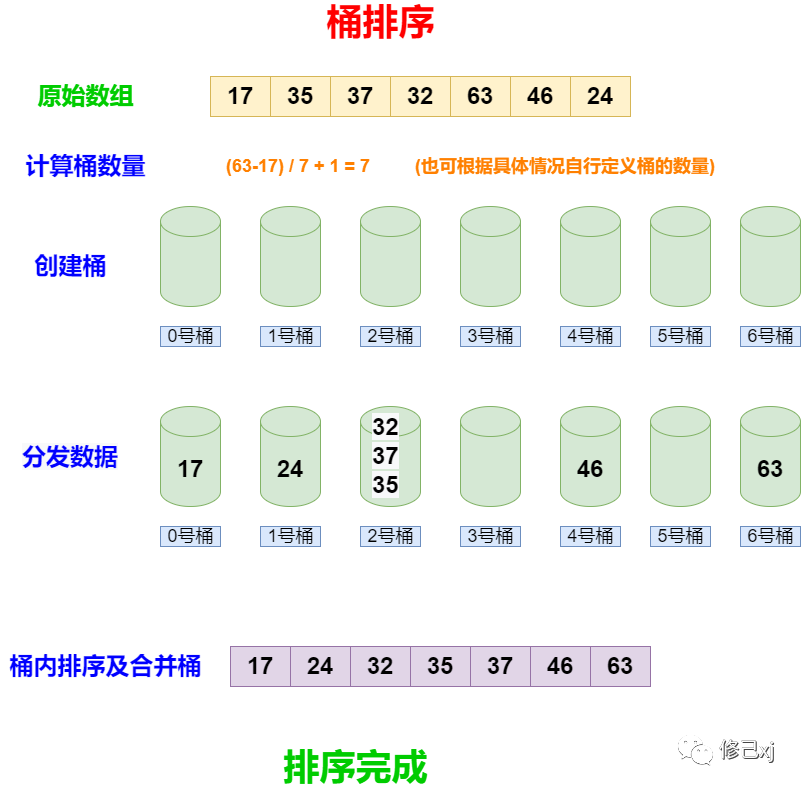
- 确定桶的数量:首先,确定要使用的桶的数量。通常,桶的数量可以根据数据范围和分布情况来确定。
- 分发数据:将待排序的元素按照一定的规则(例如,数值大小)分发到不同的桶中。
- 每个桶内排序:对每个桶内的元素进行排序。这可以使用任何排序算法,例如插入排序或快速排序。
- 合并桶:将每个桶内的元素按照桶的顺序合并,形成有序序列。
图示如下:
 图片
图片
桶排序性能分析
- 时间复杂度:桶排序的时间复杂度取决于数据的分布情况。在最理想的情况下,当数据均匀分布在各个桶中时,每个桶内的排序时间复杂度是 ,因此总体时间复杂度为 。但在最坏情况下,如果所有数据都分布在一个桶中,桶内排序的时间复杂度可以达到 。在平均情况下,桶排序通常表现为 。
- 空间复杂度:桶排序需要额外的存储空间来存储桶,因此空间复杂度为 ,其中 n 表示排序元素的个数,k 表示桶的数量。
- 稳定性:桶排序通常是稳定的,即相等元素的相对顺序在排序后不会发生变化。
使用场景
桶排序适用于以下情况:
- 数据分布相对均匀。
- 数据范围已知,可以将数据映射到有限数量的桶中。
Java 代码实现
以下是使用 Java 实现桶排序的示例代码,其中每个桶中的元素排序使用的是快速排序,快速排序的详解请参考历史博文 深入了解快速排序:原理、性能分析与 Java 实现:
public class Test {
public static void main(String[] args) {
int[] arr = new int[]{17,35,37,32,63,46,24};
System.out.println("原始数组:"+ Arrays.toString(arr));
bucketSort(arr);
System.out.println("排序后的数组:"+ Arrays.toString(arr));
}
//桶排序
public static void bucketSort(int[] arr){
int maxVal = Arrays.stream(arr).max().getAsInt();
int minVal = Arrays.stream(arr).min().getAsInt();
//计算桶的数量,+1 是保证至少有1个桶来装数据
int bucketCount = (maxVal - minVal)/arr.length + 1;
// 用于存储每个桶中元素的出现次数
int[] order = new int[bucketCount];
// 用于存储每个桶中的数据
int[][] output = new int[bucketCount][arr.length];
int len = arr.length;
//每个桶中数据的范围,+1 是至少每个桶中的数据范围为1
int rang = (maxVal - minVal)/bucketCount +1;
//将待排序的数组中的所有元素放入到桶中
for(int i = 0; i < len; i++ ){
//计算数组元素所在的桶
int index = (arr[i] - minVal) / rang ;
//将元素放入指定的桶
output[index][order[index]] = arr[i];
//添加桶元素的计数
order[index]++;
}
System.out.println("桶计数数组为:"+ Arrays.toString(order));
int k = 0;
//遍历桶,将桶中的元素放入源数组中,并对其进行快速排序
for(int i = 0; i < bucketCount; i++){
int j ;
if(order[i] > 0){
// 将桶中的元素放入源数组中
for(j = 0; j < order[i]; j++){
arr[k++] = output[i][j];
}
//对桶中的元素进行快速排序
quickSort(arr,k-j,k-1);
}
}
}
//快速排序的详解请参考历史博文 `深入了解快速排序:原理、性能分析与 Java 实现`
public static void quickSort(int[] arr,int left,int right) {
//递归结束条件left < right
if(left < right){
// 通过分区函数得到基准元素的索引
int pivotIndex = partition(arr, left, right);
//递归对基准元素左边的子数组进行快速排序
quickSort(arr,left,pivotIndex-1);
//递归对基准元素右边的子数组进行快速排序
quickSort(arr,pivotIndex+1,right);
}
}
public static int partition(int[] arr,int left,int right) {
// 选择最后一个元素作为基准元素
int pivot = arr[right];
int i = left;
//循环数组,如果满足条件,则将满足条件的元素交换到arr[i],同时i++,循环完成之后i之前的元素则全部为小于基准元素的元素
for (int j = left; j < right; j++) {
if(arr[j] < pivot){
if(j != i){
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
i++;
}
}
// 交换 arr[i] 和基准元素
int temp = arr[i];
arr[i] = arr[right];
arr[right] = temp;
//返回基准元素的下标
return i;
}
}输出结果为:
原始数组:[17, 35, 37, 32, 63, 46, 24]
桶计数数组为:[1, 1, 3, 0, 1, 0, 1]
排序后的数组:[17, 24, 32, 35, 37, 46, 63]这是一个基本的桶排序实现示例。您可以根据实际需求和数据类型进行扩展和优化。
总结
总的来说,桶排序是一种简单但有效的排序算法,特别适用于某些特定范围内数据的排序,当数据分布均匀时,性能较好。然而,对于不均匀分布的数据,其性能可能下降,因此在实际应用中需要谨慎选择。