三个主要降维技术对比介绍：PCA, LCA,SVD-51CTO.COM

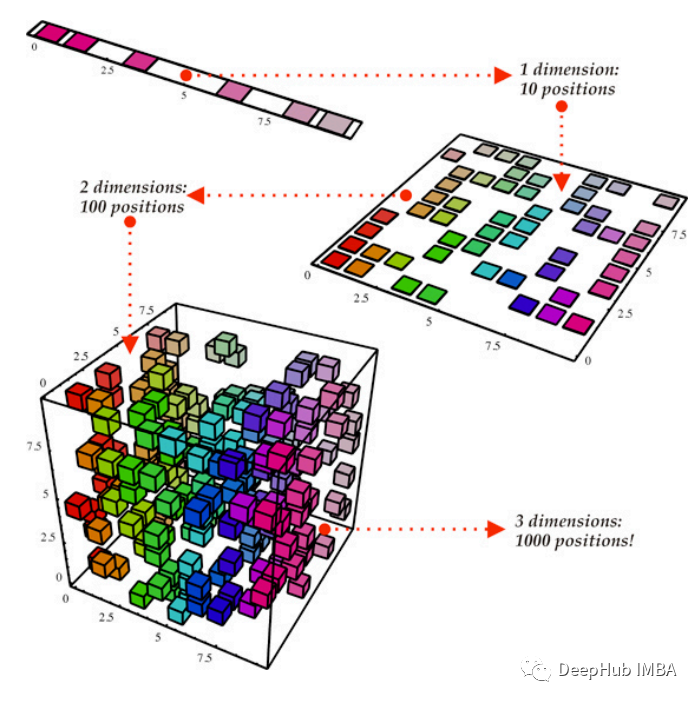
随着数据集的规模和复杂性的增长，特征或维度的数量往往变得难以处理，导致计算需求增加，潜在的过拟合和模型可解释性降低。降维技术提供了一种补救方法，它捕获数据中的基本信息，同时丢弃冗余或信息较少的特征。这个过程不仅简化了计算任务，还有助于可视化数据趋势，减轻维度诅咒的风险，并提高机器学习模型的泛化性能。降维在各个领域都有应用，从图像和语音处理到金融和生物信息学，在这些领域，从大量数据集中提取有意义的模式对于做出明智的决策和建立有效的预测模型至关重要。

本文将深入研究三种强大的降维技术——主成分分析(PCA)、线性判别分析(LDA)和奇异值分解(SVD)。我们不仅介绍这些方法的基本算法，而且提供各自的优点和缺点。

主成分分析(PCA)

主成分分析(PCA)是一种广泛应用于数据分析和机器学习的降维技术。它的主要目标是将高维数据转换为低维表示，捕获最重要的信息。

我们的目标是识别数据集中的模式，所以希望数据分布在每个维度上，并且在这些维度之间是有独立性的。方差作为可变性的度量标准，本质上量化了数据集分散的程度。用数学术语来说，它表示与平均的平均平方偏差。计算方差的公式用var(x)表示如下:

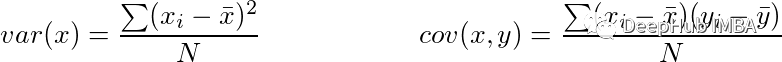
协方差量化了两组有序数据中对应元素相似的程度。用cov(x, y)表示变量x和y之间的协方差。xi表示第i维中x的值，而x柱和y柱表示它们各自的平均值。如果我们有一个维数为m*n的矩阵X，其中包含n个数据点，每个数据点有m维，那么协方差矩阵可以计算如下:

协方差矩阵包括

以尺寸方差为主要对角线元素
维度的协方差作为非对角线元素

我们的目标是确保数据广泛分散，表明其维度之间的高方差，另外一个目标是消除相关维度，这意味着维度之间的协方差应为零（表明它们的线性无关）。所以对数据进行变换的目的是使其协方差矩阵具有以下特征:

作为主要对角线元素的显著值。
零值作为非对角线元素。

所以必须对原始数据点进行变换获得类似于对角矩阵的协方差矩阵。将矩阵转换成对角矩阵的过程称为对角化，它构成了主成分分析(PCA)背后的主要动机。

PCA的工作原理

1、标准化

当特征以不同的单位度量时，对数据进行标准化。这需要减去平均值，然后除以每个特征的标准差。对具有不同尺度特征的数据进行标准化的失败可能导致误导性的成分。

2、计算协方差矩阵

如前面讨论的那样计算协方差矩阵

3、计算特征向量和特征值

确定协方差矩阵的特征向量和特征值。

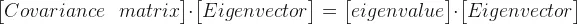
特征向量表示方向(主成分)，特征值表示这些方向上的方差大小。

4、特征值排序

对特征值按降序排序。与最高特征值相对应的特征向量是捕获数据中最大方差的主成分。

5、选择主成分

根据需要解释的方差选择前k个特征向量(主成分)。一般情况下会设定阈值，保留总方差的很大一部分，例如85%。

6、转换数据

我们可以用特征向量变换原始数据:

如果我们有m维的n个数据点X: m*n

P: k*m

Y = PX: (k*m)(m*n) = (k*n)

新变换矩阵有n个数据点，有k维。

优点

降维：PCA有效地减少了特征的数量，这对遭受维数诅咒的模型是有益的。

特征独立性：主成分是正交的(不相关的)，这意味着它们捕获独立的信息，简化了对约简特征的解释。

降噪：PCA可以通过专注于解释数据中最显著方差的成分来帮助减少噪声。

可视化:降维数据可以可视化，有助于理解底层结构和模式。

缺点

原始特征的可解释性可能在变换后的空间中丢失，因为主成分是原始特征的线性组合。

PCA假设变量之间的关系是线性的，但并非在所有情况下都是如此。

PCA对特征的尺度比较敏感，因此常常需要标准化。

异常值可以显著影响PCA的结果，因为它侧重于捕获最大方差，这可能受到极值的影响。

何时使用

高维数据：PCA在处理具有大量特征的数据集以减轻维度诅咒时特别有用。

共线的特点：当特征高度相关时，PCA可以有效地捕获共享信息并用更少的组件表示它。

可视化：它将数据投射到一个较低维度的空间，可以很容易地可视化。

线性关系：当变量之间的关系大多是线性的，主成分分析是一个合适的技术。

Python代码示例

import numpy as np
 from sklearn.decomposition import PCA
 from sklearn.preprocessing import StandardScaler
 from sklearn.model_selection import train_test_split
 from sklearn.datasets import load_iris
 
 # Load iris dataset as an example
 iris = load_iris()
 X = iris.data
 y = iris.target
 
 # Split the dataset into training and testing sets
 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
 
 # Standardize the data (important for PCA)
 scaler = StandardScaler()
 X_train_std = scaler.fit_transform(X_train)
 X_test_std = scaler.transform(X_test)
 
 # Apply PCA
 pca = PCA()
 X_train_pca = pca.fit_transform(X_train_std)
 
 # Calculate the cumulative explained variance
 cumulative_variance_ratio = np.cumsum(pca.explained_variance_ratio_)
 
 # Determine the number of components to keep for 85% variance explained
 n_components = np.argmax(cumulative_variance_ratio >= 0.85) + 1
 
 # Apply PCA with the selected number of components
 pca = PCA(n_compnotallow=n_components)
 X_train_pca = pca.fit_transform(X_train_std)
 X_test_pca = pca.transform(X_test_std)
 
 # Display the results
 print("Original Training Data Shape:", X_train.shape)
 print("Reduced Training Data Shape (PCA):", X_train_pca.shape)
 print("Number of Components Selected:", n_components)

上面代码在最初应用PCA()时没有指定组件的数量，这意味着它将保留所有组件。然后使用np.cumsum(pca.explained_variance_ratio_)计算累计解释方差。确定解释至少85%方差所需的分量数，并使用选定的分量数再次应用PCA。请注意PCA只应用于训练数据，然后在测试数据应用转换方法即可。

线性判别分析(LDA)

线性判别分析(LDA)作为一种降维和分类技术，目标是优化数据集中不同类别之间的区别。LDA在预先确定数据点类别的监督学习场景中特别流行。PCA被认为是一种“无监督”算法，它忽略了类标签，专注于寻找主成分以最大化数据集方差，而LDA则采用“监督”方法。LDA计算“线性判别器”，确定作为轴的方向，以最大限度地分离多个类。我们这里使用“Iris”数据集的示例来了解LDA是如何计算的。它包含了来自三个不同物种的150朵鸢尾花的尺寸。

Iris数据集中有三个类:

Iris-setosa (n=50)
Iris-versicolor (n=50)
Iris-virginica (n=50)

有四个特征:

sepal length in cm
sepal width in cm
petal length in cm
petal width in cm

LDA的工作步骤

1、计算三种不同花类的平均向量mi， (i=1,2,3):

Mean Vector class 1: [ 5.006 3.418 1.464 0.244]
 
 Mean Vector class 2: [ 5.936 2.77   4.26   1.326]
 
 Mean Vector class 3: [ 6.588 2.974 5.552 2.026]

每个向量包含特定类的数据集中4个特征的平均值。

2、计算类内散点矩阵(Sw)，它表示每个类内数据的分布

结果如下：

within-class Scatter Matrix:
  [[ 38.9562 13.683   24.614   5.6556]
  [ 13.683   17.035   8.12     4.9132]
  [ 24.614   8.12   27.22     6.2536]
  [ 5.6556   4.9132   6.2536   6.1756]]

3、计算类间散点矩阵(Sb)， Sb表示不同类之间的分布，公式如下:

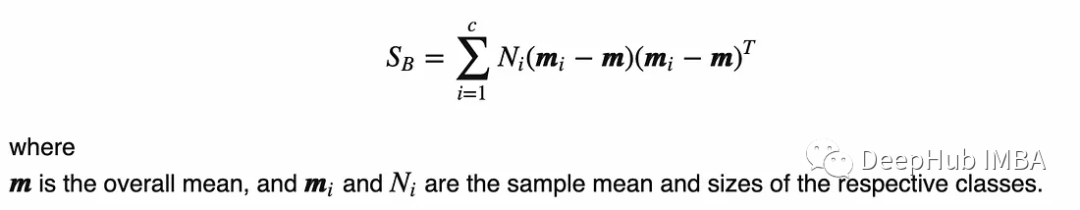
结果如下：

between-class Scatter Matrix:
  [[ 63.2121 -19.534   165.1647   71.3631]
  [ -19.534   10.9776 -56.0552 -22.4924]
  [ 165.1647 -56.0552 436.6437 186.9081]
  [ 71.3631 -22.4924 186.9081   80.6041]]

4、计算Sw-¹Sb的特征值和特征向量(类似于PCA)。在我们的例子中，有4个特征值和特征向量

Eigenvector 1:
 [[-0.2049]
  [-0.3871]
  [ 0.5465]
  [ 0.7138]]
 Eigenvalue 1: 3.23e+01
 
 Eigenvector 2:
 [[-0.009 ]
  [-0.589 ]
  [ 0.2543]
  [-0.767 ]]
 Eigenvalue 2: 2.78e-01
 
 Eigenvector 3:
 [[ 0.179 ]
  [-0.3178]
  [-0.3658]
  [ 0.6011]]
 Eigenvalue 3: -4.02e-17
 
 Eigenvector 4:
 [[ 0.179 ]
  [-0.3178]
  [-0.3658]
  [ 0.6011]]
 Eigenvalue 4: -4.02e-17

5、通过减少特征值对特征向量进行排序，并选择最上面的k。

通过减少特征值对特征对进行排序后，基于2个信息量最大的特征对构建d×k维度特征向量矩阵(称之为W)。在下面的例子中，得到了下面的矩阵:

Matrix W:
  [[-0.2049 -0.009 ]
  [-0.3871 -0.589 ]
  [ 0.5465 0.2543]
  [ 0.7138 -0.767 ]]

6、使用矩阵W (4 × 2矩阵)通过方程将样本转换到新的子空间:Y = X*W，其中X是矩阵格式的原始数据(150 × 4矩阵)，Y是转换后的数据集(150 × 2矩阵)。

优点

最大化类分离：LDA的目的是最大限度地分离不同的类，使其有效的分类任务。

降维：与PCA一样，LDA也可用于降维，其优点是考虑了类信息。

缺点

对异常值的敏感性：LDA对异常值非常敏感，异常值的存在会影响方法的性能。

正态性假设：LDA假设每个类中的特征是正态分布的，如果违反了这个假设，它可能无法很好地执行。

需要足够的数据：LDA在每个类只有少量样本的情况下可能表现不佳。拥有更多的样本可以改善类参数的估计。

何时使用

分类任务：当目标是将数据分类到预定义的类中时，LDA是有益的。

保存类信息：当目标是在降低维数的同时保留与区分类相关的信息时，LDA非常有用

正态性假设成立：当类别内的正态分布假设成立时，LDA表现良好。

监督降维：当任务需要在类标签的指导下进行降维时，LDA是一个合适的选择。

Python代码示例

import numpy as np
 import pandas as pd
 from sklearn.model_selection import train_test_split
 from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
 from sklearn.datasets import make_classification
 from sklearn.preprocessing import StandardScaler
 
 # Generate a sample dataset
 X, y = make_classification(n_samples=1000, n_features=20, n_classes=2, random_state=42)
 
 # Split the data into training and test sets
 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
 
 # Standardize the features (important for LDA)
 scaler = StandardScaler()
 X_train = scaler.fit_transform(X_train)
 X_test = scaler.transform(X_test)
 
 # Initialize LDA and fit on the training data
 lda = LinearDiscriminantAnalysis()
 X_train_lda = lda.fit_transform(X_train, y_train)
 
 # Calculate explained variance ratio for each component
 explained_variance_ratio = lda.explained_variance_ratio_
 
 # Calculate the cumulative explained variance
 cumulative_explained_variance = np.cumsum(explained_variance_ratio)
 
 # Find the number of components that explain at least 75% of the variance
 n_components = np.argmax(cumulative_explained_variance >= 0.75) + 1
 
 # Transform both the training and test data to the selected number of components
 X_train_lda_selected = lda.transform(X_train)[:, :n_components]
 X_test_lda_selected = lda.transform(X_test)[:, :n_components]
 
 # Print the number of components selected
 print(f"Number of components selected: {n_components}")

奇异值分解(SVD)

奇异值分解是一种矩阵分解技术，广泛应用于线性代数、信号处理和机器学习等领域。它将一个矩阵分解成另外三个矩阵，原始矩阵以简化形式表示。

SVD的工作步骤

1、矩阵分解

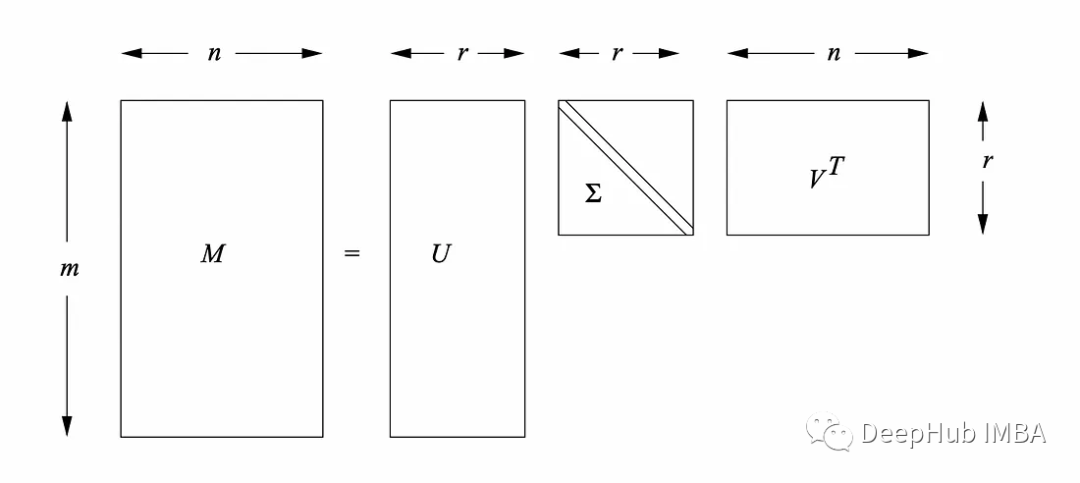
给定大小为M × n的矩阵M(或有M行n列的数据)，奇异值分解将其分解为三个矩阵:M = u *Σ * v *

其中U是一个m × m正交矩阵，Σ是一个m × r对角矩阵，V是一个r × n正交矩阵。r是矩阵M的秩。

Σ的对角线元素为原矩阵M的奇异值，按降序排列。U的列是m的左奇异向量，这些向量构成了m的列空间的正交基，V的列是m的右奇异向量，这些向量构成了m的行空间的正交基。

2、简化形式(Truncated SVD)

对于降维，通常使用截断版本的奇异值分解。选择Σ中前k个最大的奇异值。这些列可以从Σ中选择，行可以从V * *中选择。由原矩阵M重构出一个新的矩阵B，公式如下:

B = u * Σ，B = V * A

其中Σ只包含原始Σ中奇异值的前k列，V包含原始V中奇异值对应的前k行。

优点

降维：SVD允许通过只保留最重要的奇异值和向量来降低维数。

数据压缩：SVD用于数据压缩任务，减少了矩阵的存储需求。

降噪：通过只使用最显著的奇异值，奇异值分解可以帮助减少数据中噪声的影响。

数值稳定性：奇异值分解在数值上是稳定的，适合于求解病态系统中的线性方程。

正交性：SVD分解中的矩阵U和V是正交的，保留了原矩阵的行与列之间的关系。

推荐系统中的应用：奇异值分解广泛应用于推荐系统的协同过滤。

缺点

计算复杂度：计算大型矩阵的完整SVD在计算上是非常昂贵的。

内存需求：存储完整的矩阵U、Σ和V可能会占用大量内存，特别是对于大型矩阵。

对缺失值的敏感性：SVD对数据中的缺失值很敏感，处理缺失值需要专门的技术。

何时使用

降维：当目标是在保留数据基本结构的同时降低数据的维数时。

推荐系统：在基于协同过滤的推荐系统中，SVD用于识别捕获用户-物品交互的潜在因素。

数据压缩：在需要压缩或近似大型数据集的场景中。

信号处理：在信号处理中，采用奇异值分解进行降噪和特征提取。

主题建模：SVD被用于主题建模技术，如潜在语义分析(LSA)。

Python代码示例

import numpy as np
 from sklearn.model_selection import train_test_split
 from sklearn.decomposition import TruncatedSVD
 from sklearn.datasets import make_classification
 from sklearn.preprocessing import StandardScaler
 
 # Generate a sample dataset
 X, y = make_classification(n_samples=1000, n_features=20, n_classes=2, random_state=42)
 
 # Split the data into training and test sets
 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
 
 # Standardize the features (important for SVD)
 scaler = StandardScaler()
 X_train = scaler.fit_transform(X_train)
 X_test = scaler.transform(X_test)
 
 # Initialize SVD and fit on the training data
 svd = TruncatedSVD(n_compnotallow=X_train.shape[1] - 1) # Use one less component than the feature count
 X_train_svd = svd.fit_transform(X_train)
 
 # Calculate explained variance ratio for each component
 explained_variance_ratio = svd.explained_variance_ratio_
 
 # Calculate the cumulative explained variance
 cumulative_explained_variance = np.cumsum(explained_variance_ratio)
 
 # Find the number of components that explain at least 75% of the variance
 n_components = np.argmax(cumulative_explained_variance >= 0.75) + 1
 
 # Transform both the training and test data to the selected number of components
 X_train_svd_selected = svd.transform(X_train)[:, :n_components]
 X_test_svd_selected = svd.transform(X_test)[:, :n_components]
 
 # Print the number of components selected
 print(f"Number of components selected: {n_components}")

总结

在主成分分析(PCA)、线性判别分析(LDA)和奇异值分解(SVD)之间的选择取决于数据的具体目标和特征。以下是关于何时使用每种技术的一般指导原则:

主成分分析：

当目标是降低数据集的维数时。
在捕获数据中的全局模式和关系至关重要的场景中。
用于探索性数据分析和可视化。

线性判别分析：

在分类问题中，增强类之间的分离。
当有一个标记的数据集时，目标是找到一个最大化阶级歧视的投影。
当正态分布类和等协方差矩阵的假设成立时，LDA特别有效。

奇异值分解：

当处理稀疏数据或缺失值时。
推荐系统的协同过滤。
奇异值分解也适用于数据压缩和去噪。

三个技术的对比：

无监督vs有监督学习：PCA是无监督的，而LDA是有监督的。根据标记数据的可用性进行选择。

类可分离性：如果目标是改进类可分离性，那么首选LDA。PCA和SVD关注的是总体方差。

数据特征：数据的特征，如线性、类别分布和异常值的存在，会影响选择。

特定于应用程序的需求：考虑应用程序的特定需求，例如可解释性、计算效率或对丢失数据的处理。

综上所述，PCA适用于无监督降维，LDA适用于关注类可分性的监督问题，而SVD具有通用性，可用于包括协同过滤和矩阵分解在内的各种应用。