在这里核心就是算法思想叫做"三路切分"。 “三路切分” 曾是 EMC 面试中的常客,这个名词听起来很高大上,但是简单来说就是将数组切分成三部分。 我再回忆一下“快速排序”算法。
// 交换数组中两个元素的值
function swap(a, i, j) {
const temp = a[i];
a[i] = a[j];
a[j] = temp;
}
function qsort(a, b, e) {
// 边界处理
if (b >= e || b + 1 >= e) {
return;
}
// 第一步:划分子结构
const mid = b + ((e - b) >> 1);
// 第二步:找到根节点,获取信息
const x = a[mid];
let l = b;
let i = b;
let r = e - 1;
while(i <= r) {
if (a[i] < x) {
swap(a, l++, i++);
} else if (a[i] === x) {
i++;
} else {
swap(a, r--, i);
}
}
// 第三步:将根节点信息传递给左右子数组
qsort(a, b, l);
qsort(a, i, e);
}
// 主函数,将数组nums排序
function quickSort(nums) {
if (nums == null)
return;
qsort(nums, 0, nums.length);
return nums;
}那为什么需要“三路切分”,它的意义是什么?这里看一个例子:
输入:[2, 1, 0]
输出:[0, 1, 2]
如何只通过 swap 操作,将这个数组进行排序?
要求:你的时间复杂度需要是 O(N),空间复杂度需要是 O(1)。在快速排序的时候,我们通过一个整数 x 将数组切分成小于、等于、大于三部分。问题的关键就是如何在时间复杂度 O(N),空间复杂度 O(1) 条件下完成这个操作。
对于快速排序而言,通过一个整数 x 将数组切分成:
- 小于 x 部分;
- 等于 x 的部分;
- 大于 x 的部分;
本质上来说,其实包含四部分:
- 小于 x 部分;
- 等于 x 的部分;
- 还未处理数的部分;
- 大于 x 的部分;
 图片
图片
我们假设这四部分分别对于四个区间:
- 小于 x 部分:[0, l);
- 等于 x 的部分[l, i);
- 还未处理数的部分[i, r];
- 大于 x 的部分(r, length);
 图片
图片
在进行排序是,我们划分结构读取的是 [i, r) 区间的值。 在 [i, r) 区间中的值 x 取值只可能是下面 3 种情况:
- x 属于 [0, l) 区间;
- x 属于 [l, i) 区间;
- x 属于 (r, length) 区间;
快速排序的目的就是将[i, r]区间的取,全部插入到其他区间,完成排序操作。
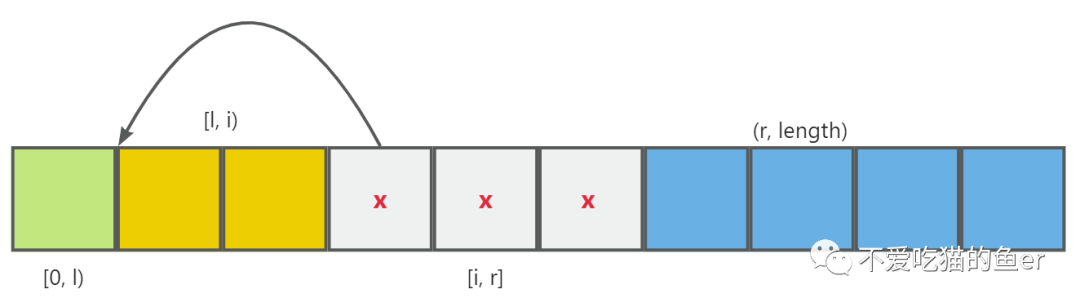
1. x 属于 [0, l) 区间
如果 x 属于 [0, l) 区间,那么我们就需要将 x 插到 [0, l) 区间。
 图片
图片
将 x 插入到 [0, l) 这个区间除了像插入排序一样一个一个地移动,还有没有更好的办法呢?
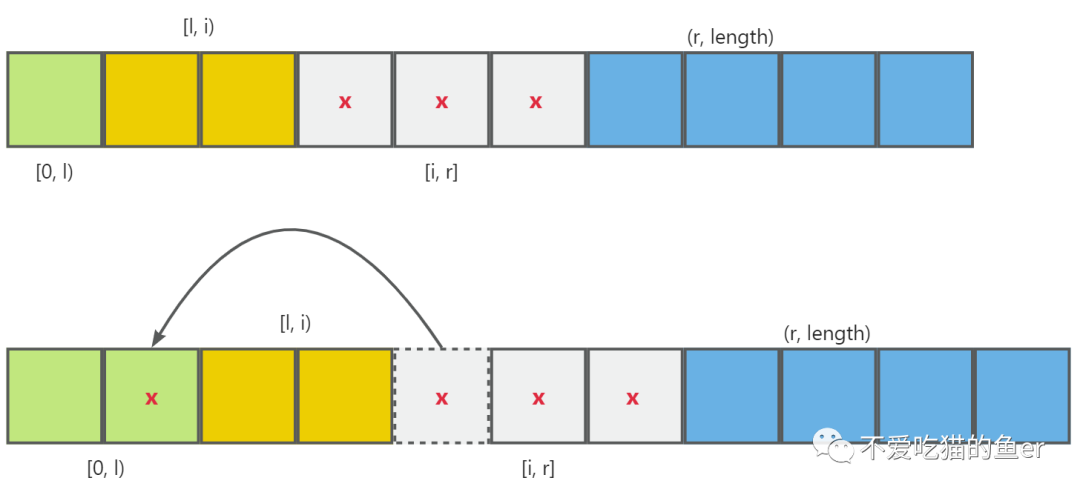
答案是,有,我并不需要一个一个移动!因为 [l, i) 区间里面全都是等于 x 的部分,只需要将的 nums[l] 与 nums[i] 进行交换即可。这就回答了第一个问题?为什么我们在节点排序处理是通过 swap 操作?
 图片
图片
这时候整个[l, i) 区间整体向右平移一步,整个[i, r) 区间也整体向右平移一步。所以需要执行 l++, i++。
if (a[i] < x) {
swap(a, l++, i++);
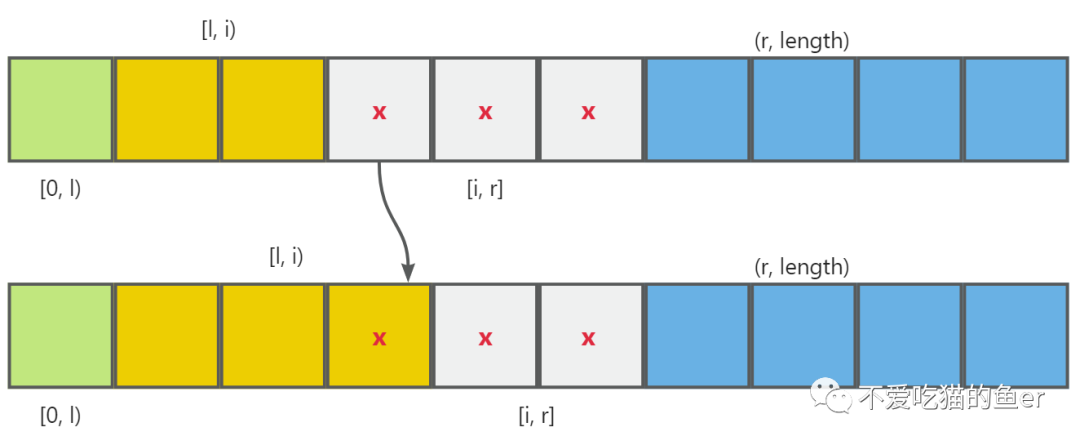
}2. 如果 x 属于 [l, i) 区间
如果 x 属于 [l, i) 区间,也就是等于 x 的部分,那么我们就需要将 x 插到 [l, i) 区间,这里就比较简单了,只需要为 [l, i) 区间扩展一下就好了。相当于在 [l, i) 区间添加了一个元素,所以需要执行 i++。
 图片
图片
else if (a[i] === x) {
i++;
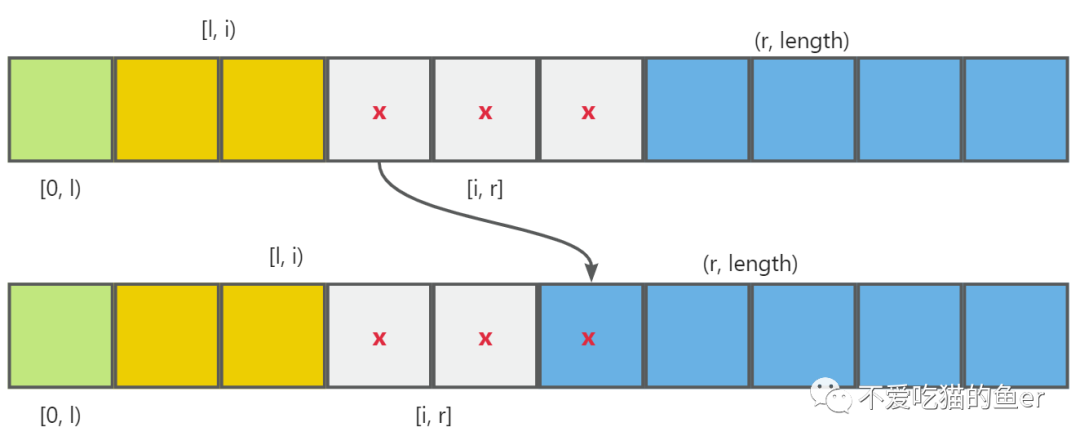
}3. 如果 x 属于 (r, length) 区间
如果 x 属于 (r, length) 区间,也就是大于 x 的部分,那么我们就需要将 x 插到 (r, length) 区间,相当于 (r, length)区间向左平移了一步,这时候 r--。
 图片
图片
else {
swap(a, r--, i);
}最终状态:所有的数都被处理之后,[i, r] 区间肯定为空集。由于两边都是取闭,那么必然当 i > r 的时候,[i, r] 才是空集。原本的四个区间,变成三个区间。
- [0, l) 小于 x 的区间
- [l, i) 等于 x 的区间
- [i, length) 大于 x 的区间。
注意此时由于 i > r,实际上 i = r + 1,那么区间 (r, length) 就是 [i, length)。 由于最终状态是将一个乱序的数组切分成三部分,所以这个方法又叫三路切分。
接下来我们看一个例子:
列1:只出现一次的数字
给你一个 非空 整数数组 nums ,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。 你必须设计并实现线性时间复杂度的算法来解决此问题,且该算法只使用常量额外空间。
示例 1 :
输入:nums = [2,2,1]
输出:1
示例 2 :
输入:nums = [4,1,2,1,2]
输出:4
示例 3 :
输入:nums = [1]
输出:1这道题目想想用“三路切分”如何实现?
任意选中一个数字 x ,将数组分成三份,那么是不是会出现三种情况?
- 第一种:只出现一次的数字在 x 左边,那么左边区域的长度为奇数,因为其他的数都是出现了两次。
- 第二种:选中的 x 就是只出现一次的数组,左右两边区间长度都为偶数。
- 第三种:只出现一次的数在右边,那么右区间的长度为奇数。
通过分析可知 3 种情况中,只有第二种情况得到了结果。而第一种情况只出现 1 次的数在左区间时,只需要递归地处理左区间;第三种情况只出现 1 次的数在右区间时,只需要递归地处理右区间。
function swap(A, i, j) {
const t = A[i];
A[i] = A[j];
A[j] = t;
}
function threeSplit(a, b, e) {
// 边界情况
if (b >= e) {
return 0;
}
/*********************核心代码****************************/
// 第一步:划分子结构
const mid = b + ((e - b) >> 1);
// 第二步:获取根节点信息 x
const x = a[mid];
// 根据 x 将数组一分为三 【三路切分】
let l = b;
let i = b;
let r = e - 1;
while(i <= r) {
if (a[i] < x) {
// 小于 x 的部分
swap(a, l++, i++);
} else if (a[i] === x) {
// 等于 x 的部分
i++;
} else {
// 大于 x 的部分
swap(a, r--, i);
}
}
// 第三步:将根节点的信息传递左右子子树
// 切分完毕之后,只有三个区间
// [b, l) [l, i) [i, N)
// 中间区间
if ((i - l) === 1) {
return a[l]
}
// 左区间
if (((l - b) % 2) == 1) {
return threeSplit(a, b, l);
}
// 右区间
return threeSplit(a, i, e);
/*********************核心代码****************************/
}
// 主函数
function main(nums) {
if (nums == null || nums.length <= 0) {
return 0;
}
return threeSplit(nums, 0, nums.length);
}总结
尽管与位运算相比,这种解法算不上最优,不过也不失一种有趣的解法。数组其实是另外一种形式的二叉树,只不过有时候需要我们动态地把左/右子树给切分出来,不同的切分方式,可以解决不同的问题。



































