一、数据是什么样子的？
1、正态分布
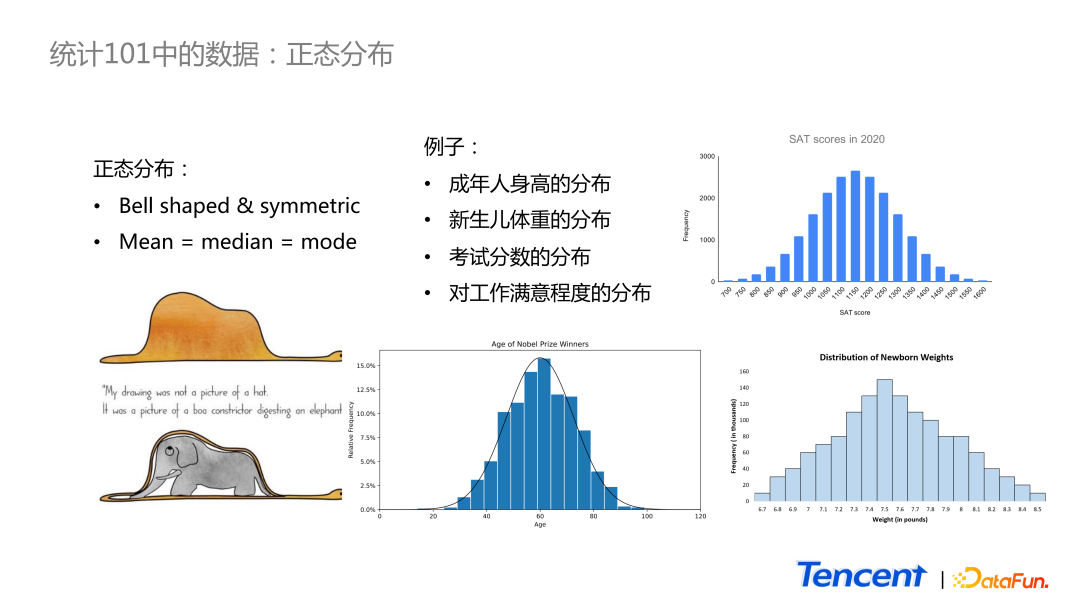
统计学教材中首个连续分布就是正态分布。如图中所示，正态分布看上去是一个对称的钟型分布图形。在正态分布里，均值、中位数和众数一般是相等的。教材中有两个经典的正态分布的例子：考试分数的分布和新生儿体重的分布。还比如诺贝尔奖得主年龄的分布，也是正态分布。
虽然正态分布很经典，应用很广泛，但是从个人角度而言，这个分布在日常生活中感知并不强烈。用成年人的身高来举例，虽然我们知道身边很多朋友的身高，但是在脑海里很难形成一个很鲜明的分布的概念。
而在日常生活中，让我感知比较强烈的是另外一个分布——Power Law。
2、The Power Law
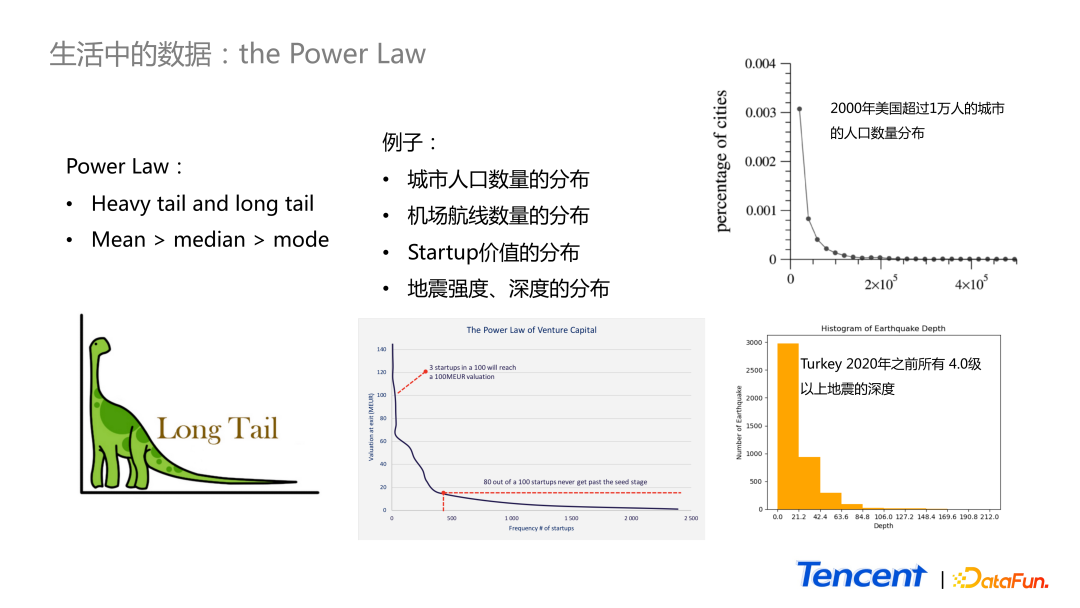
Power Law 分布如图中雷龙的样子，在较小的范围里相对小的值有很高的概率出现，而右边的尾巴很长，极大值可以很大，但出现的频率却很低。在这样的分布里，因为存在极大值，所以其均值大于中位数大于众数。举一些例子：
- 常见的城市人口数量分布，2000 年美国超过 1 万人的城市的人口数量分布，是一个很明显的 Power Law 分布，大城市的数量极少。
- 在自然界中，地震深度的分布也属于 Power Law 分布，比如上图所示的 2020 年之前土耳其所有 4.0 级以上地震的深度的分布。
- Startup 价值的分布，那些 venture capital 真正想投资追逐的是最后的尾部，但凡能命中 top one，不会在意 top two。
为什么人们对 Power Law 的分布感知更强烈呢？比如提到城市人口数量，大家能马上想到的大城市只有少数几个，超过 2000 万人的城市如北京、上海，小一些的 400 万人口的城市如大连等。剩下一些非常小的城市，甚至想不起来名字，也不会在脑海里浮现出来。又比如每天上下班通勤中，大多数路口的车流量实际上并不高，只有个别路口非常堵。说起来哪最堵，大家心里都比较清楚。因此在日常生活中对 Power Law 感知更加强烈。
3、为什么 Power Law 常见？
为什么 Power Law 数据在日常生活中这么常见？
从抽象的角度来讲，human-related networks 数据最终都会呈现出 Power Law 的情况。因为人类的喜好是有共性的，做出的选择大多都是相似的，这导致了个别数据非常集中。
比如，我们可以把每个人想象成一个点，若在 Facebook 或者 Twitter 上有 follow 好友的关系，就将这两点连线，最终呈现出如上图 1 的关系。从内容生态角度而言，也可以把内容或创作者看作一个点，若同一个 c 端用户消费内容就画一条边，最终呈现的也是如上图 1 的样子。所以这种有 pattern 的图，每一个节点的边的数量大概率呈现为 Power Law。而真正随机产生的一个 network graph 则是像上图 2。
这就是抽象机制。
理论机制也存在多种，这里举 3 个例子：
Proportional random growth 机制
假设有固定数量的随机变量，用 s 表示，每一个时间可取到的值=上一个时间的值 × 随机变量 γ。这里面的 γ 是 iid 的随机变量，有 pdf f，γ>0。在 t+1 时刻，随机变量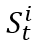
大于某一个固定值的概率，我们把它定义为 function 
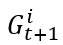。它与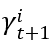 
相关，所以如图中间公式所示。最终可以写成一个期望的形式，这个期望又可以展开成一个积分形式，因为已知 density function 是 f，如果满足一定条件，system 最终会达到一个均衡状态。均衡状态是指 function G 不随时间的变化而变化，就可把时间的角标去掉， 得出 function G 等于积分里面的 function G 等式。
function G 的 solution 可以是什么形式？如果 function a over x to the power k 满足积分等于 1 的条件下，function G 的 parameter k，能满足积分形式的 G 就是最后等式的一个 solution。它恰好是一个 Power Law 分布的 1 减 CDF 的 function。所以在 proportional random growth 这种情况下，当系统达到均衡的状态，会得到一个 Power Law 的分布。
Transformations of PLs
当我们对 Power Law 的 random variable 进行一些操作，比如把它们相加、相乘、取最小值或取最大值等。最终都会得到一个新的 Power Law 分布。
Matching and equilibriumn
第三个形成机制是经济学的一个理论，叫做 matching。分享一个 CEO 工资的例子。
大家都知道 CEO 的工资都很高，而且大公司往往比小公司高了很多。这是为什么呢？
先来介绍背景，公式中的 n 代表公司的角标，S of n 表示第 n 个公司的规模；m 表示 CEO 候选人角标，T（m）表示 CEO 才华价值；ω(m) 表示第 m 个 CEO 候选人的薪水范围。
针对每一个公司，都希望能最大化 T(m)-ω(m) 的差值。这里面还有一个参数 γ，表示大公司相对于小公司而言，在短时间内更难被 CEO 改变，即 γ＜1。
若存在最优解，那么 objective function 的一阶导数是 0，变量是 m，因此若对 t 取导，乘以它减去 γ 的导数，最终等于 0，于是得出一个表达形式。
在 paper 里面，基于历史数据，researcher 对 s 的形式作了假设，假设公司规模服从帕累托分布，有参数 γ 对于 CEO 候选人的才华价值的导数，并且右侧尾巴是满足一定指数的。经过一番处理之后，最终得出上图中的公式。
这篇 paper 里面，他们研究对象是世界 500 强的公司，按公司规模从大到小排序， n star 250 就是第 250 个公司。最后 paper 里做了一些 calibration，发现 γ 的值基本上就是 1，β 与 α 的比值约为 2: 3 。
还有一个有趣的结论，他们发现在最大的和中位数的公司中，两者的 CEO 的才华价值差异小于 1% ，但是前者的工资却是后者的 5 倍。这也解释了为什么 CEO 的工资的分布属于 Power Law。
另外也从侧面印证了，在许多优化问题里，若原始的数据存在 Power Law 分布，它最后的结果很可能也是 Power Law 的分布。
4、内容生态数据：the Power Law
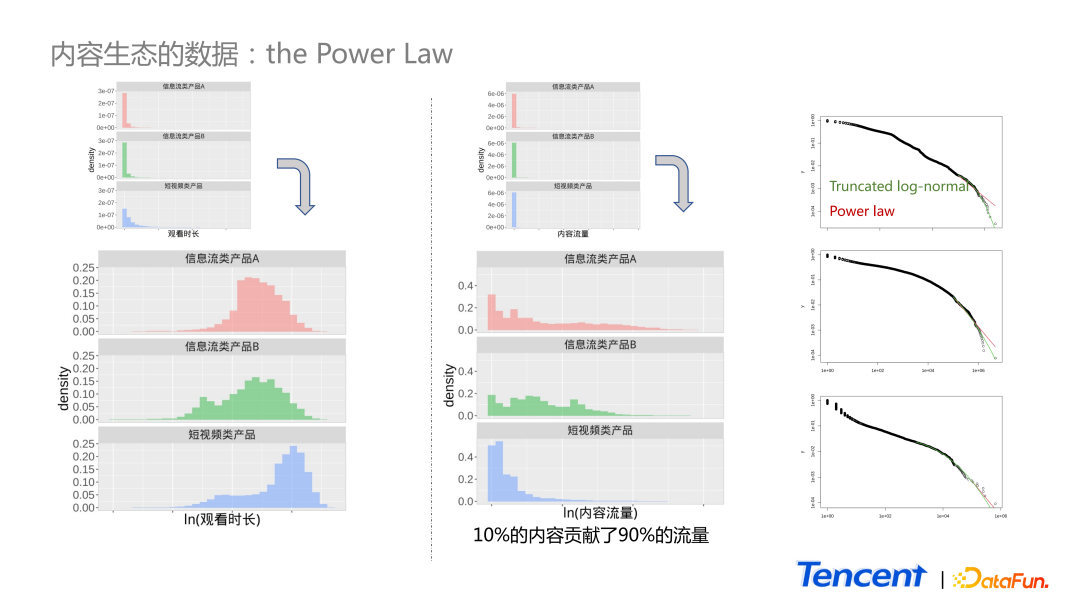
如图中所示，展示了 3 个产品 c 端用户单天消费时长的分布。这里选了 3 个产品，蓝色的图为短视频产品，红色和绿色为信息流类的产品。
上面小图是原始数据的分布，由于第一个柱子特别高，无法查看具体的 pattern，因此取了对数进行分析，取对后发现均类似钟型的对称分布。
中间的图与左侧图类似，中间图为内容流量的分布，依旧看不出什么 pattern。取对后发现，它依旧是 Power Law 形式的分布，右侧有一个长尾巴，大部集中在前面比较小的范围里。所以对比单天的用户消费时长和内容流量的分布，是类似的，其实在我们的生态里面，10% 的内容贡献了 90% 的流量。
大多数时候，大家遇到右侧尾部很长的分布，会对尾部更感兴趣。比如对这三个数据，分别用 truncated，log normal 还有 Power Law 对它们做拟合。但并未发现 Power Law 或 log normal 的显著优势。
二、我们可以做什么？
1、厚尾分布及其性质
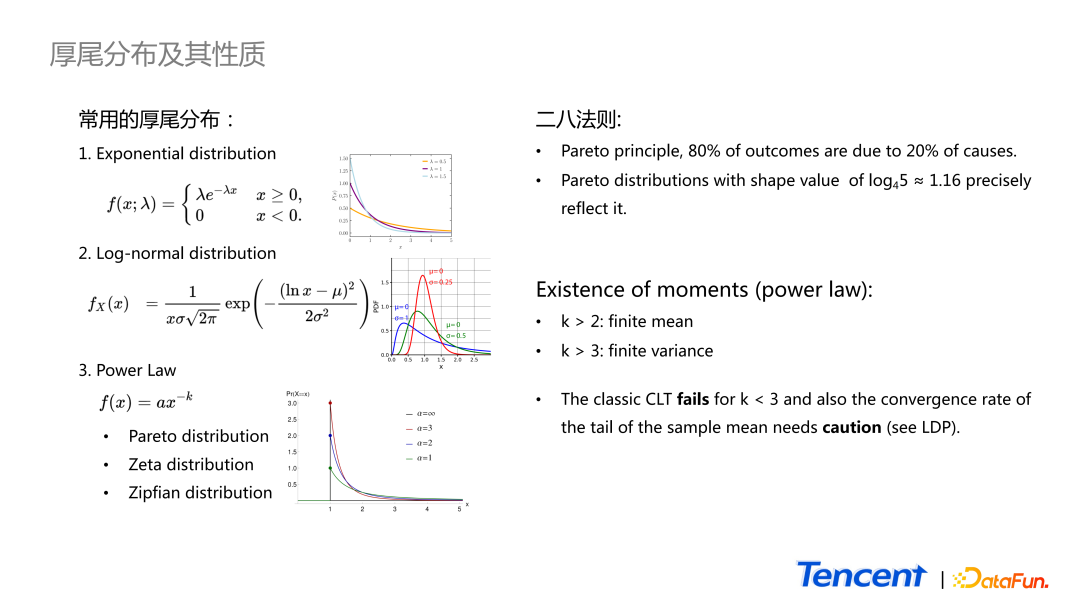
当我们看到 Power Law 的数据，可以做些什么呢？
先来看 Power Law 分布具体的定义和性质。基本上看到与雷龙相似的分布就认为是Power Law。但这只是一个比较通用的概念。准确来说，我们只能说它是一个厚尾分布。厚尾分布根据尾巴的厚度从薄到厚，常用的有以下三种：
- 第一种是大家熟悉的指数分布。
- 尾巴稍微厚一点的就是 Log-normal 分布，就是随机变量 take log 之后是正态的，所以它就是一个 log-normal distribution。常用的是 truncate 以后的 version，比如我们更关心它右侧长的是什么样子的。
- 最后一个指的是一类分布，最著名的例子就是帕累托分布，还有 Zeta 分布、Zipfian 分布。
Power Law 分布有如下性质：
其中最著名的就是二八法则，又称为 Pareto principle。表示 80% 的结果均由 20% 的原因造成的。更准确地讲，它是一个特殊的帕累托分布，所产生的现象就是 ship parameter 等于 1.16 的帕累托分布。在日常工作中，我们可以花更多的精力和资源去抓住重要的 20%，这样就能拿到大部分的收益。
第二个性质是针对整个 Power Law 的，当参数 k 大于 2，它才有 finite mean；当参数 k 大于 3，它才有 finite variance。这就存在一些潜在问题，如应用很广的理论 central limit theorem，它要求随机变量的均值和方差都是定义良好的。但若 Power Law 存在，且 variance 不在有限的情况下，会导致 central limit theorem 失效；或者是 variance 很大的时候，其收敛速度会很慢。另外一个问题是，central limit theorem 只描述了 sample mean 中心部分分布的样子，它会最终收敛成正态分布，但并不关注尾部特征。对这部分感兴趣的同学可以看一下大偏差理论 large deviation principle。
Power Law 的这两个性质，可能会在日常应用中带来一些风险。比如在 AB 实验中，可能因为个别极端值的存在，导致 AB 分组本身存在一定的差异。
第二个问题是 10-Sigma event 会比我们预想中更容易发生。有一个经典的例子，在 1998 年时，名为 long term capital management 的对冲基金因为假设了某个货币的一些 movements 是服从正态分布的，从而低估了风险，结果发生了 10-Sigma event 的发生，这是一个小概率的事情，但导致了他们破产。
2、Power Law 应用例子
（1）网页搜索浏览
第一个例子，谷歌的网页浏览量基本上是服从 Zipf’s law。谷歌在做网页索引时，最高优的索引池的量级是相对较小的，只有百万级别，网页的索引可以达到秒级的更新。而谷歌的全量索引池是千亿级别的，只能达到小时或者天级的更新。即便是这样，只有一个规模如此之小的高优索引池，也可让谷歌的搜索提供高质量的搜索体验，就是因为 Zipf’s law 的存在。
另外一个原因是，部分网页不需要更新这么快，比如 Wikipedia 中线性规划的网页，质量很高，但更新频率很慢，而且不会存在颠覆性的更新，所以即便它是一个好的网页，也不需要进最高优的索引池。一般只有新闻或者是体育赛事的实况信息才需进入高优搜索池。
第二个例子也与搜索相关，现在很多搜索结果都是在右上方 knowledge panel，只有一小部分会被高频率地访问到。因此只有这些 hot part 才会被频繁地更新，而那些 cold part 更新速度比较慢。
我们可以将这两个优点利用得很好，但需要注意 Power Law 带来的问题。
比如大家以 URL 为单位，以点击量作为观测数据进行 AA 实验，即便是百万量级，最后也可能因为一两个网页导致均值上显著的差异。因此在谷歌绝大部分实验都是以 query 为单位进行的。为了克服这个问题还有其他方法，拿到实验数据时并不能直接得出结论，而是需要进一步做一些分析，常用分析方法有 DID、propensity score matching 或者是 propensity score weighting 等。
（2）书店对比
第二个例子是两个书店的对比。
Barnes & noble 是美国常见的连锁实体书店。Amazon 是电商。Barnes & noble 的藏书量仅几十万本，但是亚马逊只有 30% 销售的是 Barnes & noble 没有的书。正因为二八法则的存在，这样小的实体书店才得以存活下来，并且规模是越来越大。这就类似阿基米德说的，给一个杠杆，就能敲起地球。
三、我们是怎么做的？
1、内容中台：全链路统筹优化，以小换大
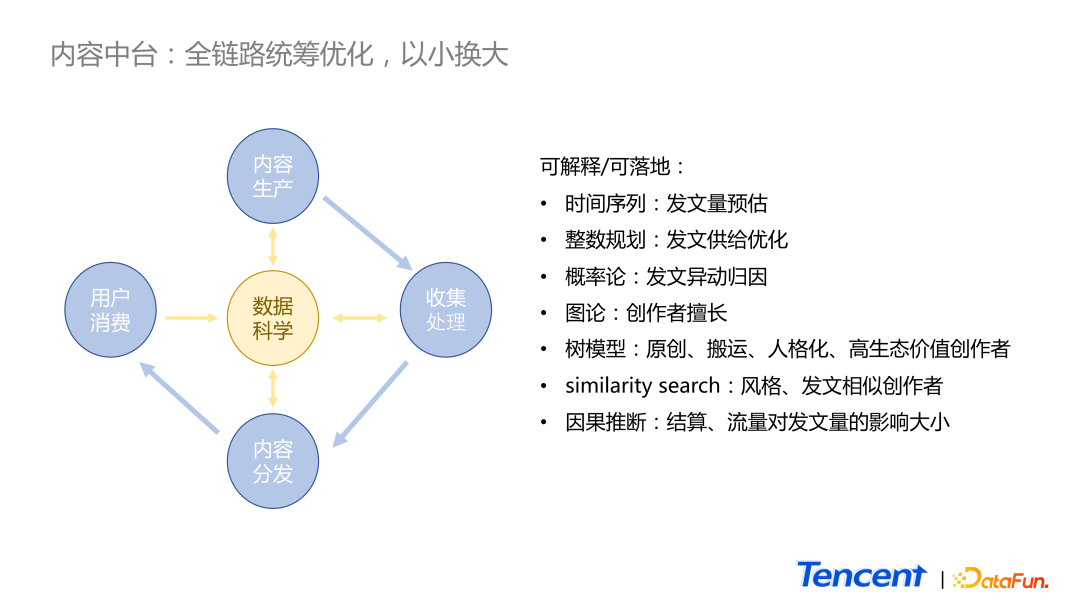
如图所示，在传统的内容生态行业里，供应链流程如下：
- 首先需要内容创作者进行内容生产。
- 然后业务将数据收集并进行进一步的加工，如安全性、分类、打 tag 等。
- 接着进入推荐或者搜索的场景进行分发。
- 最终才能触达到 c 端的用户。
在传统的供应链里，每一个环节只能接触到上游或者下游的数据，很难做到全链路的统筹优化。而在数据科学中心则会得到全业务链路每一个环节的数据，因此我们可以做的优化工作有很多。举 3 个偏传统统计和概率的例子：
- 内容生产环节上，可以通过时间序列进行发文预估，甚至可进一步地让业务对各自的进行预算预估和分配资源。
- 通过整数规划找到一些相对不重要的内容或创作者，调整策略。
- 概率论的应用，实现自动对发文量的异动进行归因，节省了人力的成本。
在信息内容的收集和处理环节也有很多比较偏算法的项目：
- 用图论描述创作者是什么样子的。比如一个创作者他擅长的话题和程度，或者表示原创、搬运或人格化程度很高等。
- 通过树模型，对创作者进行发文和创作的风格或相似性进行对比。
- 通过因果推断找到对创作者产生影响的抓手。
2、策略优化
我们常用流量补贴政策、流量补贴策略和结算补贴策略激励创作者，因此希望知道这些策略对创作者的影响大小。以下分享 3 个日常工作中的案例。
（1）整数规划
这是一个发文策略中整数规划的例子。
这个项目是为了找到高生态价值的头部作者，从而进行补贴策略的调整。r 表示业务的收益函数，c 表示成本函数。在绝大多数情况下，收益函数都是 concave 的函数，成本函数都是一个 convex 的形式，所以 objective function 形式比较好。最后是一个 concave，很适合做 maximization。
这里有一些 constraints。我们不希望业务对创作者产生过大的影响，因此对于每一个业务和赛道，需要有一个限制。这里面的 x1 到 xn 表示有 n 个创作者，如果等于 1，需要进入到新策略里，若等于 0 就不放到新策略里。通常来讲 function r 和 function c 形式是多变的，但我们可以用 piecewise linear function 进行预估。图中可看出最终这个问题就会转化成一个形式非常好的混合的整数规划，可以用 branch and cut 方法进行求解，能保证理论上有唯一的最优解。
（2）创作者擅长领域定义 & 挖掘
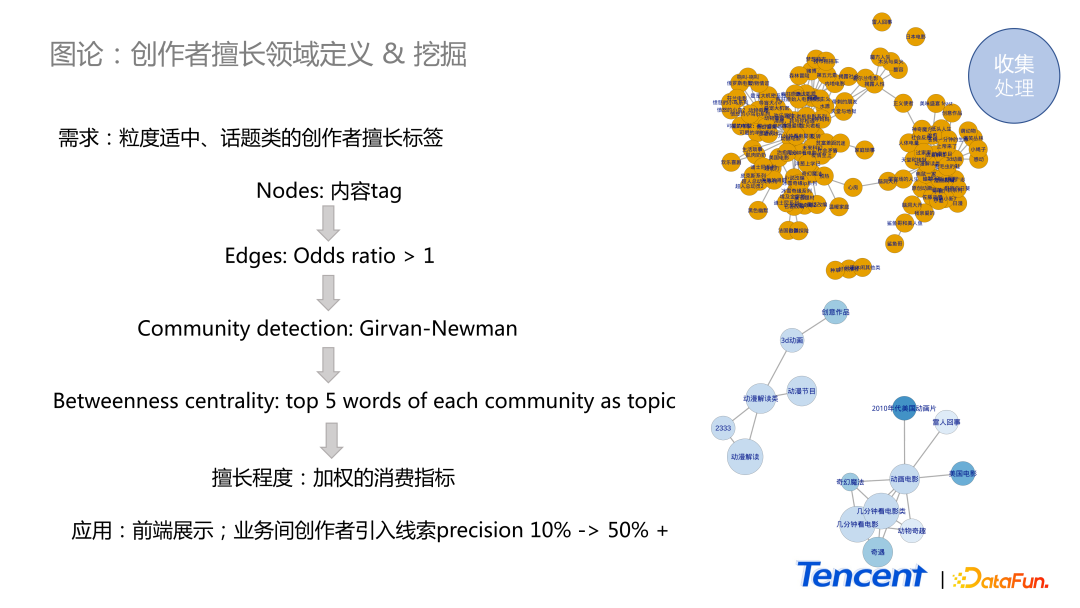
第二个例子是图论里的方法的应用，我们希望对创作者擅长的领域进行描述，并且对其擅长度进行打分。
在我们的体系里，对于创作者的内容可分成两类：
- 按类型分类，约有几百个类型。
- 按 tag 分类，至少有几百万的量级。
对于运营同学而言，几百量级的分类，颗粒度太粗，而几百万的 tag 分类， 颗粒度又太细，很难直观地描述创作者适合创作什么话题。
因此我们针对每一个创作者，将他过去一段时间内的发文的 tag 取出来。每一个 tag 作为一个节点。我们把节点 a 和节点 b 当作两个随机事件，若其中一个发生使得另一个事件更容易发生，即认为它们之间存在正相关性，在两个节点之间连上一条线。我们可以用 odds ratio 来度量这个关系，若它大于 1，就给它们之间连上线。接下来用一个比较经典的 community detection 的方法去对它进行分析。可将社区看作是创作者常创作的话题，有社区之后，我们可以找中心度比较高的词，并认为这些些词能够抽象地描述出这个话题是什么。最后，我们用一个加权的消费指标，描述在话题里作者的擅长程度。
图中黄色点是一个创作者原始的数据，下方是经过处理后最终得到的结果。可以看出，创作者擅长创作两类话题，一类是动画电影的解读，一类是动漫类作品的解读。这个结果提高了不同业务之间创作者引入索引的准确性，从 10% 提高了至 50%。
3、结算策略变化对创作者的影响
通过数据分析和算法模型，我们对创作者的基本画像有了概念，那么如何推动不同类型的创作者调整他们的行为呢？
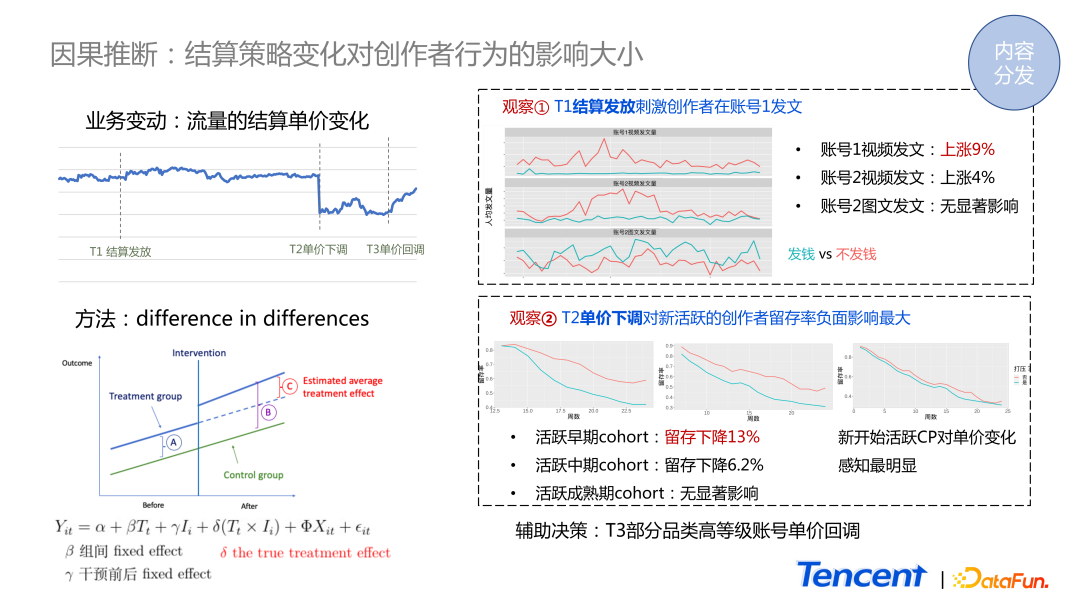
其中一个因素是结算策略的变化。我们希望知道结算策略的变化对创作者有什么影响，影响有多大。如图所示，这是某一个视频业务的账号体系的结算单价数据，从 T1 时刻开始结算发放，到 T2 时刻下调单价。我们想知道这两个行为在创作者侧产生了怎样的影响。
创作者对结算金额是非常敏感的，无法进行传统的 AB 实验，若因他属于实验组就被削减了单价，是非常不公平的。因此在这个场景下，我们只能对历史数据进行因果推断。
最经典常用的方法是 DID，受干预的组和没有受干预的组在干预之前，创作者因本身的差异，导致我们所关心的指标产生差距 A。在 intervention 发生后，这两组的差距变成了 B。在 AB 实验场景里，可能只对 intervention 发生之后的数据进行对比，得到差异值是 B。但实际上 intervention 自己本身产生的影响是 B 减去 A，所以 C 才是我们真正想知道的值。
DID 方法的应用有两种情况：
- 单纯地计算差的差。先算 B 的值，再算下 A 的值。两个相减后，再做一些统计上的 test，观察差异是否显著。如果是，说明这个 intervention 是有影响的，并且知道影响的大小。
- 第二种应用方式是把它放到一个线性回归里面。T 代表时间，intervention 会产生一个时间点。i 表示两组分别属于被干预组，还是没有受到干预的组。重点是变量 x ，我们可以把一些用户的属性数据看作 x，如账号的年纪、账号的类型等，从而将这种 intervention 的影响分析得更清楚。
右侧是我们分析的结果：
- 在 T1 时刻，账号体系 A 发放结算使得他们的视频发文量显著提升 9%，同样，另外一个账号体系的视频发文量也显著地上升，而对图文赛道却没有影响。
- 在 T2 时刻单价下调后，发现对刚开始活跃的新账号创作者而言，他们的体感是最强的，其留存率下降 13%。而对于活跃中期的用户，留存的下降就没那么明显，而成熟期的基本没有产生影响。
这两个观察结论辅助了业务进行决策，决定在 T3 时刻对部分的高等级账号进行单价的回调。
四、问答环节
Q1：在日常的生活工作中，基于分布给出估计的前提是我们知道数据符合什么样的分布。在无法直观判断分布的前提下，我们应该怎么处理数据，使其可以满足我们后续预测的需求？
A1：首先都会有一个直观的感受。比如我们可以先画下 Histogram，大概看一下它长成什么形状。大多数情况下，这些分布是有参数的，如正态是有参数的，这些 power law也是有参数的。我们可以用 maximum likelihood 对参数进行估计，然后用这些参数可以做一个 simulation，查看这个分布下产生的数据是什么样子的。相当于我们有了两组数据，进而我们又可以做 Kolmogorov Smirnov test，查看两组分布是否存在显著的差异。如果没有显著的差异，即证明我们 calibrate 出来分布能满足所需。
但实际中常出现一种情况，如上面所提到的例子，一般 log normal 和 Power Law 上最后的结果都差不多。所以在这种情况下，不管是用 log normal 还是用 Power Law 都可以。
Q2：请问对于符合 Power Law 分布的总体来说，在后续建模中，如果过分提高头部样本的权重，对长尾部分样本的权益存在一定的不公平，在实际业务中会引起长尾用户的反感。该如何规避建模时这种情况的发生呢？
A2：实际上，在我们的业务里，前期在做数据分析时并不会规避这些东西。比如想找到哪些相对不重要的内容，我们就会认认真真地做分析找出结论。但在做策略时，会考虑这些问题，在策略的设计上做得比较温和。
