基本思想
先来回顾一下直接插入排序的算法思想,就是在前面已经排好序的子序列中寻找一个待插入的位置,然后将待插入元素插入到该位置上。
其中寻找插入位置的过程我们是与每一个元素进行比较,相当于顺序查找,我们知道顺序查找的效率是比较低的,那么有没有办法能够提高查找插入位置的效率呢?
很巧的是,前面的序列既然已经是有序的了,我们何不采用折半查找来找出插入位置呢?折半查找的前提就是序列有序,采用折半查找法查找插入位置的插入排序算法,我们称其为折半插入排序。
图解排序过程
折半插入算法非常简单,前提你得掌握直接插入排序和折半查找的算法,来看一个例子:
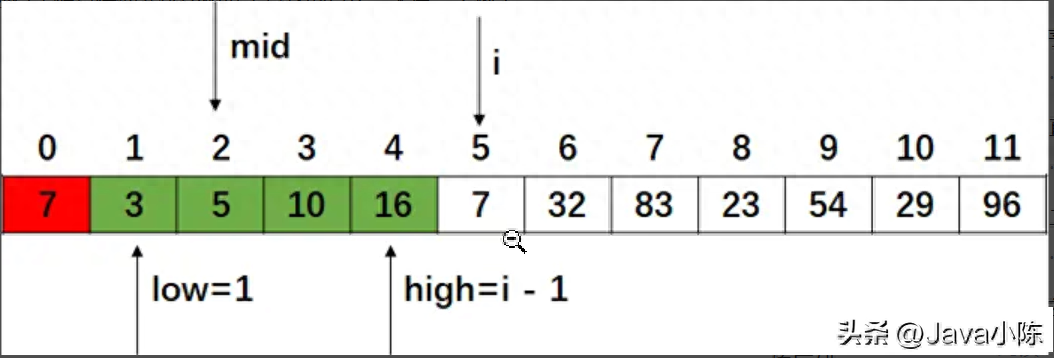
原序列的前四个元素已经有序,则从i位置元素开始进行插入排序,先将i位置元素存入下标0作为哨兵,然后在子序列中寻找待插入位置。
这时我们可以采用折半查找法进行查找,定义三个变量low、high和mid,初始low = 1,high = i -1,则mid为2。
让哨兵位置元素值与mid位置元素值比较,7大于5,所以插入位置应该在右半区,让low = mid + 1,high不变,继续折半查找:
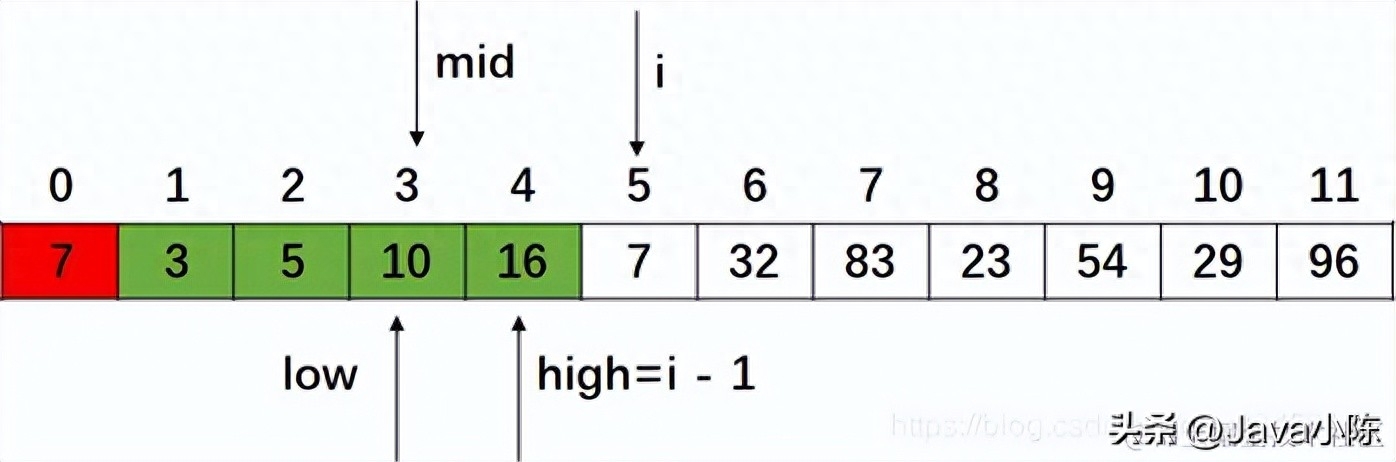
7小于10,则插入位置应该在左半区,让high = mid - 1,low不变:
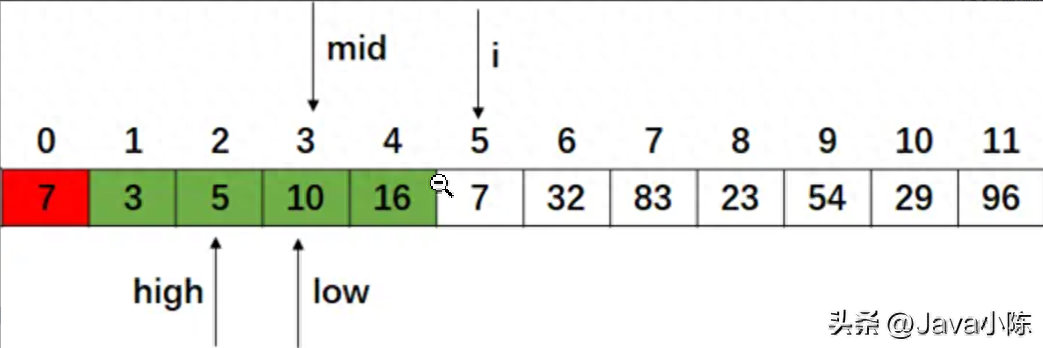
此时high大于low,查找结束,则插入位置即为high + 1,这些都是折半查找的内容,这里不赘述。
找到了插入位置为high + 1,可不能直接将待插入元素值存入high + 1位置,这样会覆盖原先的元素值,而应该从high + 1位置开始,到i - 1位置为止,将该范围内的所有元素后移,空开high + 1位置,最后将哨兵位置元素插入到high + 1位置即可。
代码实现
先构建待排序序列:
public class ElemType {
int key;
}
public class SSTable {
ElemType[] n;
int length;
public SSTable() {
this.length = 11;
this.n = new ElemType[this.length + 1];
for (int i = 1; i <= this.length; i++) {
this.n[i] = new ElemType();
}
this.n[1].key = 3;
this.n[2].key = 5;
this.n[3].key = 10;
this.n[4].key = 16;
this.n[5].key = 7;
this.n[6].key = 32;
this.n[7].key = 83;
this.n[8].key = 23;
this.n[9].key = 54;
this.n[10].key = 29;
this.n[11].key = 96;
}
}折半插入排序算法如下:
public class Main {
public static void BInsertSort(SSTable t) {
int i, j, low, high, mid;
//从第二个元素开始插入排序
for (i = 2; i <= t.length; ++i) {
//将待插入元素存入哨兵位置
ElemType temp = t.n[i];
//为low和high赋初值
low = 1;
high = i - 1;
while (low <= high) {
mid = (low + high) / 2;
if (temp.key < t.n[mid].key) {
high = mid - 1;
} else {
low = mid + 1;
}
}
//将high + 1到i - 1的元素后移
for (j = i - 1; j >= high + 1; --j) {
t.n[j + 1] = t.n[j];
}
//将哨兵位置元素插入j + 1位置
t.n[j + 1] = temp;
}
}
public static void main(String[] args) {
SSTable st = new SSTable();
BInsertSort(st);
}
}性能分析
可以肯定的是,折半插入排序的效率是要高于直接插入排序的,它所需要的关键码比较次数与待排序对象序列的初始排列无关,仅依赖于对象个数。在插入第i个对象时,需要经过「log2i」 + 1次关键码比较才能确定插入位置。