本文将介绍3个在数据集中查找离群值的Python方法。
离群值(Outliers)是指在数据集中与其他数据点明显不同或者异常的数据点。这些数据点可能比其他数据点要远离数据集的中心,或者具有异常的数值。离群值可能是由于数据采集错误、异常事件、测量误差或者其他未知因素引起的。

离群值的存在可以对数据分析和统计建模产生重要影响,因为它们可能导致模型不准确或者产生误导性的结果。
我们先创建一个演示的数据
import pandas as pd
import matplotlib.pyplot as plt
name = ['John', 'Victor', 'Carlos', 'Leo', 'Kevin', 'Silva', 'Johnson', 'Lewis', 'George', 'Daniel', 'Harry', 'Jordan', 'James']
salary = [4000, 1000, 2000, 100000, 3500, 6000, 1500, 3000, 2500, 3600, 2100, 1700, 1600]
df = pd.DataFrame({'Name': name, 'Salary': salary})
plt.boxplot(df['Salary'])
plt.show()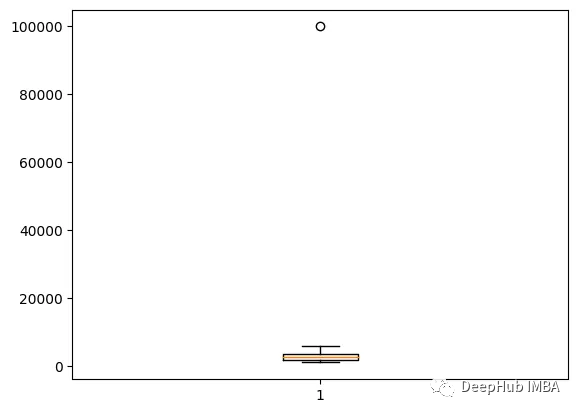
可以看到上面的点就是离群值,下面我们将介绍快速找到它的方法。
四分位极差法
首先找到第一和第三个四分位数值,通常记为Q1和Q3。然后用Q3减去Q1计算四分位差(IQR)。
通过减去/增加1.5倍IQR来计算下界和上界。上下边界外的值就是离群值
q1 = df['Salary'].quantile(0.25)
q3 = df['Salary'].quantile(0.75)
iqr = q3 - q1
lower_bound = q1 - 1.5 * iqr
upper_bound = q3 + 1.5 * iqr
outliers = df[(df['Salary'] < lower_bound) | (df['Salary'] > upper_bound)]1.5倍IQR的阈值通常是一种常用的标准,阈值的选择可以根据具体情况进行调整。有时候,也可以选择更严格或更宽松的阈值,以适应特定的数据分析需求。
标准偏差法
标准偏差法(Standard Deviation Method)使用数据的标准差来判断数据点是否偏离了数据。上界和下界是均值和3倍标准差的加减。
他的方法如下:
计算平均值和标准偏差: 首先,计算数据的平均值(Mean)和标准偏差(Standard Deviation)。平均值代表了数据的中心位置,标准偏差衡量了数据的分散程度。
确定阈值: 定义一个阈值,通常是标准偏差的倍数(通常为2或3倍标准偏差)。这个阈值决定了什么样的数据点被认为是离群值。
识别离群值: 计算每个数据点与平均值之间的差值,然后将这个差值与阈值比较。如果差值超过了阈值,数据点被认为是离群值。
mean = df.Salary.mean()
std = df.Salary.std()
upper_bound = mean + 3 * std
lower_bound = mean - 3 * std
outliers = df[(df['Salary'] < lower_bound) | (df['Salary'] > upper_bound)]标准偏差法的优点在于简单易懂,而且不需要假设数据分布的形状。但需要注意以下几点:
- 通常情况下,阈值使用2或3倍标准偏差作为阈值,但这个值可能需要根据具体情况进行调整。
- 这种方法对于正态分布的数据集效果较好,但对于偏斜分布的数据,可能会导致误判。
- 标准偏差法可能不适用于小样本,因为标准偏差在小样本中可能不够稳定。
Z-分数法
Z-分数(Z-Score)法测量了数据点与数据集平均值之间的偏差,以标准化方式表示这个偏差。对于每个数据点,计算它与平均值之间的差值,然后将这个差值除以标准偏差,得到Z-分数。如果z-score大于3.0或小于-3.0,则该值可归类为离群值。
我们可以直接使用scipy提供的函数来进行计算
from scipy import stats
df['Salary_zscore'] = stats.zscore(df['Salary'])
filtered_df = df[(df['Salary_zscore'] <= 3) & (df['Salary_zscore'] >= -3)]Z-分数法适用于各种类型的数据分布,不需要假设数据分布的形状。并且提供了标准化的度量,使得不同数据集之间的离群值比较更加容易。
总结
以上是可以快速找到离群值的统计学方法,除此以外,还有一些机器学习的方法例如:
DBSCAN(Density-Based Spatial Clustering of Applications with Noise): DBSCAN是一种密度聚类算法,也可用于检测离群值。它根据数据点的密度来识别离群值,将密度较低的点视为离群值。
LOF(Local Outlier Factor): LOF是一种局部离群值因子方法,用于检测局部区域内的离群值。它考虑了每个数据点周围的局部密度与相邻点的密度之间的比率,从而识别离群值。
Isolation Forest: Isolation Forest是一种基于随机森林的离群值检测方法,它通过构建树结构来识别离群值。由于使用了随机性,它对高维数据和大数据集非常有效。
但是这些方法执行的速度会很慢,如果对于速度要求比较严格还是需要谨慎选择。






























