数学推理是现代大型语言模型(LLM)的一项关键能力。尽管这一领域近来进展不错,但闭源和开源 LLM 之间仍然存在明显的差距——GPT-4、PaLM-2 和 Claude 2 等闭源模型主宰了 GSM8K 和 MATH 等常用数学推理基准,而 Llama、Falcon 和 OPT 等开源模型在所有基准上都大幅落后。
为了解决这一问题,研究界正在两个方向进行努力:
(1)Galactica 和 MINERVA 等持续型预训练方法,其能在超过千亿 token 的数学相关网络数据上对 LLM 进行持续训练。这一方法能提升模型的一般科学推理能力,但代价是高计算成本。
(2)拒绝采样微调(RFT)和 WizardMath 等针对特定数据集进行微调的方法,即使用特定数据集的监督数据对 LLM 进行微调。尽管这些方法能提升在具体领域内的性能,但无法泛化到微调数据之外的更广范围的数学推理任务。举个例子,RFT 和 WizardMath 可将在 GSM8K(这是微调数据集之一)上的准确度提升 30% 以上,但却有损在 MMLU-Math 和 AQuA 等领域外数据集上的准确度——使之降低多达 10%。
近日,来自滑铁卢大学和俄亥俄州立大学等机构的研究团队提出了一种轻量级却又可泛化的数学指令微调方法,可用于增强 LLM 的一般性(即不限于微调任务)数学推理能力。
之前已有的方法关注的重点是思维链(CoT)方法,即通过一步步的自然语言描述来解决数学问题。这种方法的通用性很强,可覆盖大多数数学科目,但却在计算精度和复杂的数学或算法推理过程(例如求解二次方程根和计算矩阵特征值)方面存在困难。
相比之下,像思维程序(PoT)和 PAL 这样的代码格式 prompt 设计方法则是利用外部工具(即 Python 解释器)来大幅简化数学求解过程。这种方法是将计算过程卸载到外部 Python 解释器来求解复杂的数学和算法推理(例如使用 sympy 求解二次方程或使用 numpy 计算矩阵特征值)。但是,PoT 难以应对更抽象的推理场景,比如常识推理、形式逻辑和抽象代数,尤其是没有内置的 API 时。
为了取 CoT 和 PoT 两种方法之长,该团队引入了一个新的数学混合指令微调数据集 MathInstruct,其有两大主要特性:(1) 广泛涵盖不同的数学领域和复杂程度,(2) 将 CoT 和 PoT 原理组合到了一起。
MathInstruct 基于七个现有的数学原理数据集和六个新整理出的数据集。他们使用 MathInstruct 微调了不同大小(从 7B 到 70B)的 Llama 模型。他们将所得到的模型称为 MAmmoTH 模型,结果发现 MAmmoTH 的能力是前所未有的,就像是一个数学通才。
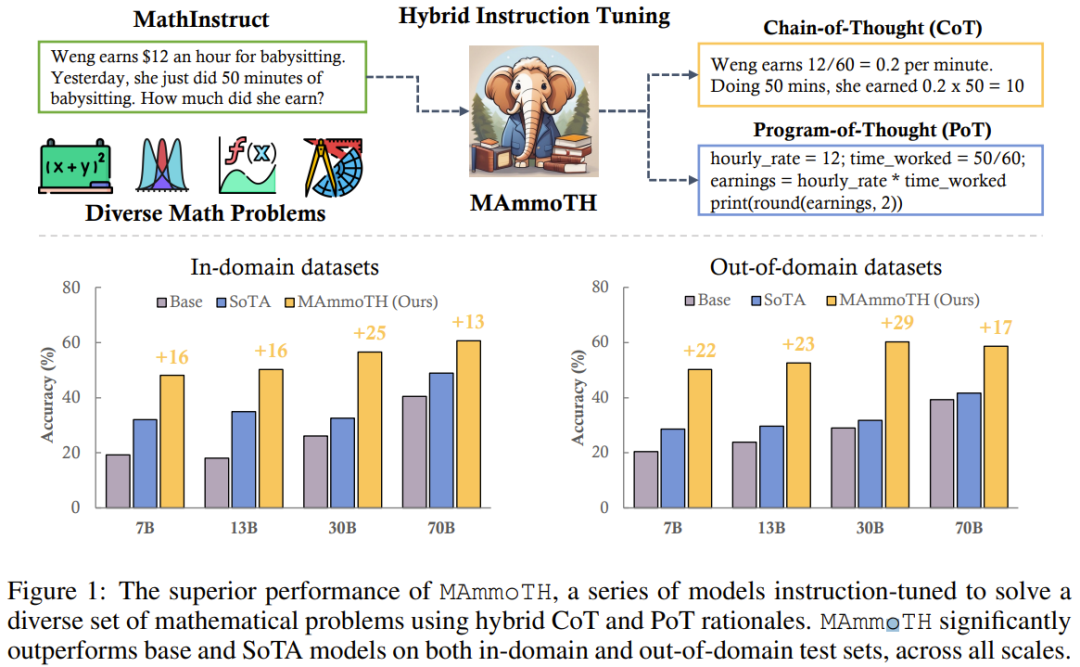
为了评估 MAmmoTH,该团队使用了一系列评估数据集,包括领域内的测试集(GSM8K、MATH、AQuA-RAT、NumGLUE)和领域外的测试集(SVAMP、SAT、MMLU-Math、Mathematics、SimulEq)。
结果发现,相比于之前的方法,MAmmoTH 模型能更好地泛化用于领域外数据集,并能大幅提升开源 LLM 的数学推理能力。
值得注意的是,在常用的竞赛级 MATH 数据集上,7B 版本的 MAmmoTH 模型能以 3.5 倍的优势(35.2% vs 10.7%)击败 WizardMath(这是 MATH 上之前最佳的开源模型),而 34B MAmmoTH-Coder(在 Code Llama 上进行过微调)甚至可以胜过使用 CoT 的 GPT-4。
这项研究的贡献可以总结成两个方面:(1) 从数据工程方面看,他们提出了一个高质量的数学指令微调数据集,其中包含多种不同的数学问题和混合原理。(2) 从建模方面讲,他们训练和评估了大小从 7B 到 70B 的 50 多个不同的新模型和基准模型,以此探究了不同数据源和输入-输出格式的影响。
结果发现,MAmmoTH 和 MAmmoTH-Coder 等新模型在准确度方面都显著优于之前的开源模型。

- 论文:https://arxiv.org/pdf/2309.05653.pdf
- 代码:https://github.com/TIGER-AI-Lab/MAmmoTH
- 数据集与模型:https://huggingface.co/datasets/TIGER-Lab/MathInstruct
该团队已经发布了他们整理得到的数据集,并开源了新方法的代码,也在 Hugging Face 发布了训练好的不同大小的模型。
新提出的方法
整理一个多样化的混合指令微调数据集
该团队的目标是编制一份列表,其中包含高质量且多样化的数学指令微调数据集,其应具有两个主要特征:(1) 广泛涵盖不同的数学领域和复杂程度,(2) 将 CoT 和 PoT 原理组合到一起。
对于第一个特征,他们首先选出了一些使用广泛并且涉及不同数学领域和复杂程度的高质量数据集,比如 GSM8K、MATH、AQuA、Camel 和 TheoremQA。然后他们注意到现有数据集没有大学水平的数学知识,比如抽象代数和形式逻辑。针对这个问题,他们借助于网上找到的少量种子示例,使用 GPT-4 为 TheoremQA 中的问题合成 CoT 原理并通过 Self-Instruct 创建「问题-CoT」配对。
对于第二个特征,将 CoT 和 PoT 原理组合到一起可以提升数据集的多功能性,使其训练的模型有能力解决不同类型的数学问题。但是,大多数现有数据集提供的程序原理有限,导致 CoT 和 PoT 原理之间不平衡。为此,该团队又用到了 GPT-4,来为所选数据集补充 PoT 原理,包括 MATH、AQuA、 GSM8K 和 TheoremQA。然后再对这些 GPT-4 合成的程序进行过滤,做法是将它们的执行结果与人类标注的基本真值进行比较,这能确保所添加的都是高质量的原理。
遵循这些准则,他们创建了一个新的数据集 MathInstruct,详见下表 1。
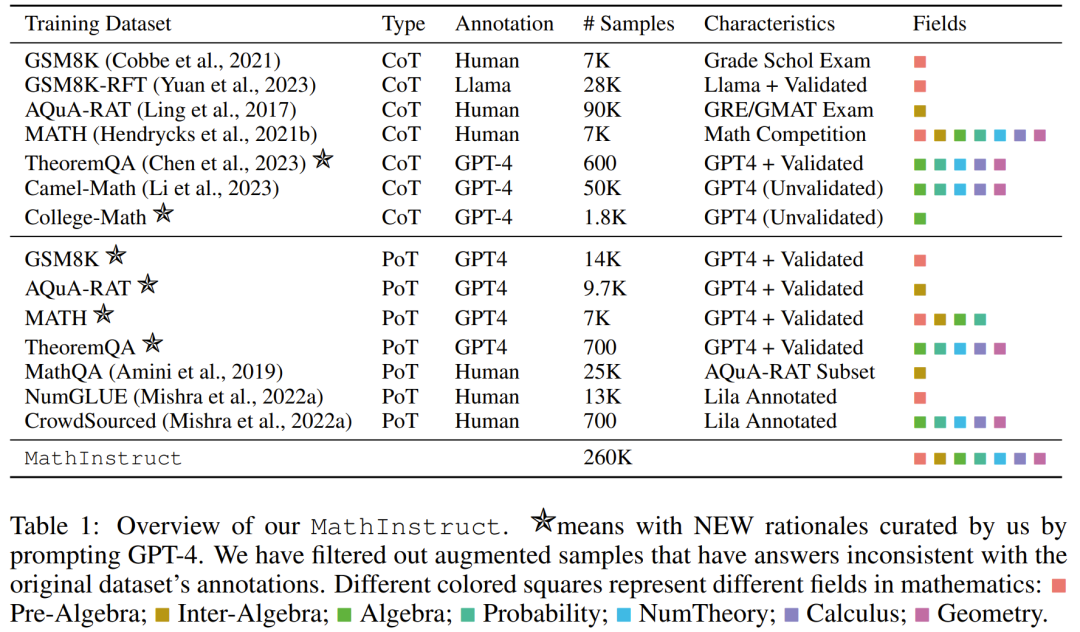
其中包含 26 万对 (指令,响应),覆盖广泛的核心数学领域(算术、代数、概率学、微积分和几何等),包含混合的 CoT 和 PoT 原理,并有不同的语言和难度。
训练设置
MathInstruct 的所有子集都统一成了类似 Alpaca 的指令数据集的结构。这种标准化操作可确保微调得到的模型能够一致地处理数据,无论原始数据集格式如何。
在基础模型方面,该团队的选择是 Llama-2 和 Code Llama。
通过在 MathInstruct 上进行微调,他们得到了 7B、13B、34B 和 70B 等大小不同的模型。
实验
评估数据集
为了评估模型的数学推理能力,该团队选择了一些评估数据集,见下表 2,其中包含许多不同领域内和领域外样本,涉及多个不同数学领域。
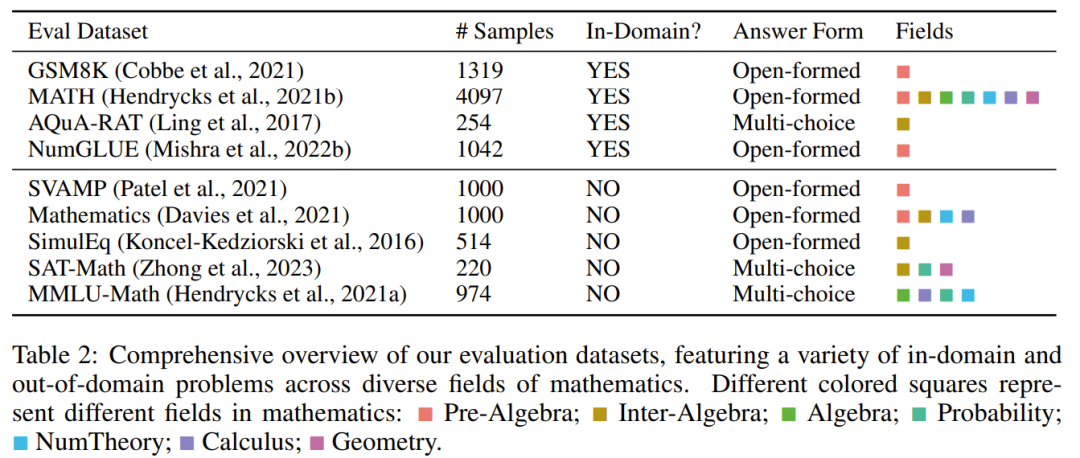
这个评估数据集也包含不同的难度等级,包括小学、中学和大学水平。某些数据集甚至包括形式逻辑和常识推理。
所选择的评估数据集既有开放式问题,也有多项选择题。
对于开放式问题(如 GSM8K 和 MATH),研究者采用了 PoT 解码,因为大多数这类问题可以通过程序求解。、
对于多项选择题(如 AQuA 和 MMLU),研究者采用了 CoT 解码,因为这个数据集中的大部分问题都可以通过 CoT 更好地处理。
CoT 解码不需要任何触发词,而 PoT 解码需要一个触发语:「Let’s write a program to solve the problem」。
主要结果
下表 3 和表 4 分别报告了在领域内外数据上的结果。
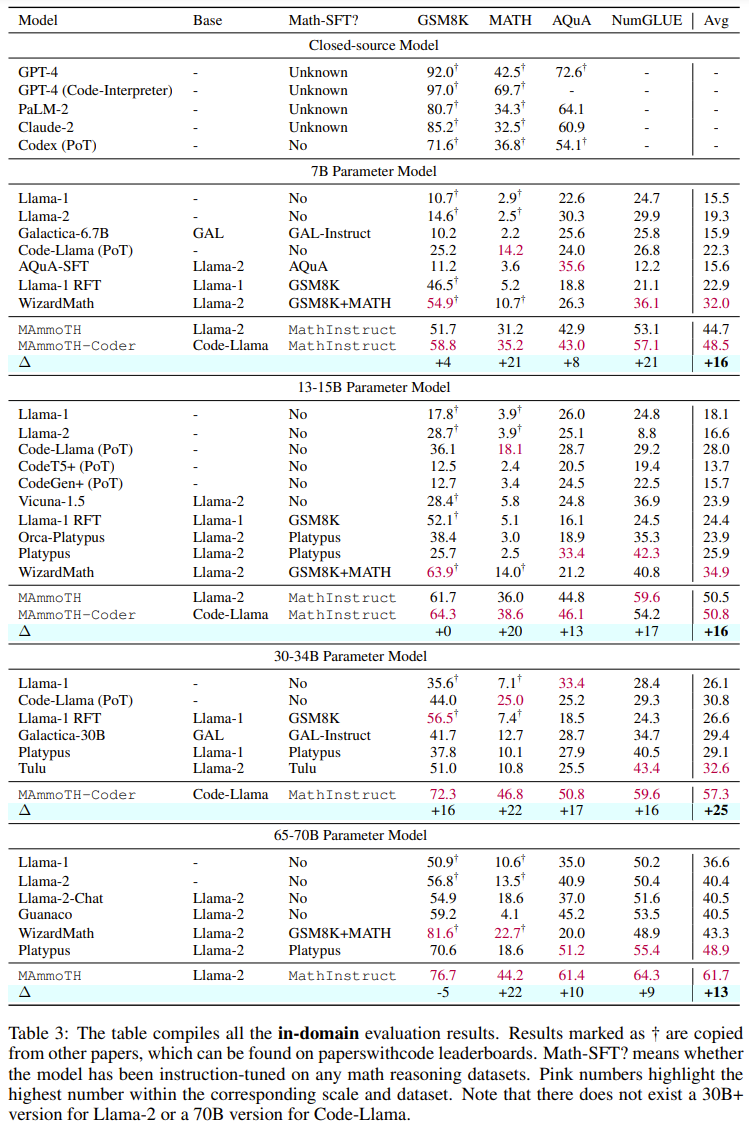

总体而言,在不同的模型大小上,MAmmoTH 和 MAmmoTH-Coder 都优于之前最佳的模型。新模型在领域外数据集上取得的性能增长多于在领域内数据集上所获增长。这些结果表明新模型确实有成为数学通才的潜力。MAmmoTH-Coder-34B 和 MAmmoTH-70B 在一些数据集上的表现甚至超过了闭源 LLM。
研究者也比较了使用不同基础模型的情况。具体来说,他们实验了 Llama-2 和 Code-Llama 这两种基础模型。从上面两张表可以看出,Code-Llama 整体上要优于 Llama-2,尤其是在领域外数据集上。MAmmoTH 和 MAmmoTH-Coder 之间的差距甚至可达 5%。
在数据源上的消融研究
他们通过消融研究探索了性能增益的来源。为了更好地理解 MAmmoTH 相对于已有基准模型的优势的来源,研究者进行了一系列对照实验,结果如下图 2 所示。
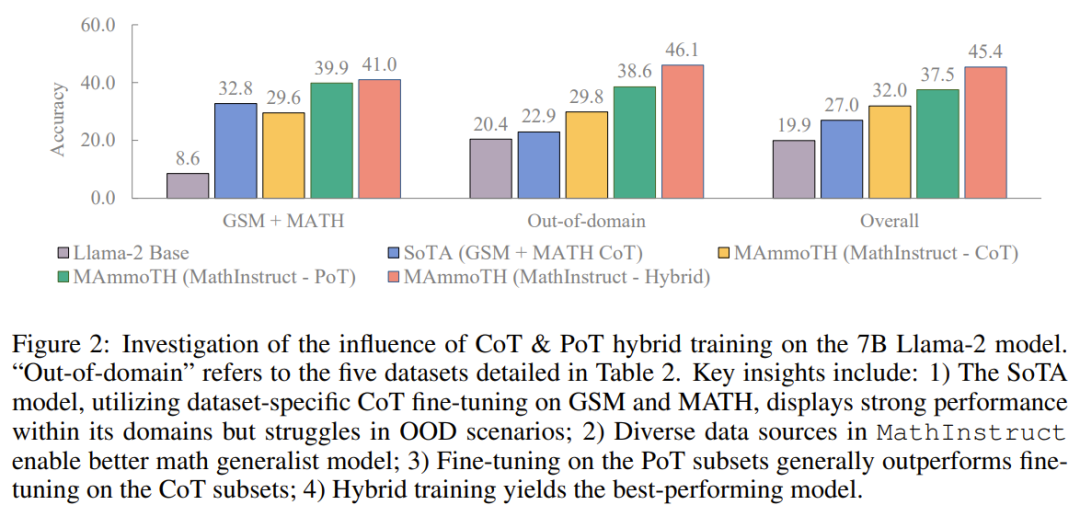
总结起来,MAmmoTH 的显著性能优势可以归功于:1) 涵盖不同的数学领域和复杂程度的多样化数据源,2) CoT 和 PoT 指令微调的混合策略。
他们也研究了主要子集的影响。对于用于训练 MAmmoTH 的 MathInstruct 的多样化来源,理解各个来源对模型整体性能的贡献程度也很重要。他们关注的重点是四个主要子集:GSM8K、MATH、 Camel 和 AQuA。他们进行了一项实验:逐渐将每个数据集添加到训练中,并将性能与在整个 MathInstruct 上微调的模型进行比较。
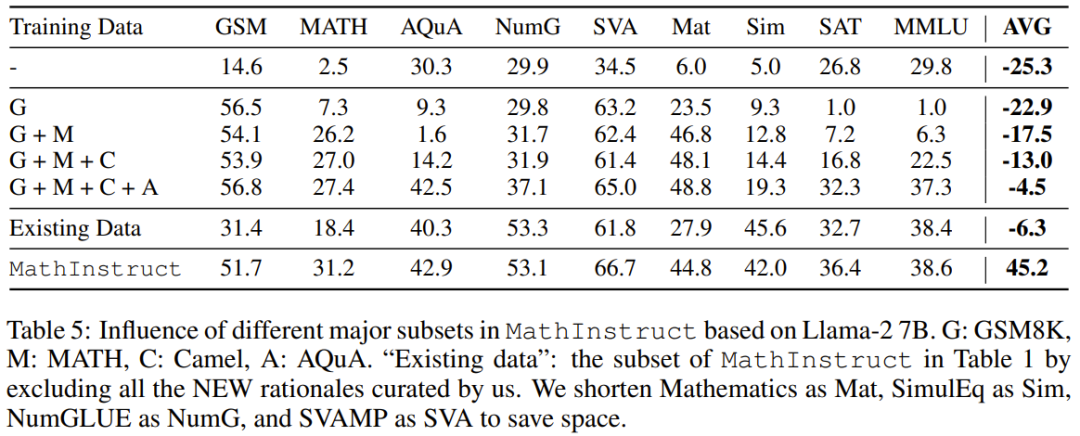
从表 5 的结果可以看到,如果一开始训练的数据集不够多样化(比如只有 GSM8K 时),整体的泛化能力非常差:模型只拟合了分布内的数据,难以解答 GSM 问题之外的问题。
这些结果凸显了多样化数据源对 MAmmoTH 的重要影响,它们是让 MAmmoTH 成为数学通才的核心关键。这些结果也贡献了宝贵的见解,能为我们未来的数据整理收集工作提供指导比如我们应该总是收集多样化的数据,避免只收集特定类型的数据。

































