当前,大型语言模型 (LLM) 在处理 NLP 领域的各种下游任务方面已经表现出卓越的能力。特别是,GPT-4、ChatGPT 等开创性模型已经接受了大量文本数据的训练,使它们具备强大的文本理解和生成能力,能够生成连贯且上下文相关的响应,在各种 NLP 任务中具有高度通用性。
然而,LLM 在数学推理方面的性能却不尽如人意。LLM 很难准确地执行复杂的算术运算,尤其是涉及超过 8 位数字乘法的运算,还有涉及小数、分数的运算。
基于此,来自清华大学、TAL AI Lab 和智谱 AI 的研究者联合提出了一个能够完美执行复杂算术运算的新模型 ——MathGLM。

- 论文地址:https://arxiv.org/pdf/2309.03241v2.pdf
- 项目地址:https://github.com/THUDM/MathGLM#arithmetic-tasks
该研究表明:在足够的训练数据下,20 亿参数的语言模型能够准确地进行多位算术运算,准确率几乎达到了 100%,且不会出现数据泄露(data leakage)。这个结果大幅超越了 GPT-4(其多位乘法运算准确率仅为 4.3%)。
方法介绍
本文提出了一个名为 MathGLM 的模型来探讨 LLM 在数学推理方面的效率。
MathGLM 模型需要完成的算术任务大致可以分为两类:基本算术运算和复杂混合运算。其中基本算术运算包含基本的数学任务,这些任务围绕两个数字的简单计算。而复杂混合运算涉及不同算术运算和数字格式(例如整数、小数、分数等)的组合。表 1 为 MathGLM 任务分类。
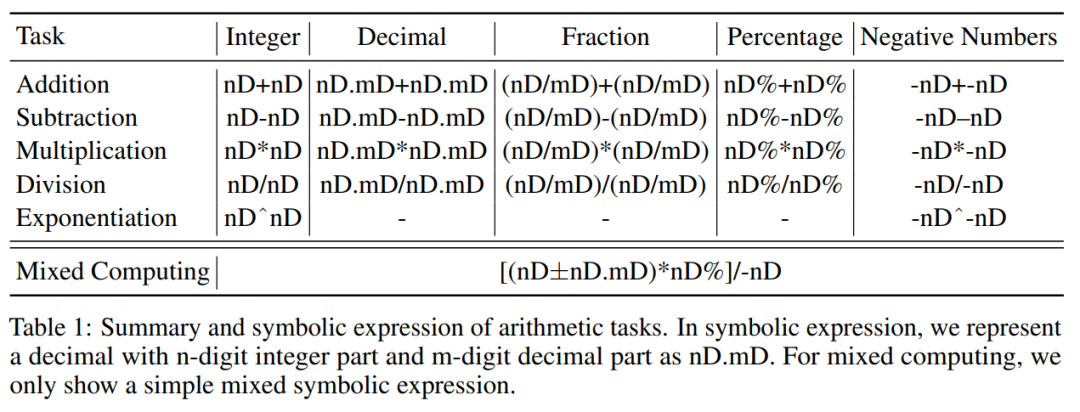
为了增强 MathGLM 的算术能力,本文采用了基于 Transformer 的仅解码器架构,并使用自回归目标(autoregressive objective)在生成的算术数据集上从头开始训练它。
算术任务的学习
算术训练数据集是精心设计的,包括加法、减法、乘法、除法和求幂等多种运算。此外,它还包含多种数字格式,例如整数、小数、百分比、分数和负数。数据集规模大小不一,范围从 100 万到 5000 万条记录不等。
在每个数据集中,单个算术表达式由 2 到 10 个运算步骤组成,涵盖一系列数学运算,例如加法 (+)、减法 (-)、乘法 (×)、除法 (/) 和求幂 (^)。图 3 为从算术数据集中提取的一些训练示例:

表 2 概述了 MathGLM 模型的不同规模,包括 4 种不同类型的模型,每种模型都有不同的参数大小。最大的模型参数量为 2B,容量最强;其余参数量分别为 500M 、100M 以及最小的 10M 参数模型。
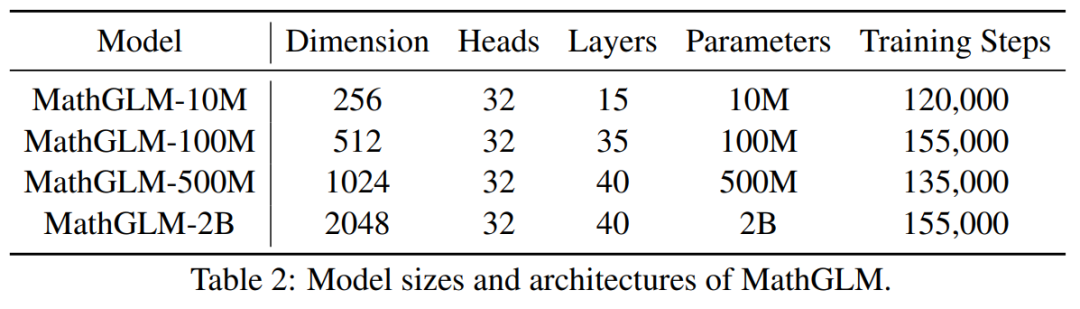
对数学应用问题的学习
除了算术任务外,本文还训练(微调)了一系列基于 Transformer 的语言模型,称为通用语言模型 (GLM,General Language Model)及其聊天版本来解决数学应用问题。训练过程使用了公开的 Chinese Ape210K 数据集,该数据集包含 21 万道中文小学数学题,每个题的答案都是直接计算得出的。
为了提高 MathGLM 在数学应用题上的性能,本文采用分步策略来重建 Ape210K 数据集,并将其转换为逐步计算每个数学问题答案的版本。图 4 展示了原始 Ape210K 数据集和本文重建版本之间的对比。

本文采用 GLM 的不同变体作为骨干来训练 MathGLM,包括具有 335M 参数的 GLM-large、GLM-6B、GLM2-6B 和 GLM-10B。此外,本文还使用 ChatGLM-6B 和 ChatGLM2-6B 主干网络训练 MathGLM。这些骨干模型赋予 MathGLM 基本的语言理解能力,使其能够有效理解数学应用题中包含的语言信息。
实验
本文设计了两种不同类型的实验,包括算术任务和数学应用题。
对于算术任务,本文预训练了一个基于 Transformer 的 MathGLM 模型,该模型具有 500M 参数,并将其与领先的大型语言模型 (LLM)(例如 GPT-4 和 ChatGPT)的性能进行了比较。结果如表 3 所示, MathGLM 优于所有其他模型,表明 MathGLM 在处理算术任务方面具有卓越的性能。
即使只有 1000 万个参数的 MathGLM-10M,结果也令人惊讶。MathGLM-10M 在一系列综合算术任务中的性能优于 GPT-4 和 ChatGPT。
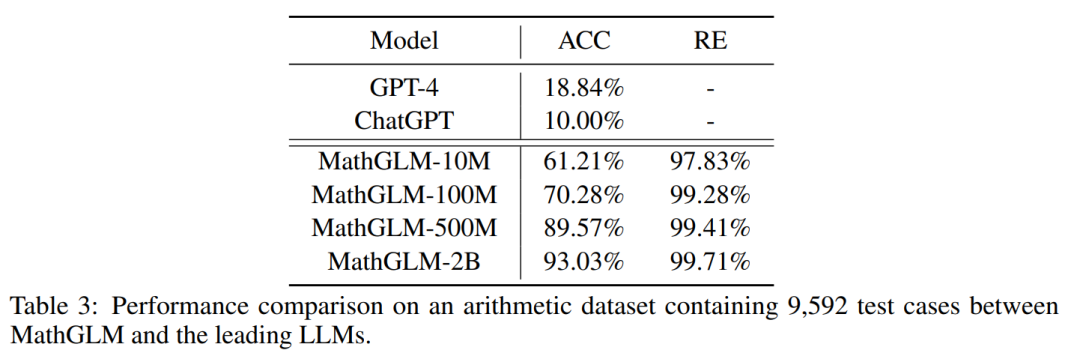
此外,当比较不同参数规模的 MathGLM 时,本文观察到 MathGLM 的算术性能与其参数数量的增加直接相关。这一发现表明,随着模型尺寸的增加,它们的性能表现出相应的增强。
综上所述,研究者对复杂算术任务的评估结果表明 MathGLM 具有卓越的性能。通过分解算术任务,这些模型的性能显著超过了 GPT-4 和 ChatGPT。
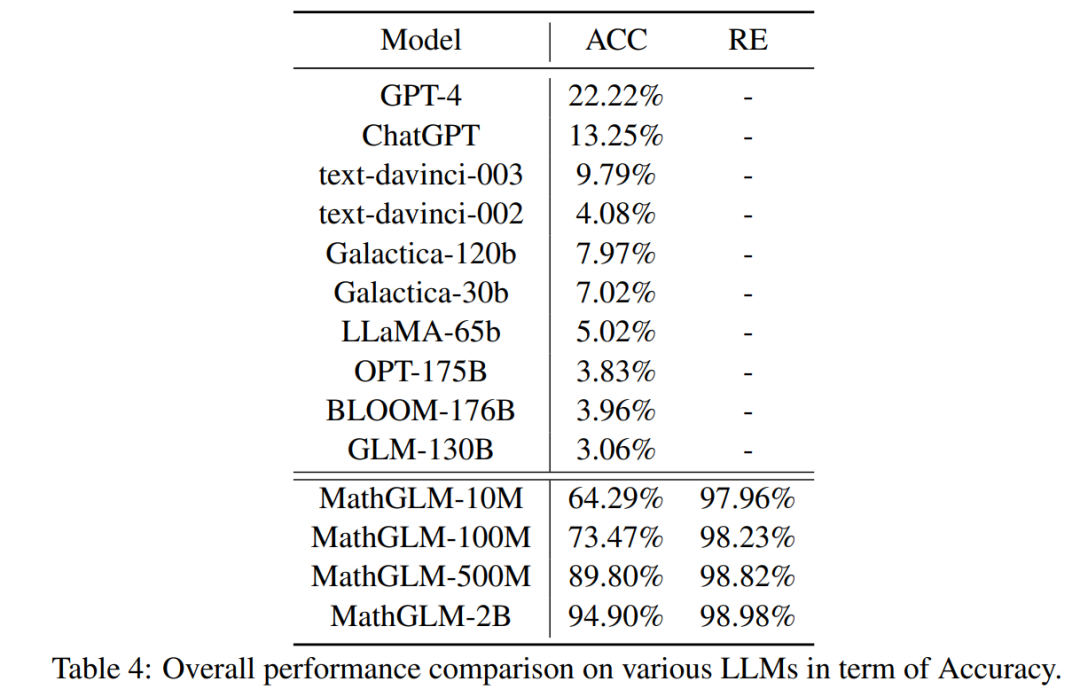
此外,本文还对 GPT-4、ChatGPT、text-davinci-003、code-davinci-002、Galacica、LLaMA、OPT、BLOOM 和 GLM 进行了比较。本文从前面讨论的大数据集中随机抽取了一个包含 100 个测试用例的紧凑算术数据集。结果如表 4 所示。
通过以上分析结果可以看出,MathGLM 在 20 亿参数下达到了 93.03% 的准确率,超越了所有其他 LLM。
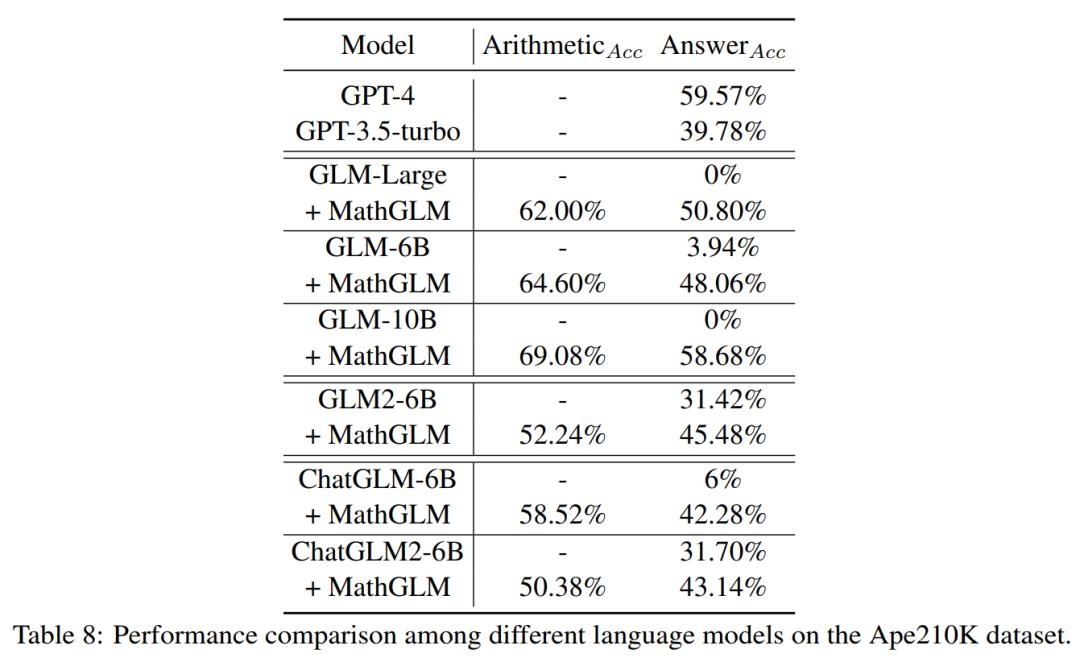
对于数学应用问题,本文在 Ape210K 数据集上进行了实验。表 8 报告了包括 MathGLM 变体、 GPT-4、ChatGPT 等在内的结果。
结果表明,当与 GLM-10B 配合使用时,MathGLM 在答案准确性方面达到了与最先进的 GPT-4 模型相当的性能水平。
此外,将 MathGLM 的性能与 GLM-Large、GLM-6B 和 GLM-10B 进行比较时,出现了一个明显的趋势:MathGLM 在算术准确性和答案准确性方面都表现出显著增强。
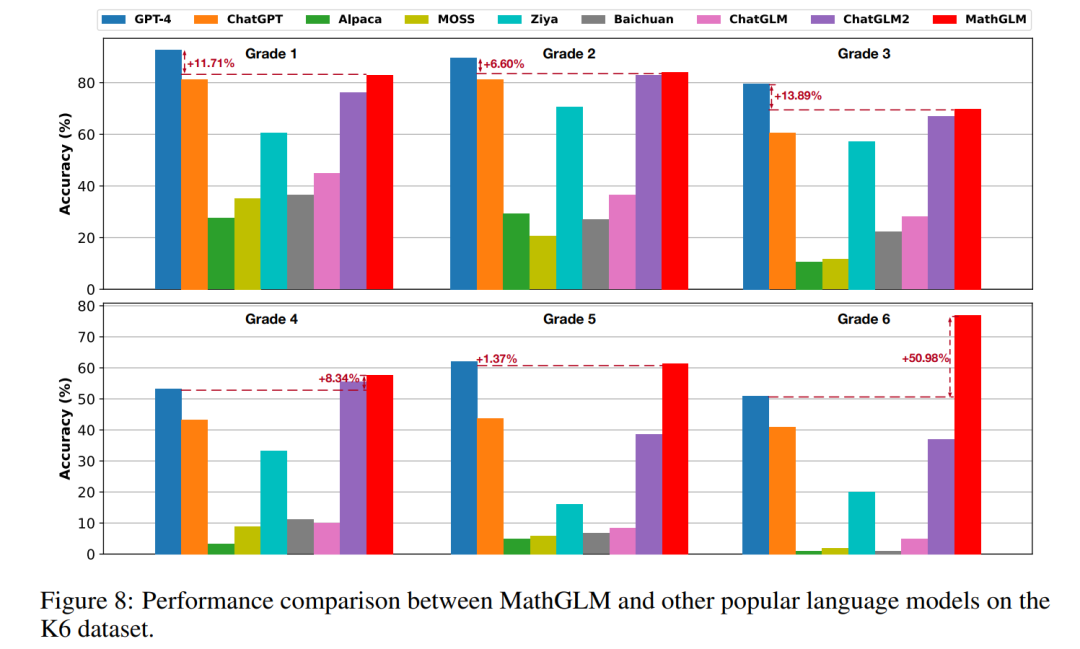
为了评估模型在不同年级数学问题上的解决能力,该研究在 K6 数据集上测试评估了几种模型的性能,包括:GPT-4、ChatGPT、Chinese-Alpaca-13B、MOSS-16B、Ziya-LLaMA-13B、Baichuan-7B、ChatGLM-6B、ChatGLM2-6B 和 MathGLM-GLM-10B,结果如下图 8 所示。
感兴趣的读者可以阅读论文原文,了解更多研究内容。











































