大语言模型，果然可以用来研究数学定理！
最近，微软亚洲研究院、北大、北航等机构的研究人员，通过97个回合的「苏格拉底式」严格推理，成功让GPT-4得出了「P≠NP」的结论！
论文地址：https://arxiv.org/abs/2309.05689
几个月前，数学天才陶哲轩曾在一篇博客中称，2026年，AI将与搜索和符号数学工具相结合，成为数学研究中值得信赖的合著者。
6月，加州理工、英伟达、MIT等机构的学者，就构建了一个基于开源LLM的定理证明器LeanDojo。
如今，GPT-4用出色的表现再次证明，LLM的确有进行科学研究和科学发现的能力。
P/NP难题有多难
作为美国克雷数学研究所（CMI）在2000年公布的七个千禧年难题之一，「P/NP问题」目前依然是理论信息学中计算复杂度理论领域里的未解之谜。
人们喜欢把它描述为「很可能是位居理论计算机科学核心的未解决问题」，也是人类提出的最深刻的问题之一。如果解决解决P/NP难题，将彻底改变人类文明进程。
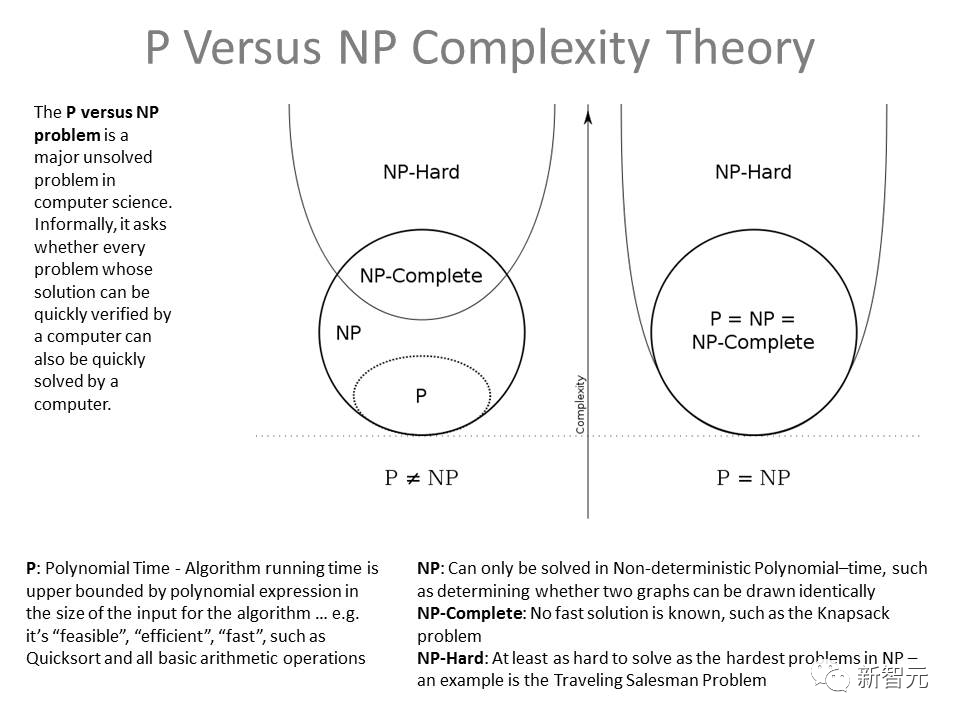
1971年，数学家Stephen A. Cook和Leonid Levin相对独立地提出这个问题：两个复杂度类P和NP是否是恒等的？
具体来说，一些永远无法通过简单计算得到答案的问题，就属于P/NP问题。
一个复杂问题如果能在多项式时间内解决，就被称为P问题，意味着计算机很容易将它求解。
那NP问题就是除了P问题之外的问题吗？未必。我们并不能证明一个问题能在多项式时间内解决，也无法证明它不能在多项式时间内解决。
所以，NP问题并不是非P类问题。
听起来似乎很复杂，我们可以用集水浒英雄卡的故事来类比。二十多年前集过卡的读者应该都知道，无论是加大购买量，还是扩大购买范围，都很难集齐全套水浒英雄。
这其实就是一个P/NP问题——是否有一种方法，让集卡的过程轻而易举？
所以，GPT-4是怎样得出P≠NP的？让我们往下看。
97轮对话，给出P≠NP结论
在这项研究中，研究者GPT-4学会了一种「苏格拉底式推理」。
他们引入了五个不同的角色（比如精通概率论的数学家），作为协助证明者，根据自己擅长证明不同的部分。
GPT-4用这种方法，开发了一种推理路径，得出了和北航Ke Xu、北工商Guangyan Zhou（论文三作和四作）最近提出结果一致的结论！
论文地址：https://arxiv.org/pdf/2302.09512.pdf
在最初的14轮对话中，GPT-4被引导设计出了初步的证明模式。
GPT-4被问的第一个问题是：「你能从哲学角度而不是计算机理论角度找到P!=NP问题背后的根本问题吗？」
在这个提示中，技巧在于鼓励模型创造性回答，避免进行检索。比如，「如何证明 P!=NP」这样的提示可能会引导大模型进行检索。
用上「苏格拉底式推理」中的转换模式后，就可以生成更具创新性的回答。
对于这个问题，GPT-4是这么回答的——
P!=NP问题背后的基本哲学问题，可以看作是创造力、直觉和洞察力（通常与NP问题相关）与系统化、算法和确定性方法（与P问题相关）之间的矛盾。
如果P=NP，那就意味着宇宙有一种基本的简单性，表面上看似复杂的问题都有高效、优雅的解决方案。
看来，GPT-4对P!=NP理解得很透彻，在此基础上，研究者开始提问了——
「 是否所有表面上看似复杂的问题都有高效、优雅的解决方案？如果不是，可以用什么方法来证明？」
GPT-4回答说，并非所有表面看来复杂的问题都有高效、优雅的解决方案，这可以归因于多种因素，比如所涉及变量的数量、变量之间关系的性质，或问题本身的内在难度。
然后，它提出了六种方法，其中一种是「矛盾证明」，即要证明一个问题没有高效、优雅的解决方案，可以假设存在这样的解决方案，然后证明这一假设会导致矛盾，这样就可以有力地证明某些解法不可能存在。
可以看到，GPT-4在回答问题过程中，真的像人类一样拥有思辨能力。
紧接着，研究人员趁热打铁，继续问道，「我们想用矛盾证明P!=NP，请列出几种可能的思路。」
这次GPT-4依然给出了六个答案，不过并不严谨。
要通过矛盾证明，必须找到一个无法在多项式时间内解决的NP完全（NP-complete）问题。
不过，这个回答可以启发GPT-4在以后的对话中思考NP完全问题。
在第四轮提问中，GPT-4的回答中出现了诸多亮点。
「该怎样构建这些问题呢？」
比如它回答说：我们可以从众所周知的NP完全问题入手，例如旅行商问题 （TSP）、布尔可满足性问题（SAT）或分团问题（Clique）。
随后的提问中，GPT-4被引导着给出了越来越多智慧的回答，也让研究开始一步步深入问题中心。
就这样，经过14轮连续对话，研究人员让GPT-4对3-13步的历史内容，梳理出一个证明思路。
对此，GPT-4的总结中，突出显示的两个部分是研究后续证明的2个关键点。
第4点建立了一个基本的直觉，即一旦证明了极难CSP的存在，就可以使用「矛盾证明」来证明这些问题无法在多项式时间内求解。
而第6点恰好成为后续证明工作的通用模式。
从下一轮开始，研究人员便遵循这一初步方案，严格地进行证明。
然后，研究者按照草稿，在随后的83轮对话中进行了严格的推理。
而这97轮对话，可以说构建出了一个极难的NP完全问题，其中一些实例在时间复杂度低于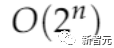
（即穷举搜索）的情况下是不可解的，也就是说，证明结论为P≠NP。
是的，如果你能严格证明存在一种特定类型的NP完全问题，当变量数趋于无穷大时，无法在多项式时间内求解这类问题，就可以认为，证明了P!=NP。
在Ke Xu和Guangyan Zhou的论文中，他们构建了CSP和SAT的极难示例，证明了这些示例在没有穷举法的情况下无法求解。
而GPT-4，也得出了一致的结论。
是的，如果我们能够证明不存在一种算法能够以低于
的时间复杂度解决某些SAT实例，那么当变量数量趋于无穷大时，它确实可以为某些无法在多项式时间内解决的NP完全问题的存在提供强有力的证据。
这项研究再次证明，GPT-4有充分的潜力与人类合作，共同探索极其复杂的专家级难题。
LLM不仅能掌握基本知识，还可以在广泛的解空间中发现新的见解。这也预示着科学LLM的范式下，科学发现的无限前景。
苏格拉底式推理
那么，GPT-4展现出如此强大，思维推理能力，背后的极致究竟是什么呢？
古希腊哲学家苏格拉曾说过，「我不能教会别人任何事，我只能让他们思考」。
这次，研究人员恰巧就从中汲取了灵感，提出一种通用问题的解决框架——苏格拉底式推理（Socratic Reasoning）。
简单讲，苏格拉底方法就是让我们「一步一步思考」，提出一系列问题激发批判性思维。
这对于大模型来说，如果能够进行批判性思考，就可以针对复杂问题提出高效的解决方案。
对此，研究团队指出这一框架旨在推动LLM解决高度复杂任务，协调各种子问题，并引导其搭建高层次推理途径。
「苏格拉底式推理」是在人类与LLM之间的一系列对话回合中进行的，是与LLM一起解决复杂挑战的递归机制。
如下图所示，「苏格拉底式推理」有5种强大的提示模式：演绎、转换、分解、验证、整合。
通过发掘新的见解和观点，将复杂问题分解为子问题或步骤，并通过质疑回答进行自我完善。
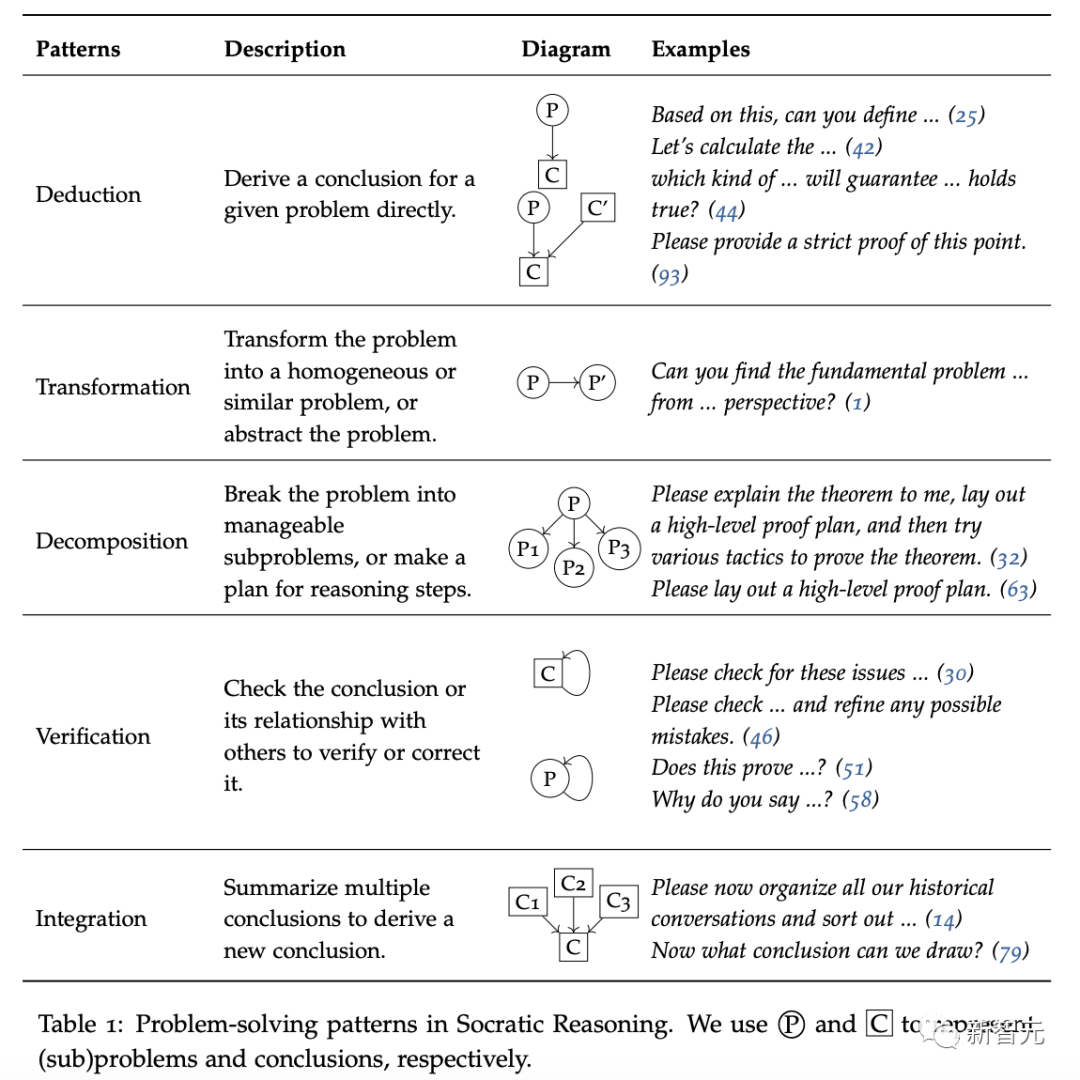
「苏格拉底式推理」中的问题解决模式（用
和
分别表示（子）问题和结论
一般来说，在处理可以直接从推理中得出结论的问题时，会采用「演绎模式」（如 「让我们一步步思考」）来指导LLM直接得出结论。
对于更复杂的问题，首先要求LLM将问题转化为新问题，或分解为若干子问题。然后，通过递归方法，直到找到「原子问题」。
P vs. NP问题对话转换示例
在生成新问题或得出新结论时，通过「验证模式」，利用LLM自我批判能力进行验证和完善。
最后，「整合模式」要求 LLM 基于子问题的结果合成结论。
整个流程，研究人员鼓励LLM通过一系列对话，递归地继续上述过程，直至解决目标问题。
这篇论文，研究人员揭示了大模型能够在解决科学问题中大有可为，能够在得出复杂问题结论中细化攻坚的策略。
通过97论文对话引导，GPT-4展现出超人能力，完成了千禧数学难题全推理过程。
作者介绍
Qingxiu Dong，北京大学计算语言学研究所博士生。
Li Dong，微软亚洲研究院首席研究员。
此前，他曾于2010年至2015年，在北航软件开发环境国家重点实验室跟随Ke Xu从事研究工作。
Ke Xu，北京航空航天大学计算机科学教授。
此前，他在北京航空航天大学获得了学士、硕士和博士学位。研究兴趣包括算法与复杂性、数据挖掘和网络。
