本文经自动驾驶之心公众号授权转载,转载请联系出处。
假如我们有无限的资源,比如有无穷多的数据,无穷大的算力,无穷大的模型,完美的优化算法与泛化表现,请问由此得到的预训练模型是否可以用来解决一切问题?
这是一个大家都非常关心的问题,但已有的机器学习理论却无法回答。它与表达能力理论无关,因为模型无穷大,表达能力自然也无穷大。它与优化、泛化理论也无关,因为我们假设算法的优化、泛化表现完美。换句话说,之前理论研究的问题在这里不存在了!
今天,我给大家介绍一下我在ICML'2023发表的论文On the Power of Foundation Models,从范畴论的角度给出一个答案。
范畴论是什么?
倘若不是数学专业的同学,对范畴论可能比较陌生。范畴论被称为是数学的数学,为现代数学提供了一套基础语言。现代几乎所有的数学领域都是用范畴论的语言描述的,例如代数拓扑、代数几何、代数图论等等。范畴论是一门研究结构与关系的学问,它可以看作是集合论的一种自然延伸:在集合论中,一个集合包含了若干个不同的元素;在范畴论中,我们不仅记录了元素,还记录了元素与元素之间的关系。
Martin Kuppe曾经画了一幅数学地图,把范畴论放到了地图的顶端,照耀着数学各个领域:
关于范畴论的介绍网上有很多,我们这里简单讲几个基本概念:

监督学习的范畴论视角

过去十多年,人们围绕着监督学习框架进行了大量的研究,得到了很多优美的结论。但是,这一框架也限制了人们对AI算法的认识,让理解预训练大模型变得极为困难。例如,已有的泛化理论很难用来解释模型的跨模态学习能力。

我们能不能通过采样函子的输入输出数据,学到这个函子?
注意到,在这个过程中我们没有考虑两个范畴 X,Y 内部的结构。实际上,监督学习没有对范畴内部的结构有任何假设,所以可以认为在两个范畴内部,任何两个对象之间都没有关系。因此,我们完全可以把 X 和 Y 看作是两个集合。这个时候,泛化理论著名的no free lunch定理告诉我们,假如没有额外假设,那么学好从 X 到 Y 的函子这件事情是不可能的(除非有海量样本)。

乍看之下,这个新视角毫无用处。给范畴加约束也好,给函子加约束也好,似乎没什么本质区别。实际上,新视角更像是传统框架的阉割版本:它甚至没有提及监督学习中极为重要的损失函数的概念,也就无法用于分析训练算法的收敛或泛化性质。那么我们应该如何理解这个新视角呢?
我想,范畴论提供了一种鸟瞰视角。它本身不会也不应该替代原有的更具体的监督学习框架,或者用来产生更好的监督学习算法。相反,监督学习框架是它的“子模块”,是解决具体问题时可以采用的工具。因此,范畴论不会在乎损失函数或者优化过程——这些更像是算法的实现细节。它更关注范畴与函子的结构,并且尝试理解某个函子是否可学习。这些问题在传统监督学习框架中极为困难,但是在范畴视角下变得简单。
自监督学习的范畴论视角
预训练任务与范畴

下面我们先明确在预训练任务下范畴的定义。实际上,倘若我们没有设计任何预训练任务,那么范畴中的对象之间就没有关系;但是设计了预训练任务之后,我们就将人类的先验知识以任务的方式,给范畴注入了结构。而这些结构就成为了大模型拥有的知识。
具体来说:

换句话说,当我们在一个数据集上定义了预训练任务之后,我们就定义了一个包含对应关系结构的范畴。预训练任务的学习目标,就是让模型把这个范畴学好。具体来说,我们看一下理想模型的概念。
理想模型

在这里,“数据无关”意味着 是在看到数据之前就预先定义的;但下标 f则表示可以通过黑盒调用的方式使用 f 和 这两个函数。换句话说, 是一个“简单”的函数,但可以借助模型 f 的能力来表示更复杂的关系。这一点可能不太好理解,我们用压缩算法来打个比方。压缩算法本身可能是数据相关的,比如它可能是针对数据分布进行了特殊优化。然而,作为一个数据无关的函数 ,它无法访问数据分布,但可以调用压缩算法来解压数据,因为“调用压缩算法”这一操作是数据无关的。
针对不同的预训练任务,我们可以定义不同的 :

因此,我们可以这么说:预训练学习的过程,就是在寻找理想模型 f 的过程。
可是,即使 是确定的,根据定义,理想模型也并不唯一。理论上说,模型 f 可能具有超级智能,即使在不学习 C 中数据的前提下也能做任何事情。在这种情况下,我们无法对 f 的能力给出有意义的论断。因此,我们应该看看问题的另一面:
给定由预训练任务定义的范畴 C ,对于任何一个理想的 f ,它能解决哪些任务?
这是我们在本文一开始就想回答的核心问题。我们先介绍一个重要概念。
米田嵌入
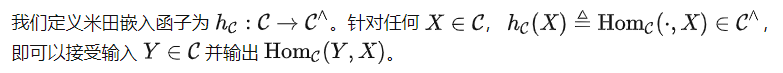

很容易证明, 是能力最弱的理想模型,因为给定其他理想模型 f , 中的所有关系也包含在 f 中。同时,它也是没有其他额外假设前提之下,预训练模型学习的最终目标。因此,为了回答我们的核心问题,我们下面专门考虑 。
提示调优(Prompt tuning): 见多才能识广

能否解决某个任务 T ?要回答这个问题,我们先介绍范畴论中最重要的一个定理。
米田引理

即, 可以用这两种表征计算出 T(X) 。然而,注意到任务提示 P 必须通过 而非 发送,这意味着我们会得到 (P) 而非 T 作为 的输入。这引出了范畴论中另一个重要的定义。
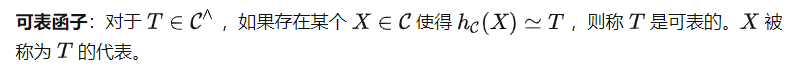
基于这个定义,我们可以得到如下定理(证明略去)。
定理1与推论

值得一提的是,有些提示调优算法的提示不一定是范畴 C 中的对象,可能是特征空间中的表征。这种方法有可能支持比可表任务更复杂的任务,但增强效果取决于特征空间的表达能力。下面我们提供定理1的一个简单推论。
推论1. 对于预测图像旋转角度的预训练任务[4],提示调优不能解决分割或分类等复杂的下游任务。
证明:预测图像旋转角度的预训练任务会将给定图像旋转四个不同的角度:0°, 90°, 180°, 和 270°,并让模型进行预测。因此,这个预训练任务定义的范畴将每个对象都放入一个包含4个元素的群中。显然,像分割或分类这样的任务不能由这样简单的对象表出。
推论1有点反直觉,因为原论文提到[4],使用该方法得到的模型可以部分解决分类或分割等下游任务。然而,在我们的定义中,解决任务意味着模型应该为每个输入生成正确的输出,因此部分正确并不被视为成功。这也与我们文章开头提到的问题相符:在无限资源的支持下,预测图像旋转角度的预训练任务能否用于解决复杂的下游任务?推论1给出了否定的答案。
微调(Fine tuning): 表征不丢信息
提示调优的能力有限,那么微调算法呢?基于米田函子扩展定理(参见 [5]中的命题2.7.1),我们可以得到如下定理。
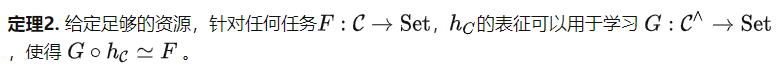
定理2考虑的下游任务是基于 C 的结构,而不是数据集中的数据内容。因此,之前提到的预测旋转图片角度的预训练任务定义的范畴仍然具有非常简单的群结构。但是根据定理2,我们可以用它解决更多样化的任务。例如,我们可以将所有对象映射到同一个输出,这是无法通过提示调优来实现的。定理2明确了预训练任务的重要性,因为更好的预训练任务将创建更强大的范畴 C ,从而进一步提高了模型的微调潜力。
对于定理2有两个常见的误解。首先,即使范畴 C 包含了大量信息,定理2只提供了一个粗糙的上界,说 记录了 C 中所有的信息,有潜力解决任何任务,而并没有说任何微调算法都可以达到这个目的。其次,定理2乍看像是过参数化理论。然而,它们分析的是自监督学习的不同步骤。过参数化分析的是预训练步骤,说的是在某些假设下,只要模型足够大且学习率足够小,对于预训练任务,优化和泛化误差将非常小。而定理2分析的则是预训练后的微调步骤,说该步骤有很大潜力。
讨论与总结
监督学习与自监督学习。从机器学习的角度来看,自监督学习仍然是一种监督学习,只是获取标签的方式更巧妙一些而已。但是从范畴论的角度来看,自监督学习定义了范畴内部的结构,而监督学习定义了范畴之间的关系。因此,它们处于人工智能地图的不同板块,在做完全不一样的事情。

适用场景。由于本文开头考虑了无限资源的假设,导致很多朋友可能会认为,这些理论只有在虚空之中才会真正成立。其实并非如此。在我们真正的推导过程中,我们只是考虑了理想模型与 这一预定义的函数。实际上,只要 确定了之后,任何一个预训练模型 f (哪怕是在随机初始化阶段)都可以针对输入XC 计算出 f(X) ,从而使用 计算出两个对象的关系。换句话说,只要当 确定之后,每个预训练模型都对应于一个范畴,而预训练的目标不过是将这个范畴不断与由预训练任务定义的范畴对齐而已。因此,我们的理论针对每一个预训练模型都成立。
核心公式。很多人说,如果AI真有一套理论支撑,那么它背后应该有一个或者几个简洁优美的公式。我想,如果需要用一个范畴论的公式来描绘大模型能力的话,它应该就是我们之前提到的:
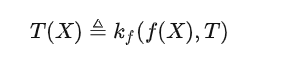
对于大模型比较熟悉的朋友,在深入理解这个公式的含义之后,可能会觉得这个式子在说废话,不过是把现在大模型的工作模式用比较复杂的数学式子写出来了而已。
但事实并非如此。现代科学基于数学,现代数学基于范畴论,而范畴论中最重要的定理就是米田引理。我写的这个式子将米田引理的同构式拆开变成了不对称的版本,却正好和大模型的打开方式完全一致。
我认为这一定不是巧合。如果范畴论可以照耀现代数学的各个分支,它也一定可以照亮通用人工智能的前进之路。
本文灵感源于与北京智源人工智能研究院千方团队的长期紧密合作。

原文链接:https://mp.weixin.qq.com/s/bKf3JADjAveeJDjFzcDbkw