
大家好,我是前端西瓜哥。
我开发的图形编辑器,原本选中图形是基于选区是否完全包含对应图形来判断其是否被选中,使用的是矩形包含判断。
编辑器 github 地址:
https://github.com/F-star/suika
线上体验:
https://blog.fstars.wang/app/suika/
但用着用着,我发现包含可能并不是一个好策略。
我想要选中一个大矩形,就比较费劲,要画一个比它还大的选区,可能还会把其他的矩形不小心放进去(那你别用选区,直接点选啊)。
不管怎样,我选择同时提供 “包含(contain)” 和 "相交(intersect)" 两种模式,默认使用相交策略。
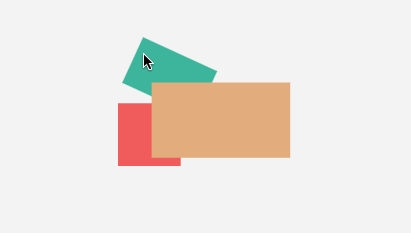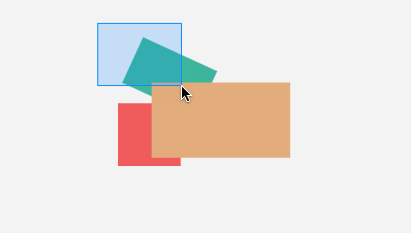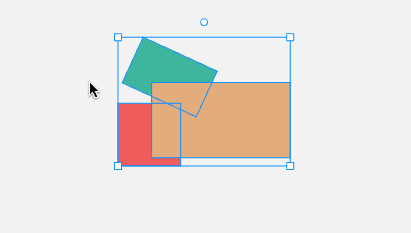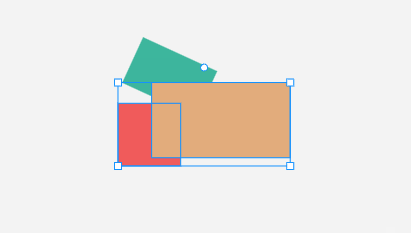
包含选择
包含策略很简单,遍历图形,对比 selection 选区矩形和图形的包围盒,判断是否为前者包含后者的关系。
如果是,就放到选中图形集合中。
相比相交的实现,算法不复杂。
// 矩形 1 是否包含矩形 2
function isRectContain(rect1: IRect, rect2: IRect) {
return (
rect1.x <= rect2.x &&
rect1.y <= rect2.y &&
rect1.x + rect1.width >= rect2.x + rect2.width &&
rect1.y + rect1.height >= rect2.y + rect2.height
);
}
// 使用
for (const el of elements) {
// getBBox 拿到的是 AABB 包围盒
if(isRectContain(selection, el.getBBox())) {
selectSet.add(el);
}
}相交选择
相交(也叫碰撞)的实现类似。
// 两矩形是否相交
function isRectIntersect(rect1: IRect, rect2: IRect) {
return (
rect1.x <= rect2.x + rect2.width &&
rect1.x + rect1.width >= rect2.x &&
rect1.y <= rect2.y + rect2.height &&
rect1.y + rect1.height >= rect2.y
);
}
// 使用
for (const el of elements) {
// getBBox 拿到的是 AABB 包围盒
if(isRectIntersect(selection, el.getBBox())) {
selectSet.add(el);
}
}效果:
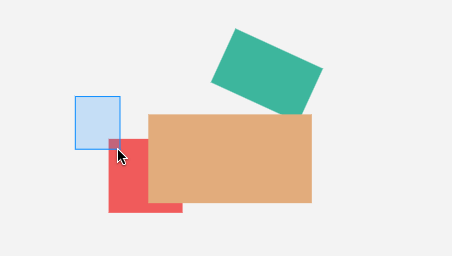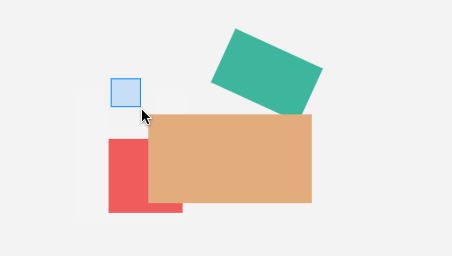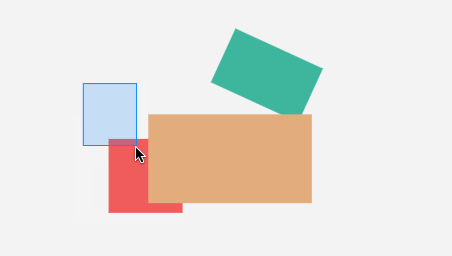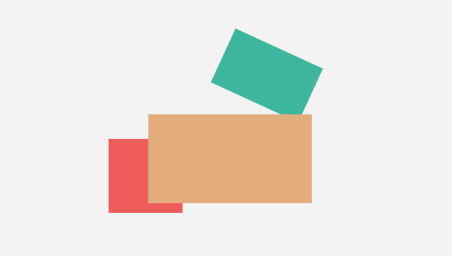
看起来不错,但它这个相交检测,很 “粗糙”。
因为上面实现,只做了大的 AABB 包围盒的相交检测,没有做小的 OBB 包围盒的相交检测。
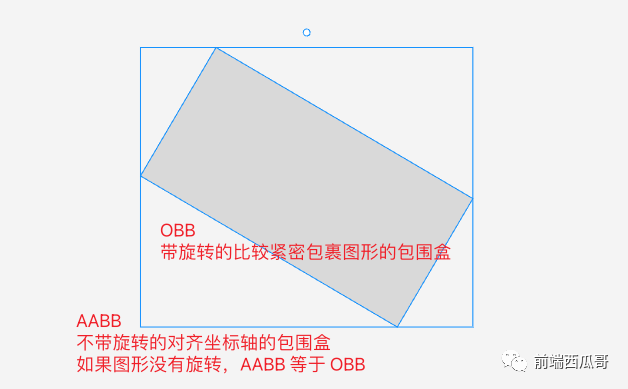
对于发生旋转的图形,selection 如果和包裹图形的空白区域相交了,图形也被选中。

这种事情,不要啊。
OBB 相交检测
我们来实现更精准的 OBB 的相交检测。
为此西瓜哥我调研(其实是瞎想)了几个方案,并研究了算法实现。
方案 1:线段相交判断
直接一点,判断 selection 的边和图形的边是否有相交的。
核心算法实现为:
type Point = [number, number];
function crossProduct(p1: Point, p2: Point, p3: Point): number {
const x1 = p2[0] - p1[0];
const y1 = p2[1] - p1[1];
const x2 = p3[0] - p1[0];
const y2 = p3[1] - p1[1];
return x1 * y2 - x2 * y1;
}
function isSegmentIntersect(
seg1: [Point, Point],
seg2: [Point, Point],
): boolean {
const [a, b] = seg1;
const [c, d] = seg2;
const d1 = crossProduct(a, b, c);
const d2 = crossProduct(a, b, d);
const d3 = crossProduct(c, d, a);
const d4 = crossProduct(c, d, b);
// 突然发现这里可以做一个短路计算优化
return d1 * d2 < 0 && d3 * d4 < 0;
}光是比较 1 对线段,就要进行如此多的计算。而我们要对比 4 * 4,共 16 组(当然这是最坏情况)。
感觉 8 太行,最后没选择该方案。
(理论上应该做性能测试对比各种实现的,还要考虑用户使用选区的场景,是否会经常出现特定算法的最坏时间复杂度的情形,有空再做吧)
方案2:分离轴定理算法
这个算法挺有意思。
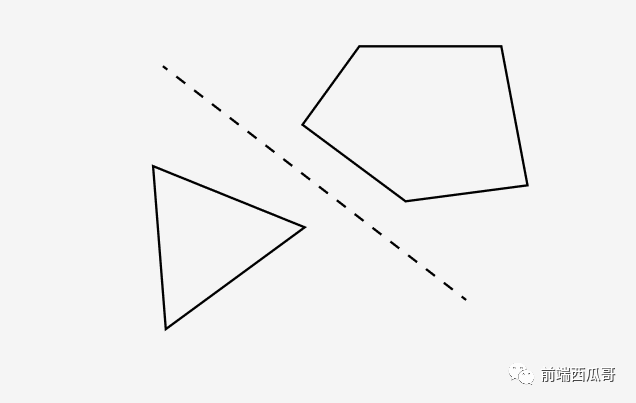
分离轴(Separating Axis Theorem,简称SAT),它的思想是:
如果能找到一条直线将两个图形分开,那说明这两个图形不相交。
如图:
具体做法是做投影。(通过降维,将大问题拆分成小问题)
我们会对两个凸多边形做投影,投影到的线称为 “分离轴”。
分离轴基本选择的是两个图形的每条边对应的法向量。当发现投影产生的两条线段没有相交,那找到了那条那条分割两图形的直线,证明两个凸多边形不相交。
否则继续,如果都没找到,说明相交。
下图是以一个图形的蓝边的法向量作为分离轴,进行投影的示意图。
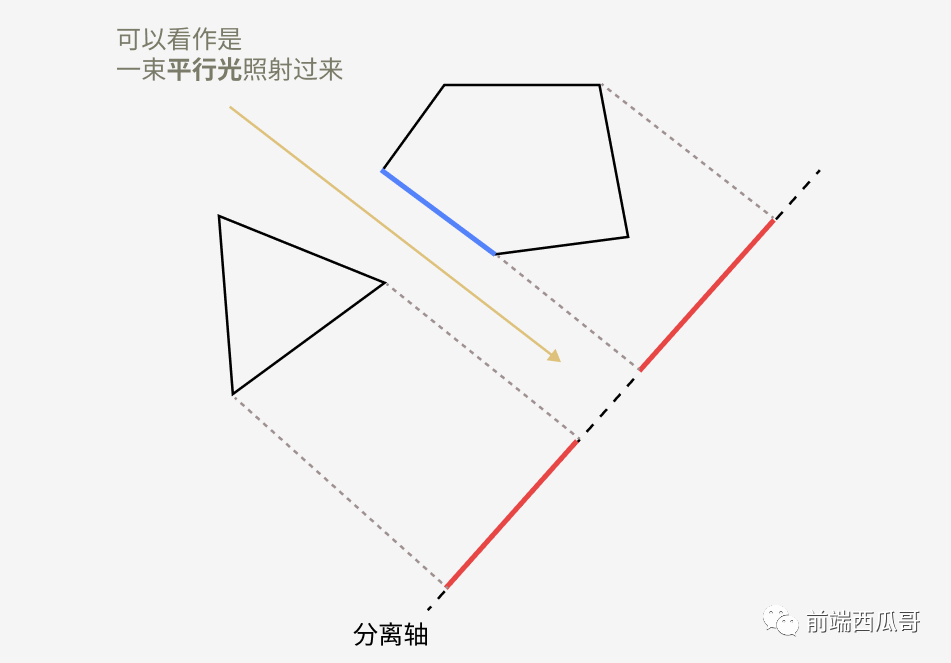
求投影会用到向量点乘的运算。
因为不是本文重点,具体实现细节就不讲解了,可以考虑以后专门写一篇文章。
矩形碰撞,特殊的分离轴定理碰撞
不知道你发现没有,从分离轴线的角度去看,两个没有旋转矩形的相交判断,其实是一个特例。
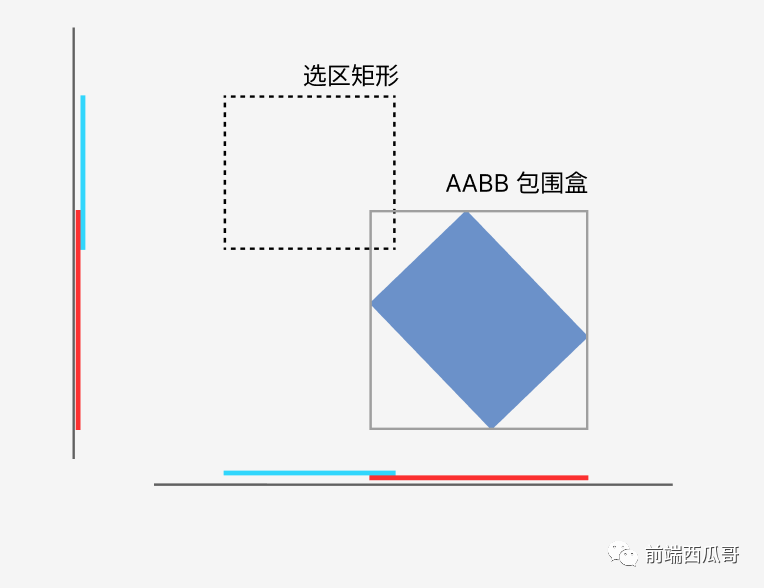
我们在判断选区矩形和图形的 AABB 包围盒是否相交时,其实就已经完成了 基于选区矩形对应的所有分离轴 的投影上是否相交的比较。
接下来我们只要再对图形的边对应的分离轴线投影,去对比就好了。
怎么做呢?
我们 “旋转回来”,将图形掰正,选区矩形产生了旋转角度,计算选区矩形的 AABB 包围盒,再进行矩形对比就好了。
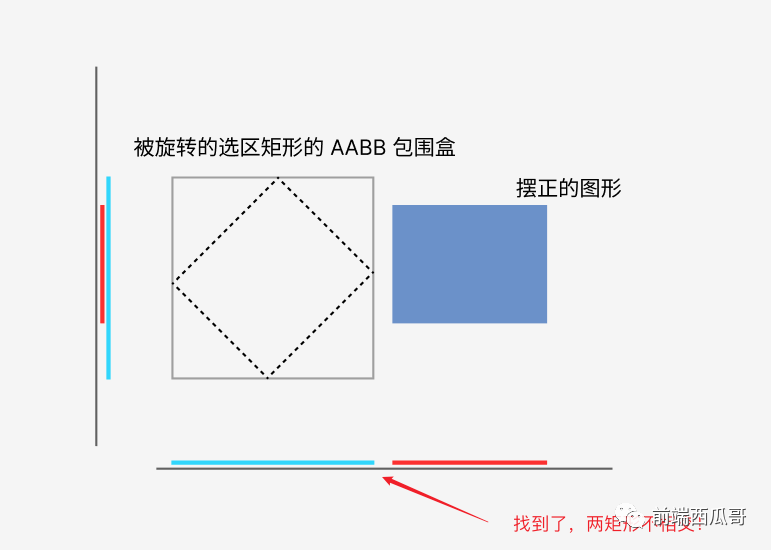
这样,图形的分离轴的投影也对比完了,所有的分离轴都对比了,就能判断出选区和图形的 OBB 包围盒是否碰撞了。
甚至都不用向量点乘。
OBB 相交判断代码实现
下面给出代码实现。
// 使用相交策略,遍历图形是否和选区矩形相交。
for (const el of elements) {
let isSelected = false; // 是否被选中到
// 首先做 AABB 碰撞检测
// 绝大多数场景下,只有少数图形和选区有相交
if (!isRectIntersect(selection, el.getBBox())) {
// 其实这里用 break; 在意图上更明显
isSelected = false;
} else {
// 如果旋转角度为 90 的倍数,
// 则 OBB 等价于 AABB,前面已经判断了,没必要继续算了
if (el.rotation % HALF_PI == 0) {
isSelected = true;
} else {
// OBB 碰撞检测
// 使用分离轴定理的特殊写法
const { x: cx, y: cy } = el.getCenter();
const r = -el.rotation;
const s1 = transformRotate(selection.x, selection.y, r, cx, cy);
// 下面一大段代码都是求选区旋转后的 AABB
const s2 = transformRotate(
selection.x + selection.width,
selection.y + selection.height,
r,
cx,
cy,
);
const s3 = transformRotate(
selection.x + selection.width,
selection.y,
r,
cx,
cy,
);
const s4 = transformRotate(
selection.x,
selection.y + selection.height,
r,
cx,
cy,
);
const rotatedSelectionX = Math.min(s1.x, s2.x, s3.x, s4.x);
const rotatedSelectionY = Math.min(s1.y, s2.y, s3.y, s4.y);
const rotatedSelectionWidth =
Math.max(s1.x, s2.x, s3.x, s4.x) - rotatedSelectionX;
const rotatedSelectionHeight =
Math.max(s1.y, s2.y, s3.y, s4.y) - rotatedSelectionY;
// 这个就是选区矩形旋转后的 AABB 包围盒
const rotatedSelection = {
x: rotatedSelectionX,
y: rotatedSelectionY,
width: rotatedSelectionWidth,
height: rotatedSelectionHeight,
};
// 对比它们(注意图形不要再用 AABB 了)
isSelected = isRectIntersect(rotatedSelection, {
x: el.x,
y: el.y,
width: el.width,
height: el.height,
});
}
}
// 更新选中图形集合
if (isSelected) {
selectSet.add(el);
}
}看看效果,很完美。

结尾
矩形相交是分离轴定理相交算法的特殊情况。











































