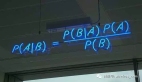近来,大规模神经网络彻底改变了生成式模型,使模型具有前所未有的捕捉许多变量之间复杂关系的能力,例如建立高分辨率图像中所有像素的联合模型。
大多数神经网络(包括自回归模型、基于流的模型、深度 VAE 和扩散模型)表达能力的关键在于,它们编码的联合分布被分解为一系列步骤,从而避免了「维数灾难(curse of dimensionality)」。也就是说,它们将难题分解成多个简单问题来解决。
自回归网络目前是语言建模领域的 SOTA 方法,并且通常在自然排序的离散数据上表现良好。然而,事实证明自回归网络在图像生成等领域效果较差,因为这些领域的数据是连续的,并且变量之间不存在自然顺序。自回归模型还有一个缺点是,生成样本需要与数据中变量一样多的网络更新。扩散模型是一种应用于图像生成的有效替代框架,但传输过程会变得更加复杂。
然而,当数据是离散的,扩散模型的性能仍不及自回归模型。最近,机器学习领域知名研究者、神经图灵机(NTM)提出者和可微神经计算机的创造者之一 Alex Graves 以第一作者的身份发表了一篇新论文,提出了一种新型生成模型 —— 贝叶斯流网络(Bayesian Flow Networks,BFN)。与扩散模型不同的是,BFN 对数据分布的参数进行操作,而不是对数据本身的噪声版本进行操作。这确保了生成过程是完全连续且可微的,即使数据是离散的。

论文地址:https://arxiv.org/abs/2308.07037

论文一作 Alex Graves,他是图灵奖得主 Geoffrey Hinton 的学生。
BFN 方法会根据噪声数据样本使用贝叶斯推断修改一组独立分布的参数,然后将其作为输入传递给神经网络,该神经网络会输出一个相互依赖的分布,然后从简单的先验开始并迭代更新上述两个分布,产生一种类似于扩散模型逆过程的生成过程,但 BFN 在概念上更简单,因为不需要前向过程。
BFN 的整体概览如下图 1 所示。在每一步中,消息发送者(Sender)Alice 都会向消息接收者(Receiver)Bob 发送一条消息,包含关于数据的一些信息。
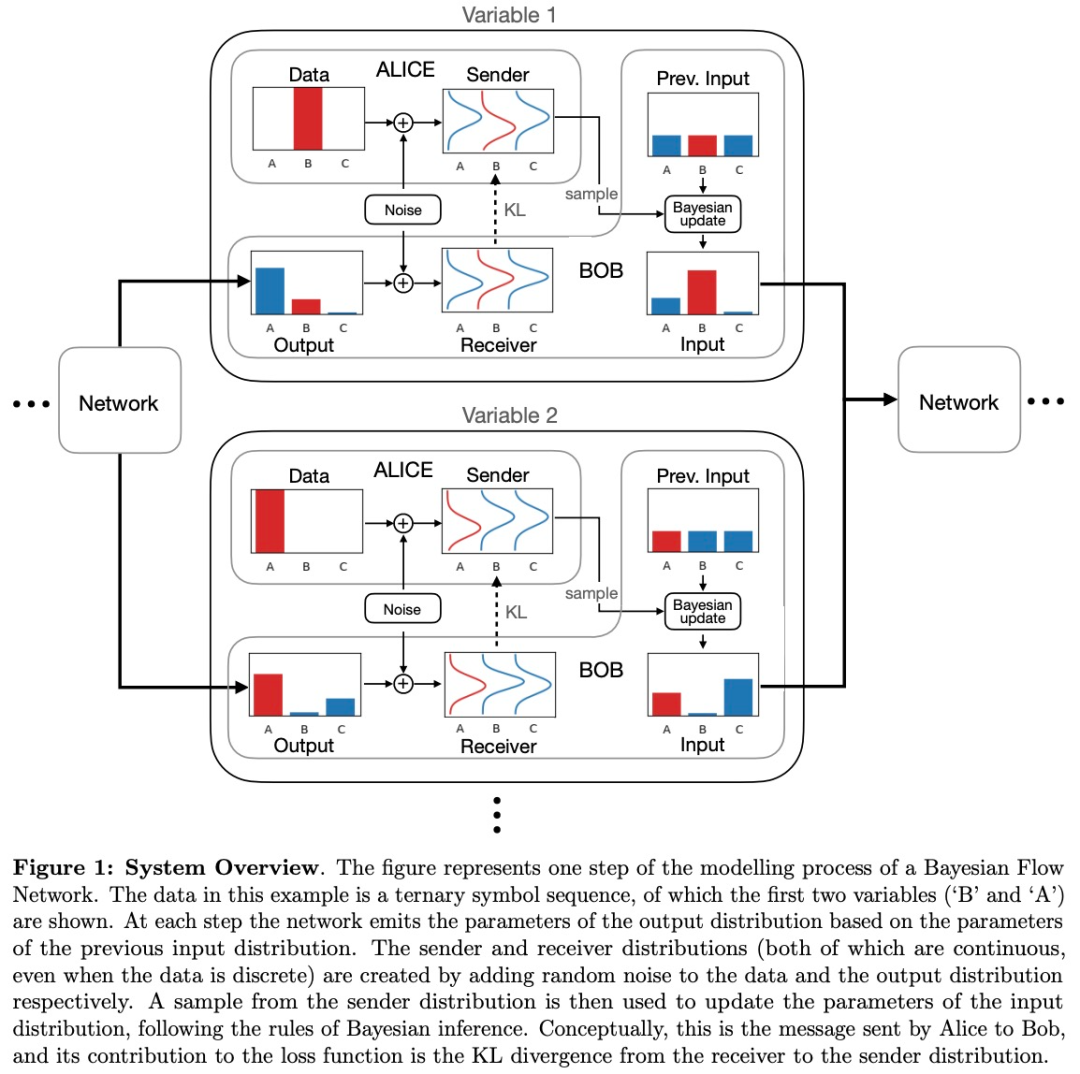
其中,Bob 会尝试猜测消息是什么:他猜测得越好,传输消息所需的比特数就越少。收到消息后,Bob 使用刚刚获得的信息来改进对下一条消息的猜测。
重复该过程,每一步的预测都会得到改进。传输成本之和是完整文本序列的负对数概率,通过最大似然训练进行损失函数最小化。这也是 Alice 使用算术编码将片段传输给 Bob 所需的最小位数。因此,用最大似然拟合自回归模型与训练数据压缩之间存在直接的对应关系。
上述传输过程定义了一个 n 步损失函数,通过将 n 扩展到∞,就能推广到连续时间。连续时间损失函数在数学上比离散时间损失函数更简单、易于计算。经过连续时间损失训练的 BFN 可以在推断和采样期间运行任意数量的离散步骤,并且性能随着步骤数量的增加而提升。
总的来说,BFN 结合了贝叶斯推断和深度学习的优势,前者为单个变量提供了一种极佳的数学方法,后者则擅长整合多个相关变量的信息。
LSTM 提出者和奠基者 Sepp Hochreiter 表示:「贝叶斯流网络 (BFN) 作为扩散模型的替代者,它更新的两个分布过程可看作是一个生成过程,就像没有前向传递的扩散模型一样。实验显示,在 text8 字符级语言建模上优于离散扩散。」
论文作者之一 Rupesh Kumar Srivastava 表示,「这项研究使得我们可以通过选择合适的分布,轻松地将 BFN 框架适应于连续和离散数据,并且在 MNIST、CIFAR-10 和 text8 任务上得到了很好的结果。」
贝叶斯流网络
接下来我们介绍一下贝叶斯流网络(Bayesian Flow Networks,BFN)的基本数学形式。本节都是公式推导,大家可以参考原论文了解更详细的信息。
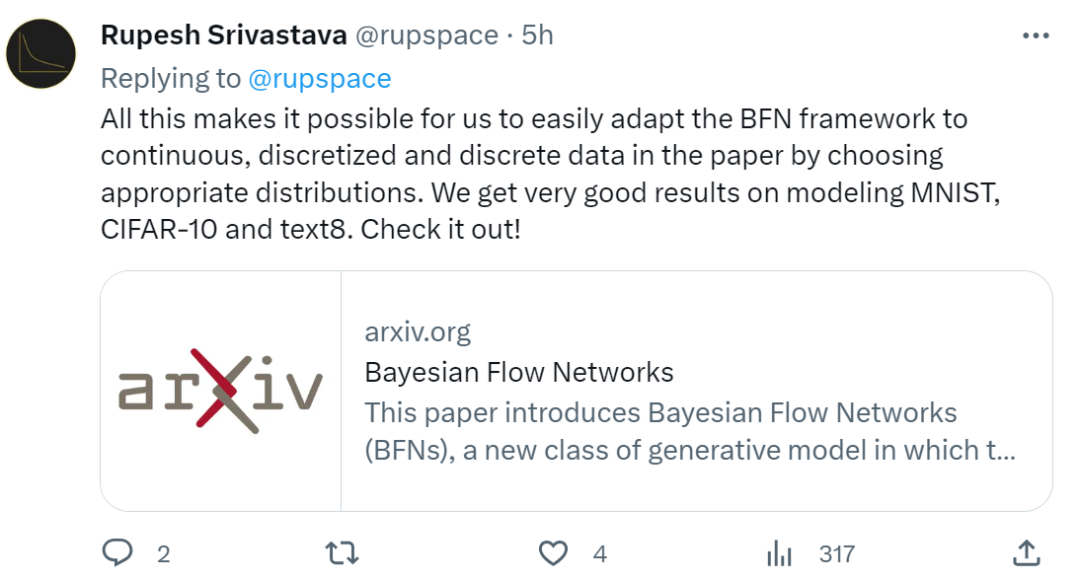
输入分布和 Sender 分布:给定 D 维数据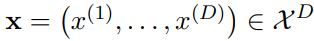 ,
,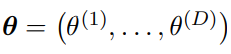 为因式输入分布
为因式输入分布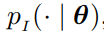 的参数,则输入分布公式如下:
的参数,则输入分布公式如下:
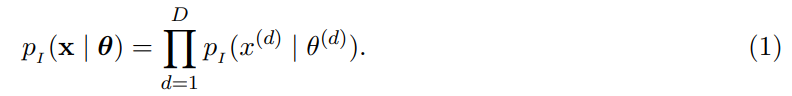
经过一系列变换后,得到 Sender 分布公式:
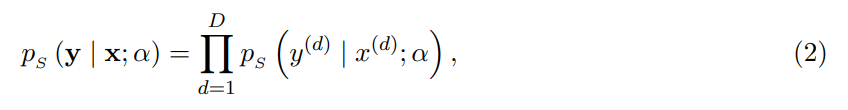
输出分布数据传输过程中,输入参数 θ 与过程时间 t 一起作为输入传递给神经网络 Ψ,然后网络输出一个向量,得到输出分布:
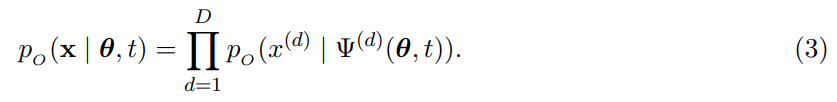
与输入分布不同,输出分布可以利用上下文信息,例如图像中的周围像素或文本中的相关单词。
Receiver 分布给定 Sender 分布和输出分布, Receiver 分布可以表述为:
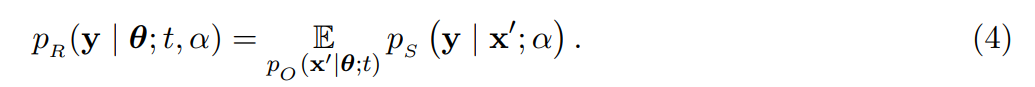
由上式可得,Receiver 分布有两个不确定来源,即 Sender 分布和输出分布。
贝叶斯更新
对于给定的参数 θ,参数更新的方式如下所示,其中 y 为 Sender 样本, α 为准确率:

得到贝叶斯更新分布:
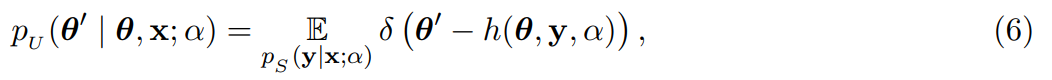
本文认为,从某种意义上讲,准确率 α 是可以相加的,从而得到总的贝叶斯更新分布公式:
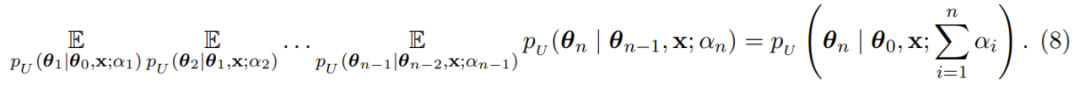
通过执行无限多的传输步骤,贝叶斯更新过程可以推广到连续时间。假设 t ∈ [0, 1] 为处理时间,α(t) > 0 为时间 t 的准确率,得到准确率时间表:

贝叶斯流分布
给定先验参数 θ_0、贝叶斯更新分布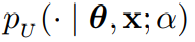 以及准确率时间表 β(t), 贝叶斯流分布可以表示为
以及准确率时间表 β(t), 贝叶斯流分布可以表示为
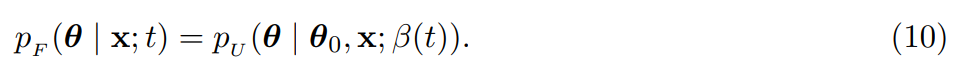
损失函数
损失函数定义为如下方式:

其中,
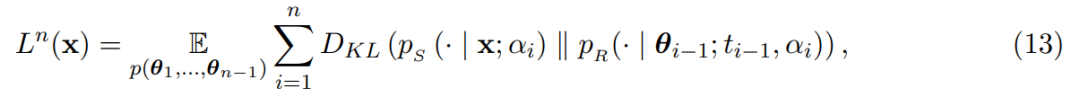
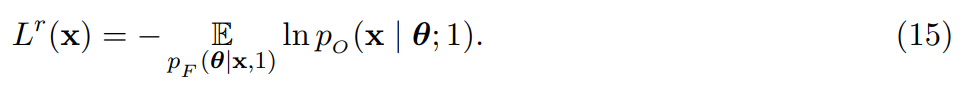
L (x) 可以推导为变分自编码器(VAE)的损失函数,经过一系列变化,损失函数表述为:
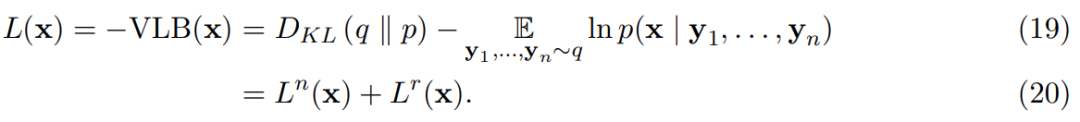
根据损失函数(16),该研究又推导出了离散损失:
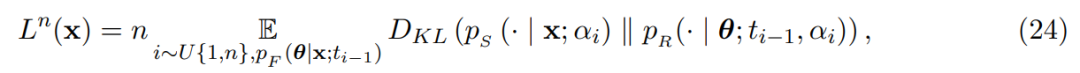
以及连续时间损失:
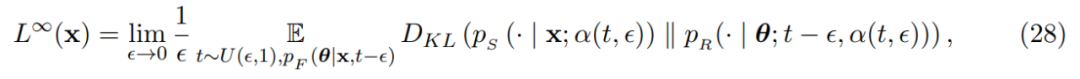
实验
该研究在以下生成基准上评估了 BFN 网络,包括 CIFAR-10(32×32 8 位彩色图像)、动态二值化 MNIST(28×28 手写数字的二值化图像)以及 text8(长度 256 个字符序列,大小为 27 个字母)。
动态二值化 MNIST
从表 1 可以看出,BFN 在没有数据增强的情况下达到该任务最好的性能。
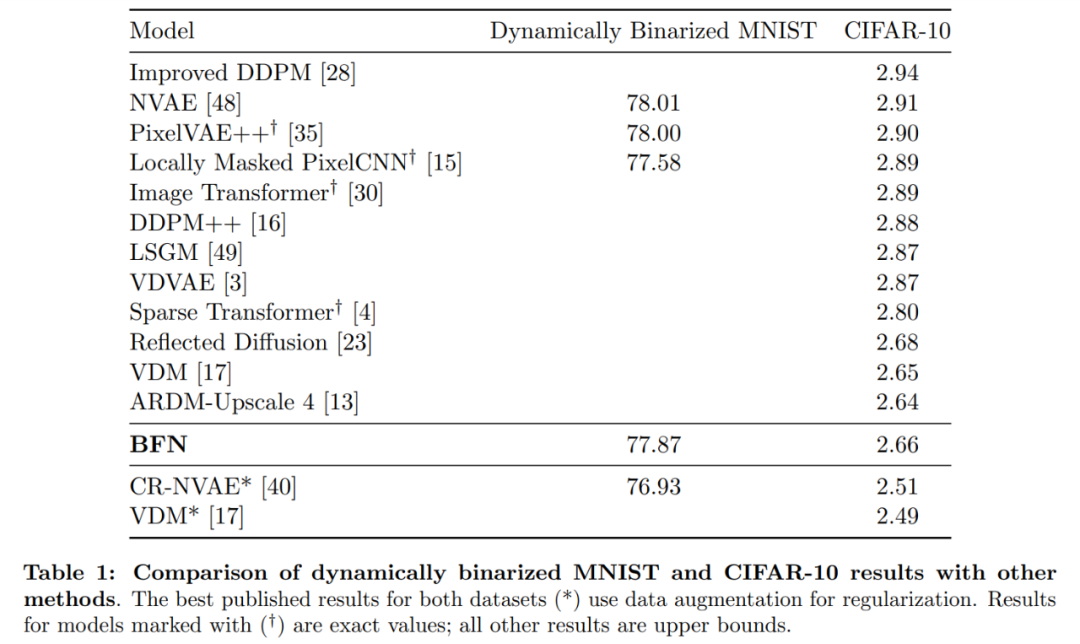
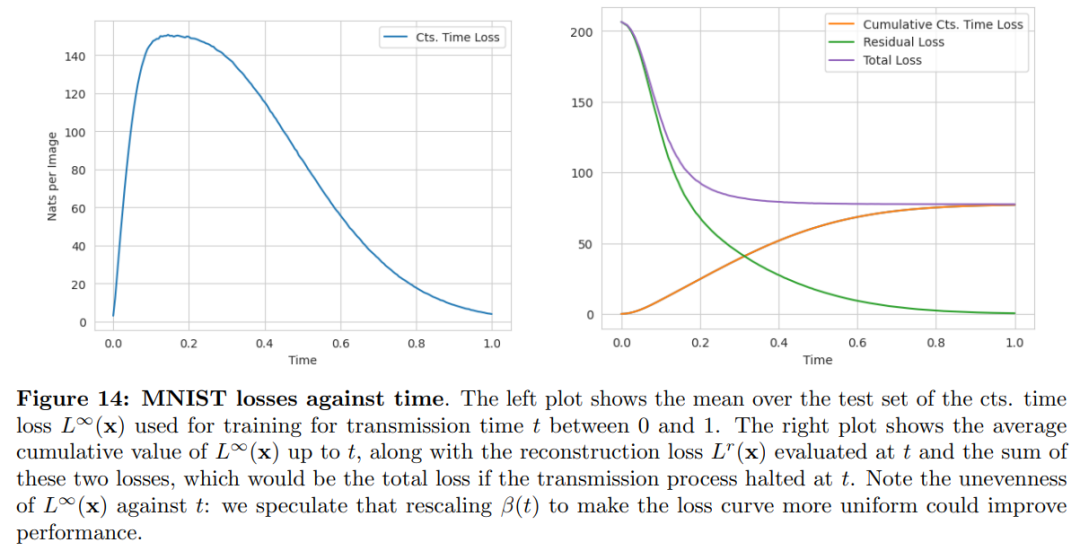
下图为 MNIST 损失曲线:表明对于二进制数据,准确率时间表不是最优的。
CIFAR-10
该研究在 CIFAR-10 上进行了两组生成建模实验,一组 bit-depth 为 8 ,对应于颜色通道有 256 个离散 bin,另一组 bit-depth 为 4 ,对应于颜色通道为 16 个 bin。
表 3 显示,对于 16 bins,离散损失比连续损失提供了更好的性能,并且训练时间也快得多。这一结果对应了这样一个假设,即 bin 相对较低时,使用离散损失进行训练是最有益的。此外,对于 16 和 256 个 bin,当步数 n 较低(例如 10 或 25)时,离散训练会给出更好的结果。然而,在 256 个 bin 上,连续损失比离散损失具有更好的性能。
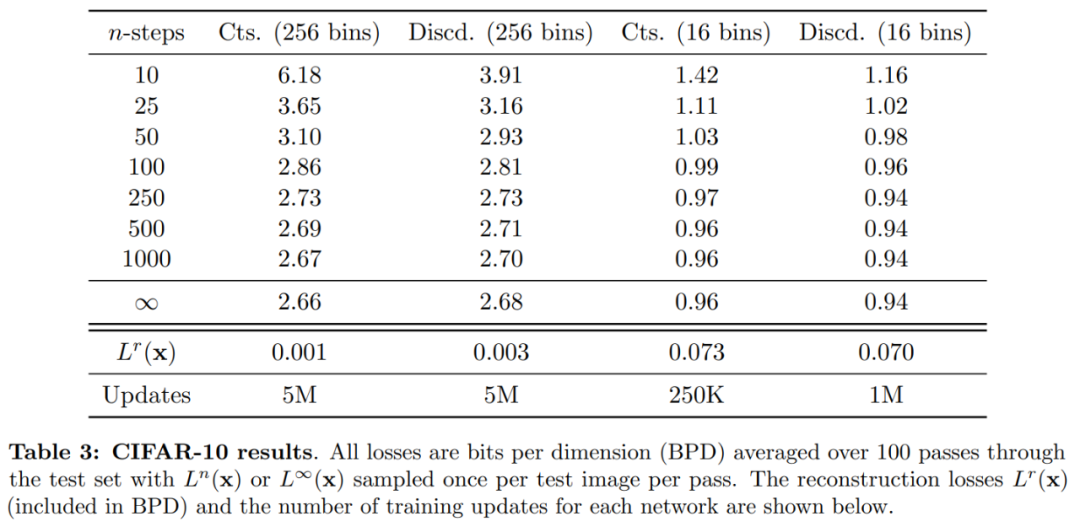
图 15 显示,使用 16 个 bin 进行离散训练比使用 256 个 bin 进行离散训练可提供更好的样本质量。

TEXT8
表 4 显示,BFN 在 text8 测试集上产生了 1.41 BPC,这比其他文献中发现的所有离散扩散模型都要好,并且接近最佳模型 MAC(1.40 BPC)。
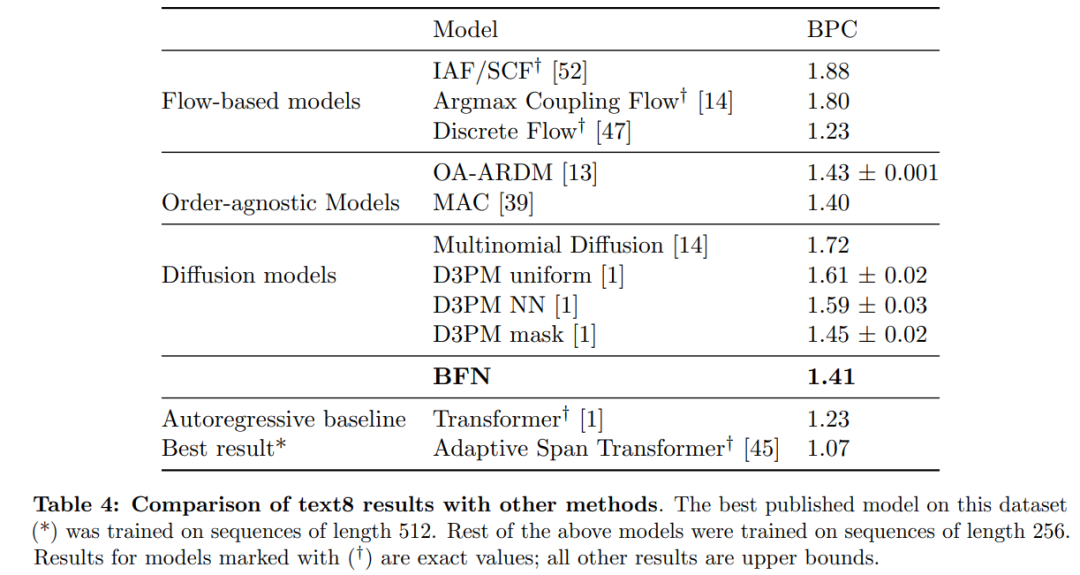
表 5 显示,对于步数 n 的减少,BFN 的性能还是相当稳健的,只需 100 步即可达到 1.43 BPC。通过离散时间损失训练可能会改善这个结果。