前言
现在不仅各大编程语言卷,也顺带感染了C#的内卷。有人面试被问到,汉诺塔算法.这个算法比较有意思。网上C语言较多,本篇来看下C#。
概括
汉诺塔,据说一个古印度的黄金碟片的游戏。把一根柱子上叠好的一堆碟片从小到大的顺序,借助第二根柱子挪到第三根柱子上。
注意这里有几个点
其一:碟片的数量
其二:三根柱子
其三:从小到大借助挪动
其四:小碟片必须在大碟片之上,任何一个。
应该如何做呢?碟片的数量未知,这里假设为n(int)。三根柱子(字符类型),第一根柱子one,第二根柱子two,第三根柱子three。作为参数,可以构建如下函数,函数名为:Hannuo:
static void Hannuo(int n, char one, char two, char three)
{
}柱子之间碟片的挪动,另取一个函数,用以记录:
static void move(char x, char y)
{
Console.Write(x + "->" + y + "\r\n");
}假设只有一个碟片,直接从柱子1挪到柱子3即可,所以函数里面需要判断下:
static void Hannuo(int n, char one, char two, char three)
{
if (n == 1) move(one, three);
}如果大于1个碟片,假设为n。则遵循先把n-1个碟片从小到大的顺序从柱子1借助柱子3挪到柱子2,然后把剩余的最后一个碟片从柱子1挪到柱子3,最后把柱子2的n-1个碟片从小到大的顺序借助柱子1挪到柱子3,完成整个过程。完成代码如下:
static void Hannuo(int n, char one, char two, char three)
{
if (n == 1) move(one, three);
else
{
Hannuo(n - 1, one, three, two);
move(one, three);
Hannuo(n - 1, two, one, three);
}
}整个的代码:
static void Hannuo(int n, char one, char two, char three)
{
if (n == 1) move(one, three);
else
{
Hannuo(n - 1, one, three, two);
move(one, three);
Hannuo(n - 1, two, one, three);
}
}
static void move(char x, char y)
{
Console.Write(x + "->" + y + "\r\n");
}
static void Main(string[] args)
{
Hannuo(3, 'A', 'B', 'C');
Console.ReadLine();
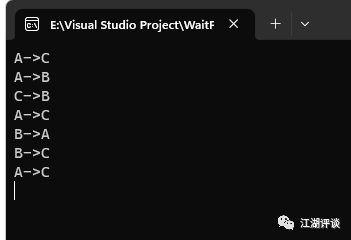
}这里的Main函数,里面传递了3个碟片,然后分别以字符串A,B,C代表三根柱子,进行碟片移动最终的结果是如下:
 图片
图片
三个碟片在三根柱子,A,B,C上进行了7次挪动。其它以此类推。这里面主要是递归算法。