谷歌在KDD 2023发表了一篇工作,探索了推荐系统ranking模型的训练稳定性问题,分析了造成训练稳定性存在问题的潜在原因,以及现有的一些提升模型稳定性方法的不足,并提出了一种新的梯度裁剪方式,提升了ranking模型的训练稳定性。下面给大家详细介绍一下这篇文章。
1、模型背景
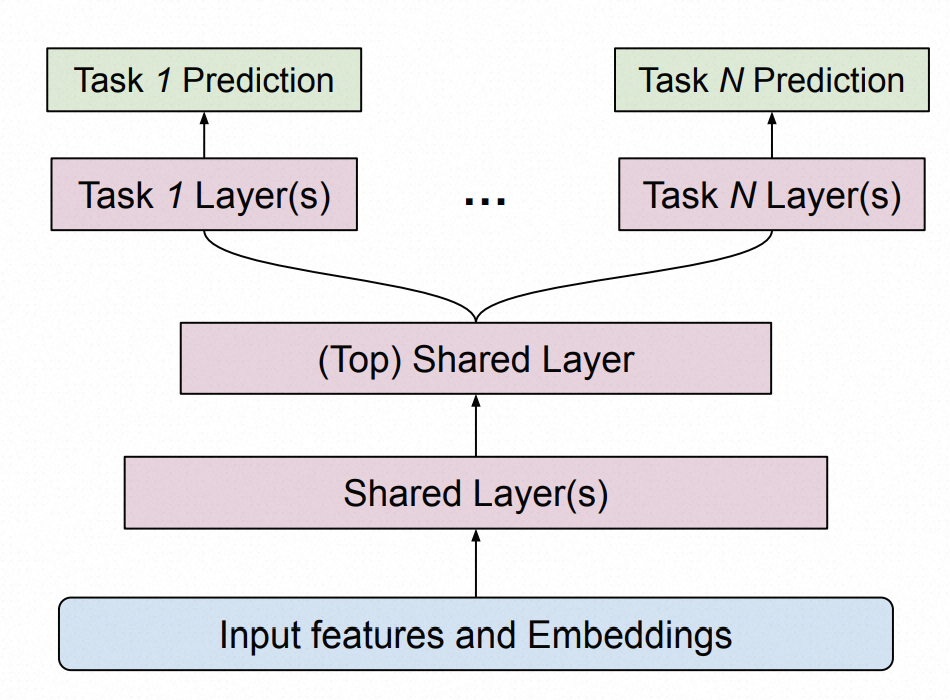
本文以Youtube中的ranking模型为例,进行推荐系统ranking模型训练稳定性的分析。整体模型如下图所示,包括特征输入层、多任务共享层、每个任务私有参数层,整体包括CTR预估、CVR预估等多个任务联合训练。
 图片
图片
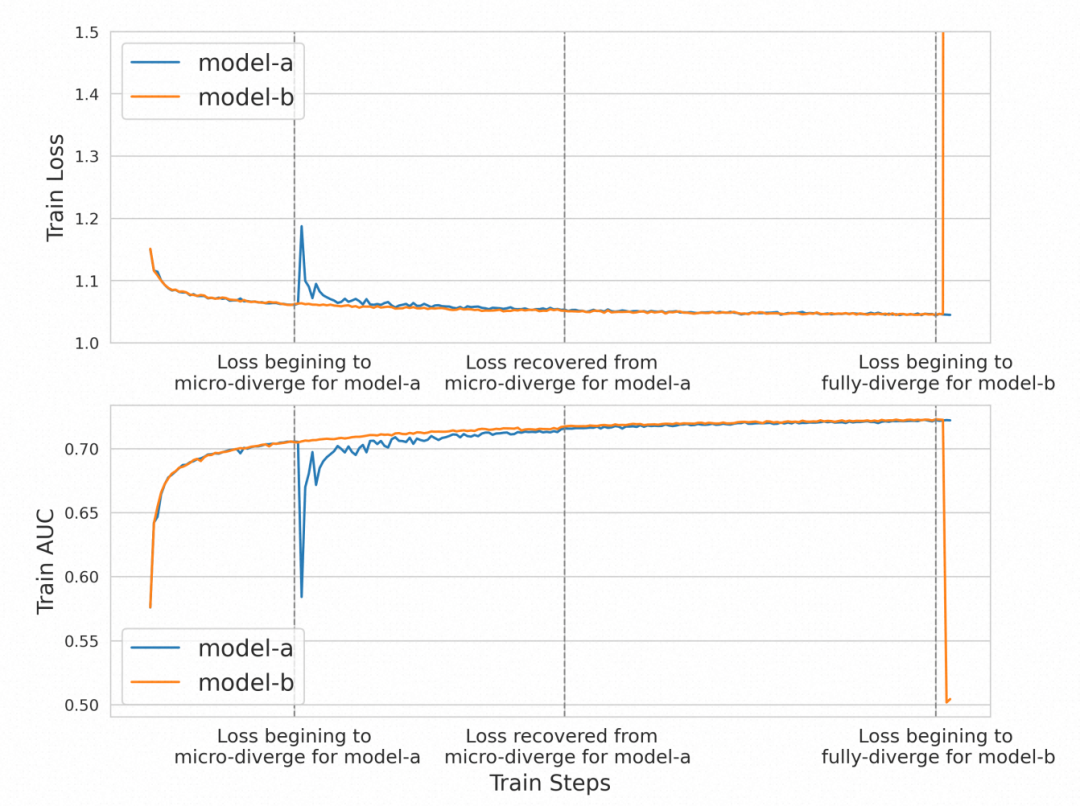
什么样的训练过程是稳定性比较差的呢?如下图所示,model-a的loss和auc曲线被文中称为micro-diverged,即训练过程中出现loss的突增,伴随着auc下降,但是继续训练模型会恢复回来,最终不会影响模型效果。model-b的loss和auc曲线被文中称为fully-diverged,即模型训练过程中出现大幅度的loss增加和auc下降,并且后面也不会再恢复了,对模型的性能影响很大。本文更关注的是后面fully-diverged这种情况。
 图片
图片
2、影响稳定性的因素
为什么推荐系统中的模型,存在这样的训练稳定性问题呢?训练过程不稳定,本质原因在于模型在优化到一个比较陡峭的超平面时使用了一个较大的学习率,导致模型参数的更新出现严重问题,文中原话是“step size being too large when loss curvature is steep”。在推荐系统的ranking模型中,这种现象更为常见,主要由于以下几个原因:
多任务学习:推荐系统中的ranking模型经常采用多任务学习的方式,这导致当一个任务的梯度出现问题时,对共享参数层也会造成很大影响,增加了模型训练不稳定的可能性;
Sequential training:ranking模型经常需要进行ODL或者增量更新,以适应线上数据分布的实时变化。这就导致模型的训练数据一直是动态变化的,模型需要不断拟合变化的数据分布,给模型的收敛带来更大的不确定因素;
模型尺寸和输入特征:相比其他领域的模型,ranking模型需要更多类型的输入特征,并且目前的趋势是不断增大模型尺寸,这些都可能导致模型的优化超平面变得更加陡峭导致难以收敛。
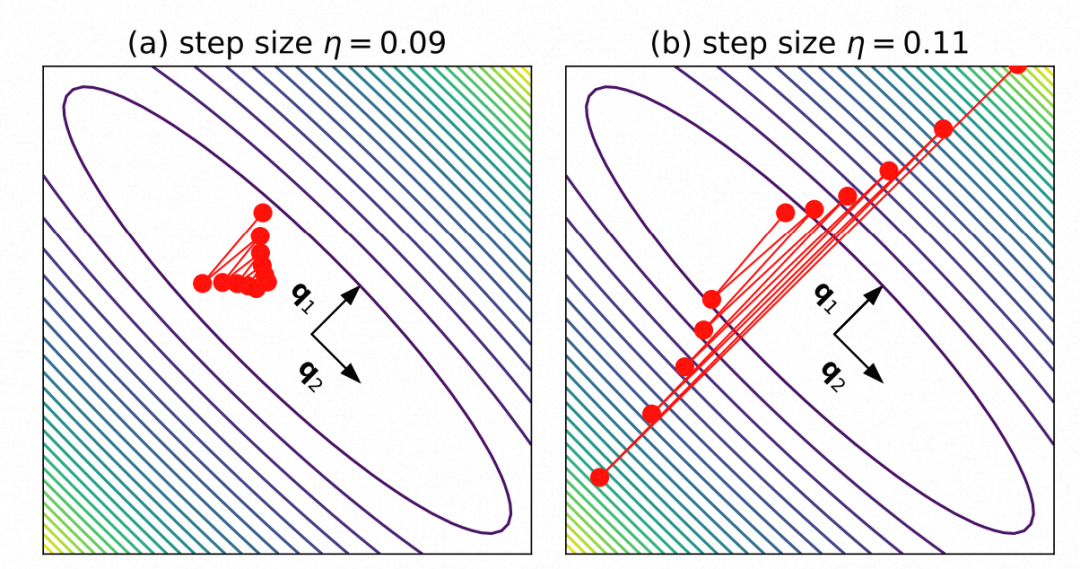
下图展示了在相同的学习率下,loss平面的陡峭程度对于梯度更新的影响,越陡峭的超平面,以一个不适配(较大)的学习率更新会导致loss震荡难以收敛。
 图片
图片
3、现有方法
为了解决这类训练不稳定问题,业内已经有一些相应的解决方案。例如,针对上述Sequential training需要适配数据分布而带来的不收敛问题,可以采用滑动时间窗口的方式生成训练样本。每次让模型使用滑动窗口内的数据进行训练,通过增大滑动窗口的尺寸,可以让每轮训练的模型见到的数据分布差异没那么大,平滑的更新数据分布,缓解模型需要适配数据分布剧烈变化的问题。
不过,从本质原因“step size being too large when loss curvature is steep”来讲,一个治标治本的方法是直接优化梯度更新的过程,对于陡峭的loss超平面使用更小的学习率,使用Hessian矩阵最大特征值计算,也可以近似利用梯度代替。Adagrad和梯度裁剪就是这类方法中的经典工作。Adagrad通过每个参数历史的梯度更新情况进行累计,来调整每个参数的学习率,历史更新较多的参数,学习率设置的更小一些,梯度更新公式如下所示:
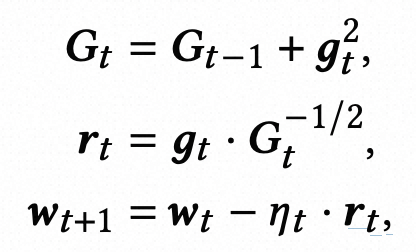 图片
图片
而梯度裁剪更加直接,如果计算的梯度大于一定的阈值,就将梯度缩小(如下面公式,核心是缩放系数sigmoid的计算,根据阈值和梯度的L2范数比值而来,梯度的L2范数太大就缩小梯度)。
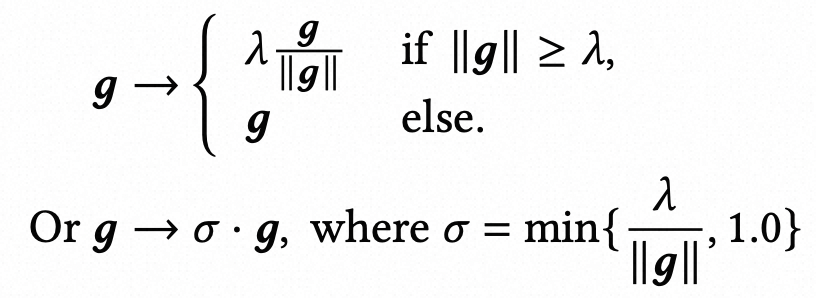 图片
图片
如何设计梯度裁剪中的阈值呢?后续的工作Adaptive Gradient Clipping提出了一种自动设计阈值的方式,核心思路是梯度的范数与模型参数范数比值不能太大,因此引入这一项帮助个性化调节不同参数的梯度:
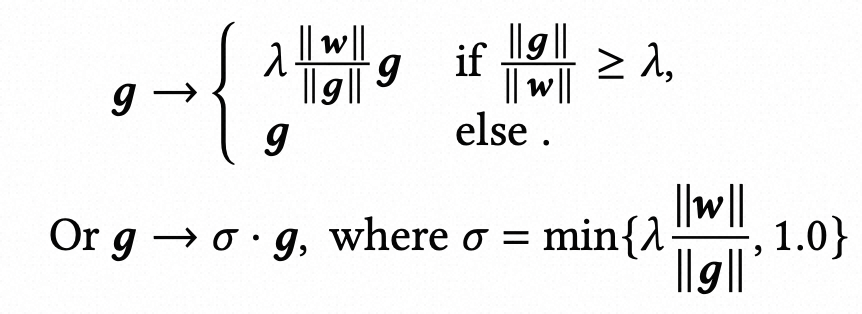 图片
图片
4、本文方法
虽然上述梯度裁剪方法有助于提升ranking模型训练稳定性,但是文中发现这类方法对于推荐系统中的ranking模型并不能起到有效作用。经过分析,文中发现,之前的梯度裁剪方法在梯度突然暴增的时候控制力不够。文中提出了Clippy,主要修改的是梯度裁剪中的缩放系数,相比原来的梯度裁剪主要有2个改进点,一方面将L2 norm改成了无穷范数(取各个维度L1最大值),同时对于分子改成了上文adagrad中的r,即历史梯度的累积。
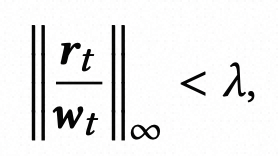 图片
图片
这样修改的原因为,如下图所示,在step-b到step-c损失函数突增,梯度对应变大,但是之前的梯度裁剪方法得到的缩放系数并不足以控制梯度。将L2范数改成无穷范数,可以方便捕捉某一个维度上的突变,对某一维度的梯度突增有更强的敏感性。另外,将分子变为累计梯度,让模型根据累计梯度而不是当前梯度调整阈值,更适配Adagrad对模型参数的更新过程。通过这种方式,如下图第二列所示,对梯度的约束更加强烈,可以有效限制梯度过大导致的训练不稳定问题。
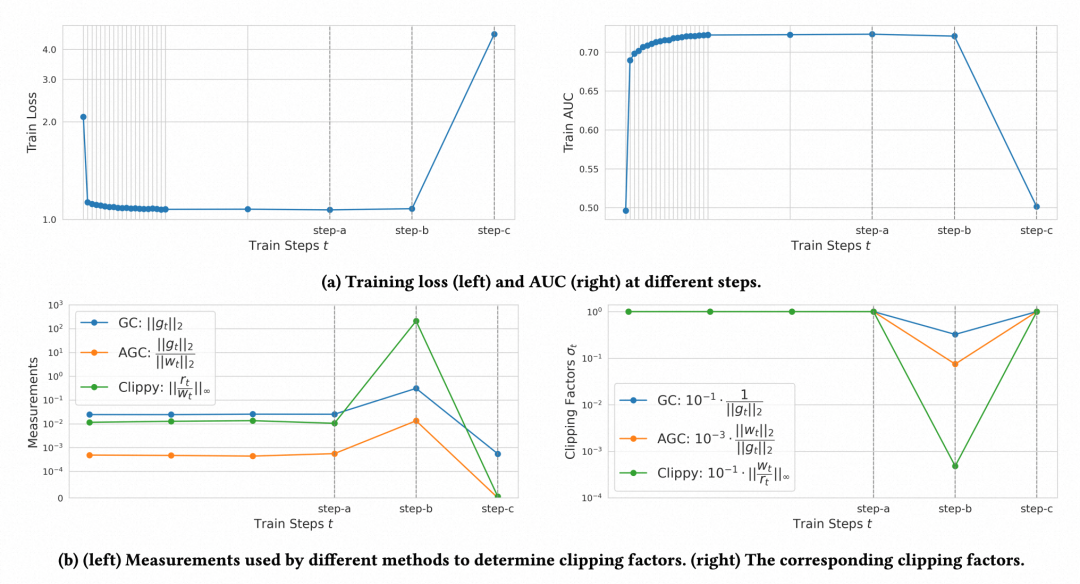 图片
图片
最后,文中给出了Clippy加入到Adagrad更新的整体算法流程,如下表:
 图片
图片
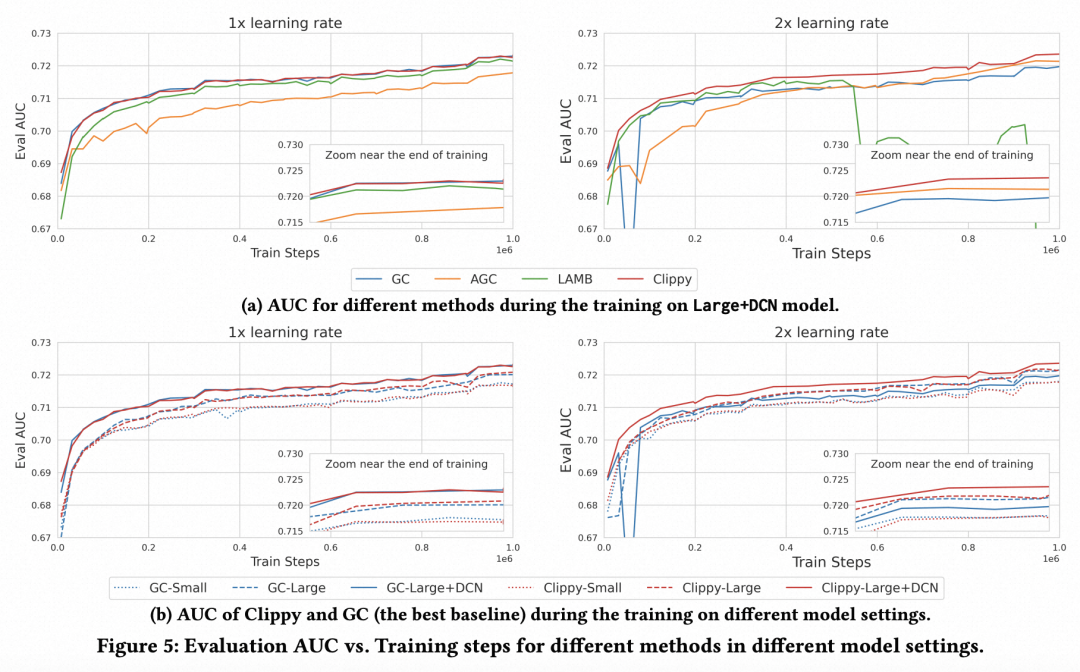
通过下面的实验对比可以发现,使用了Adagrad+Cliipy后,模型的训练过程更加稳定: