50年前的kNN算法,只用14行代码在文本分类上超越风头正盛的Transformer,包括BERT——
这个来自ACL Finding的成果,一发布就火爆学术圈,让人重新思考还有多少旧方法可以用于今天的机器学习任务。
 图片
图片
有人盛赞它的创意性超过95%的同会论文,但是却没有获奖实在令人想不通。
 图片
图片
短短14行代码,完全打开了大家的思路。

然而,才不到几天的时间,就有人发现:
这一切好像都是个误会。
BERT没有被打败,代码有bug,结果有问题!
 图片
图片
这是,反转了???
重测后性能从SOTA变最差
先再来简单回顾一下这篇论文的主要背景和思想:
 图片
图片
它讲的是如今由于精度高被经常用于文本分类的深度神经网络模型(DNN),因为其计算密集型的特性,需要数百万个参数和大量标记数据才能保证效果,这就导致它用起来或者做优化,以及转移到分布外数据等情况时都很费钱。
在此,来自滑铁卢大学和AFAIK机构的研究人员,就“突发奇想”提出了一种不需要参数的替代方案:
将简单的压缩算法比如gzip和k近邻分类算法进行结合来做这件事(用到了归一化压缩距离NCD)。
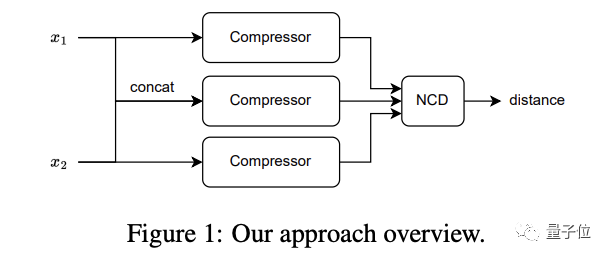 图片
图片
结果,这种简单的方案在没有任何训练参数的情况下,效果居然很不错——
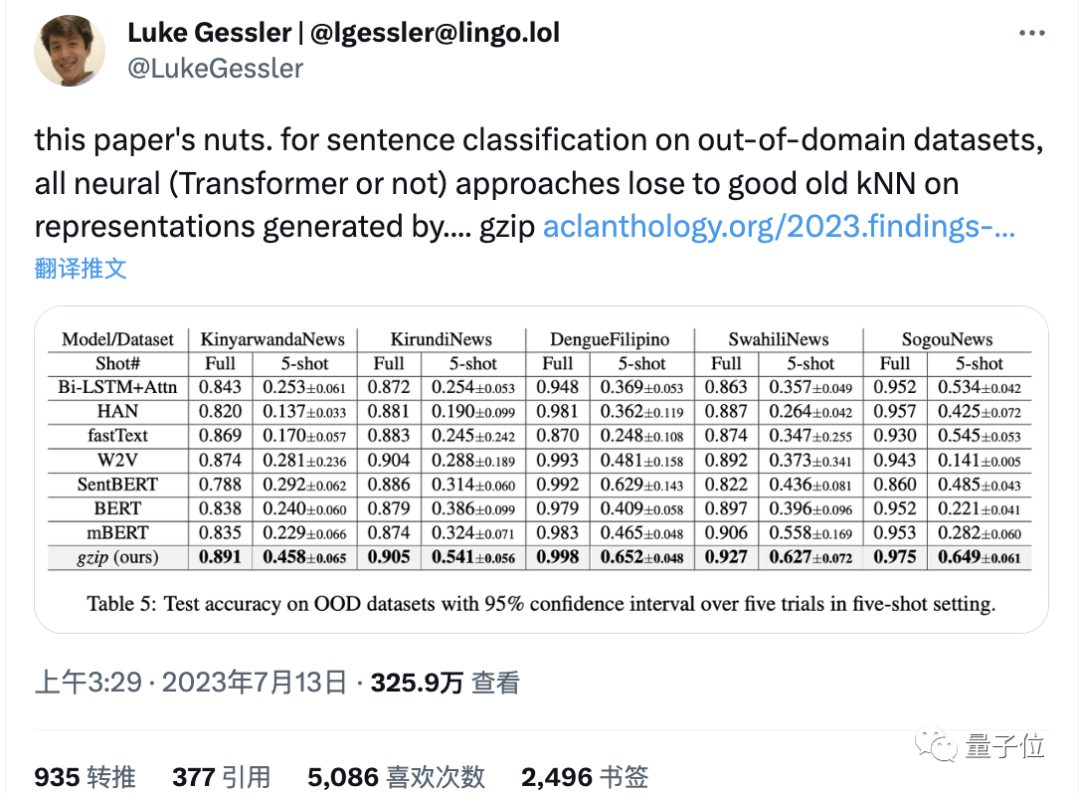
在7个分布内数据集上有6个结果与各类DNN相媲美,在分布外数据集上的结果则接连5把胜出,把BERT都给打败了。
而且它在少样本情况下也好使,相反此时的DNN却因为标记数据太少根本无法进行有效训练。
来自于美国的机器学习研究员Ken Schutte(博士毕业于MIT电气工程与计算机科学),在看到这篇论文后非常感兴趣,并冒出了一些新点子。

于是他并决定复现一下。
结果,就出现了蹊跷:
我发现(当然我也不敢保证),方法中的kNN代码中似乎存在一个错误(也可能是无意的),导致最终测试结果的准确度指标其实都全部高于了预期。
“太长不看”概括一下就是:结果用的是top-2精度,而不是本应该的kNN(k=2) 精度。
也就是说,它的效果可能并没有那么强。
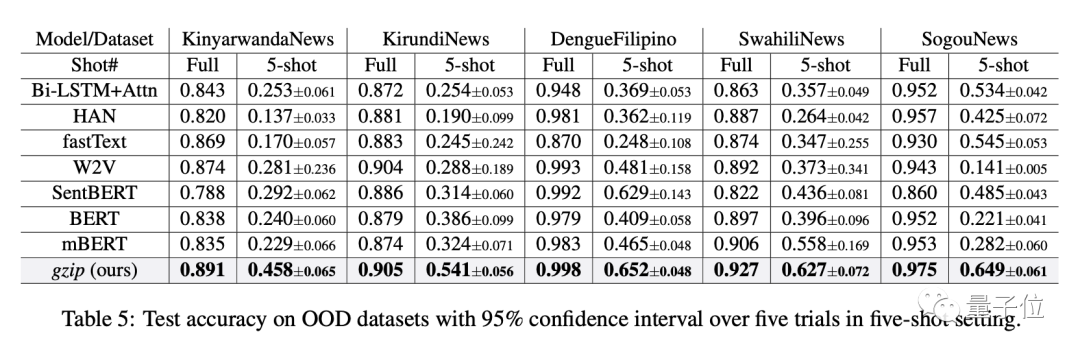
具体而言,Ken指出,在论文的表5中,结果显示该方法在OOD数据集上打败了所有其他基于神经网络的方法:
 图片
图片
而他对前四个数据集都重新进行了一遍测试(使用kNN(k=2) 精度),结果有很大出入,根本无法打败那些基准模型,甚至从性能最佳变为性能最差。(最后一个数据集因为太大Ken还没尝试)

下面是详细解释。
在论文中,作者在使用kNN分类器时,都是取值k=2。
(kNN是一种有监督算法,通过“有标签”的样本最终确定未知样本的类别,该算法主要参数就是k值的选择,k值越大,分类效果越稳定,但计算量也越大)
Ken认为,这个选择有点没必要,不会给分类器增加太多信息,取1就行。
而当取2时,在训练集中搜索出的两个近邻点类别标签不一致的情况下,比如一个是正类,一个是负类,那么就产生了平局情况,我们需要进一步确定唯一正确的那个点。
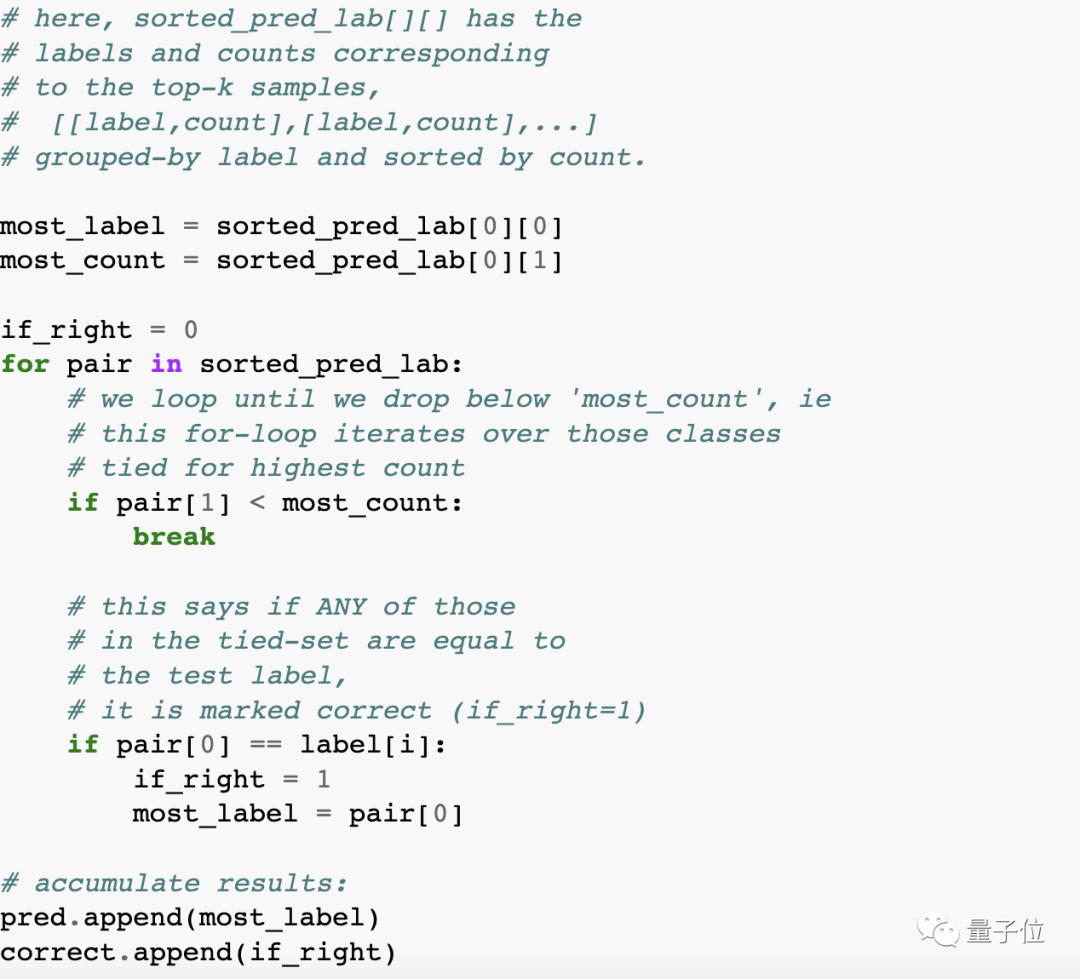
在这个确定的过程中,论文中的源码(位于experiments.py文件中的calc_acc方法中)出现了问题:
 图片
图片
简单来说就是,这段代码的做法其实是只要2个近邻点标签中有一个与中心点真实类别一致(简而言之,有一个对就算对),就判断为正确,这也就相当于Top-2精度。
但标准的KNN算法,会使用其他打破平局的策略,比如距离近的类别优先,或随机选取来确定,也就是采用标准的kNN(k=2) 精度来评估结果,“更严格”。
这就导致在k=2时原方法计算的准确率其实是高于标准算法的,也就是最终效果并没有现在我们看上去的那么牛。
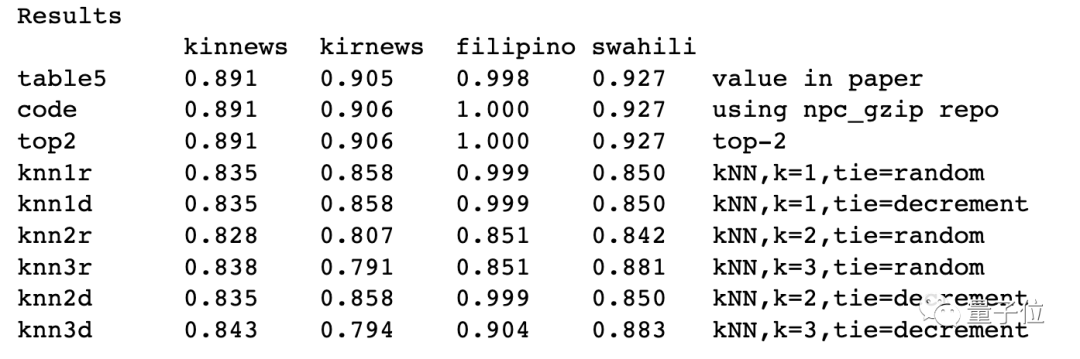
这不,Ken重新写了两种打破平局的策略(一个是随机选择,一个是递减k),重新计算了各数据集下模型的准确率,结果均出现了不同程度的下滑:
 图片
图片
当然,我们可以发现,如果还是按照top-2算,Ken复现的结果基本和原论文没有差别,侧面证明Ken的发现是有效的。
网友:虽然但是,不影响方法本身的创新性
这个消息出来之后,网友是怎么看的呢?
有意思的是,大家都觉得Ken的分析很有道理,但这不影响该方法本身的创新性。
尽管没有打败BERT,但其思想还是令人印象深刻。
作者这个策略也没有很不合理啦,最重要的是后面还会有更多探索这个研究方向的论文出来。
 图片
图片
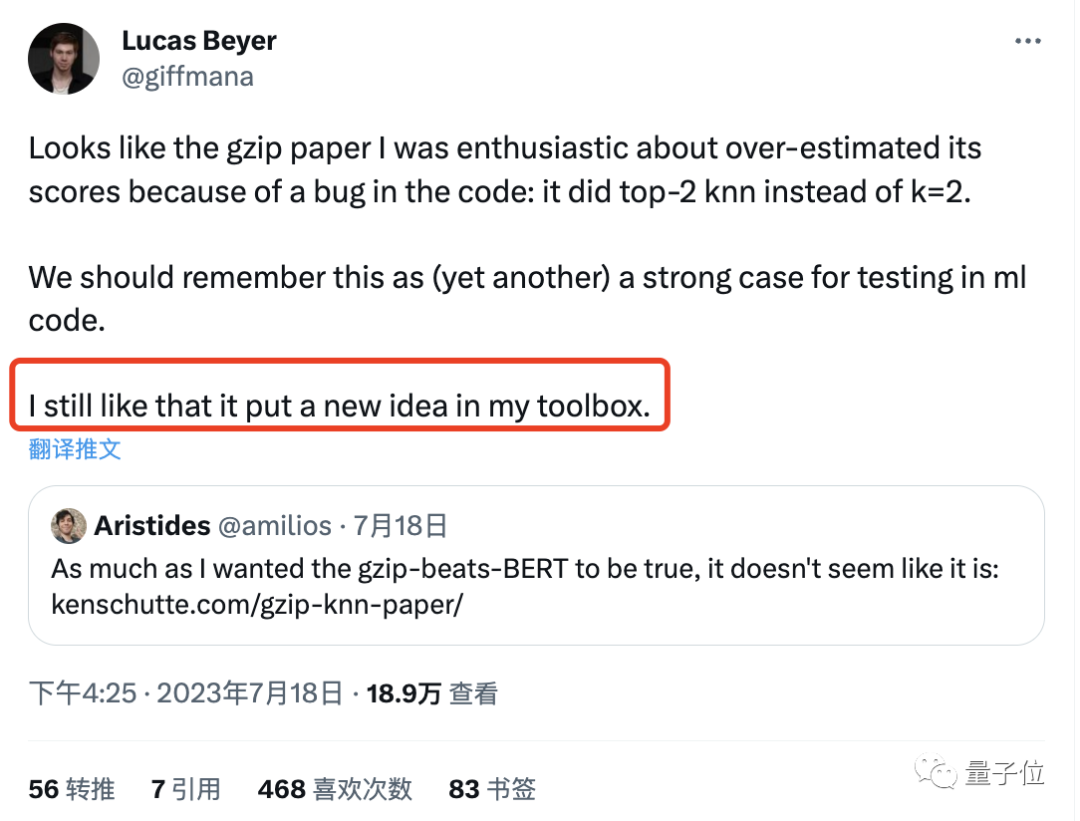
GoogleAI的研究员Lucas Beye也表达了类似的意思。
 图片
图片
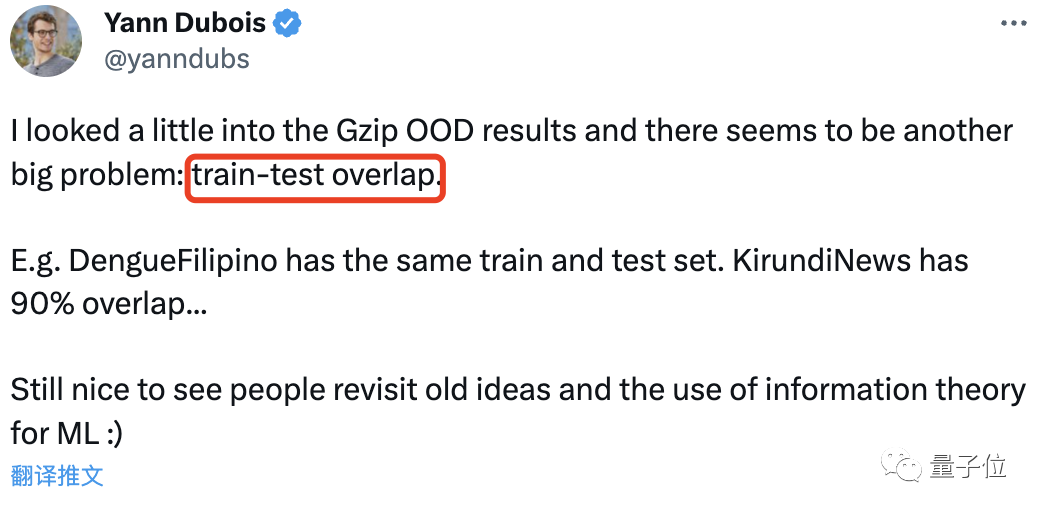
值得一提的是,在Ken之后,斯坦福博士Yann Dubois又发现该论文的问题还不止如此——
其训练测试集也重叠了。
比如DengueFilipino的训练集和测试集完全一样,而KirundiNews的重复率也高达90%。
 图片
图片
当然,一如既往,由于该方法实在是太特别了,尽管网友评论中也充斥着“wtf”这样的声音,但大部分人还是坚决捍卫它的重要贡献,认为问题不大,可能只是审查不到位等等。
这不,“你可以扼杀一篇论文,但你无法扼杀一个想法”的评论都出来了。
 图片
图片
大家怎么看?这两个bug影响你对这篇论文的看法吗?
Ken原博:https://kenschutte.com/gzip-knn-paper/
原论文:https://aclanthology.org/2023.findings-acl.426/



































