美团一面：循环队列听说过么，怎么实现？-51CTO.COM

顺序队列

顺序队列定义

队列的底层是数组，我们常说的队列其实就是顺序队列，其数据结构定义一般是：

队头指针指向数组第一个元素
队尾指针指向数组最后一个元素的下一个位置

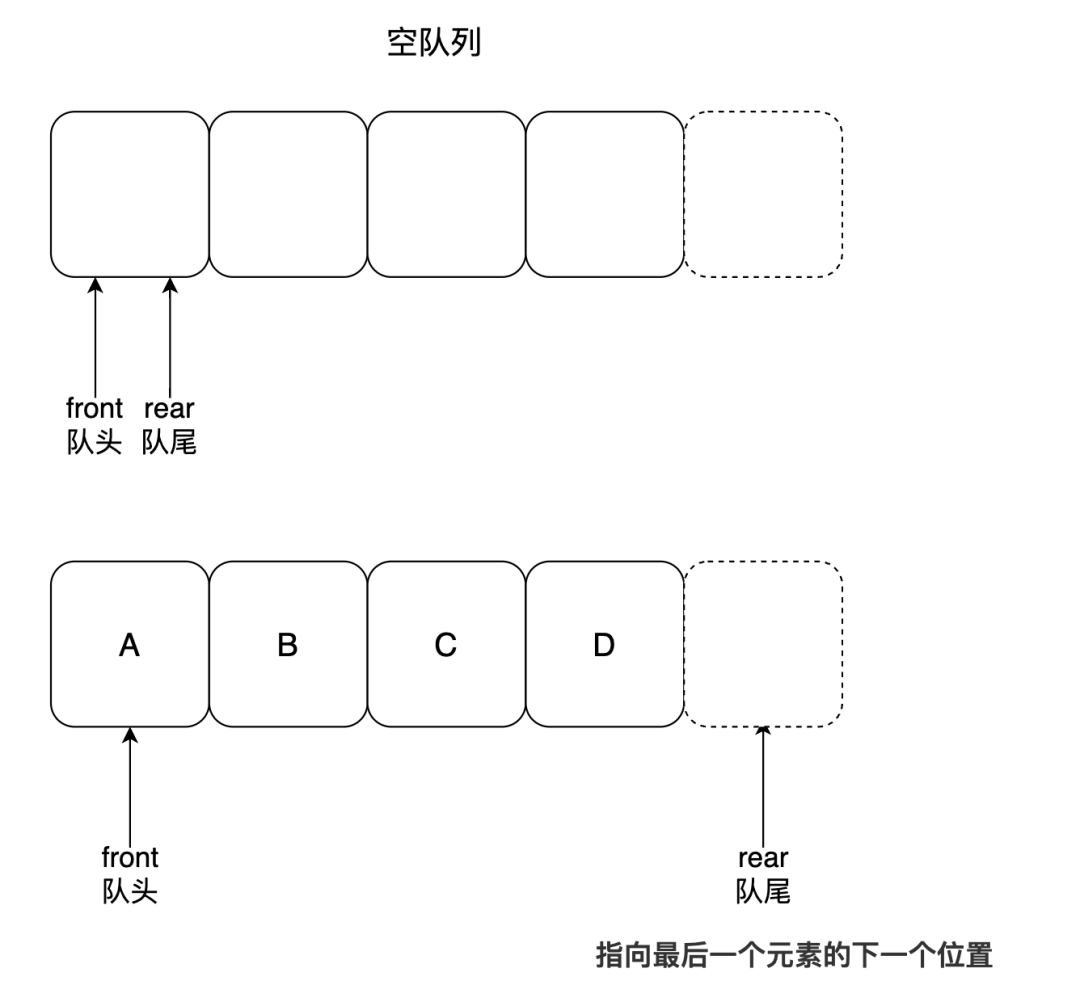
为了避免当只有一个元素时，队头和队尾重合使处理变得麻烦，所以这里引入了队头和队尾两个指针，假设 front 指针指向队头元素，rear 指针指向队尾元素的下一个位置，这样：

当 front == rear 时，表示这个队列是空队列
当 front == rear + 1 时，表示这个队列中只有一个元素

示意图如下：

图片

众所周知，队列是先进先出的，那么进队操作对应的步骤就是：先送值到队尾，再将队尾指针 +1

// 送值到队尾
queue[rear] = x;
// 队尾指针 +1
rear ++;

出队操作：先取出队头元素，再将队头指针 +1

// 取出队头元素
x = queue[Q.front]
// 队头指针 +1
front ++;

假溢出问题

顺序队列存在假溢出问题，就是明明在队列中仍然有可以存放元素的空间却无法执行入队操作了，举个例子：

队列的大小是 5（数组容量为 5），一开始是空队列，然后依次入队了 A、B、C、D：

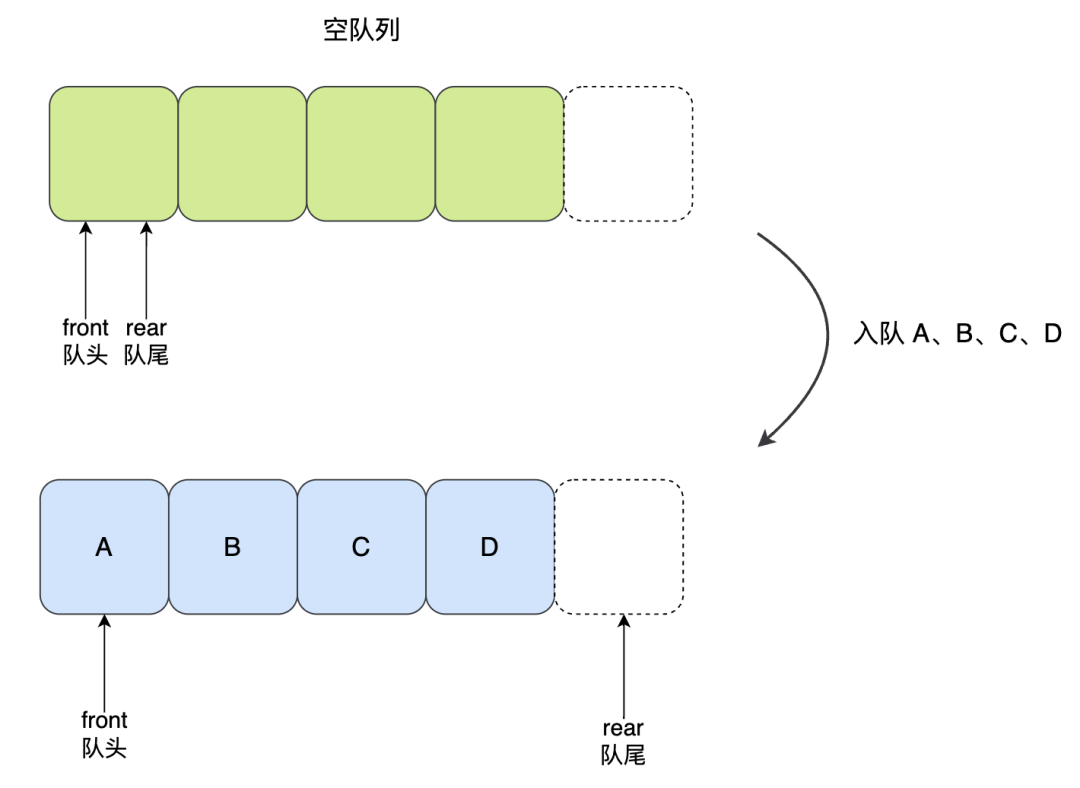图片

然后 A 出队，B 出队，相应的 front 指针会往后移动两位：

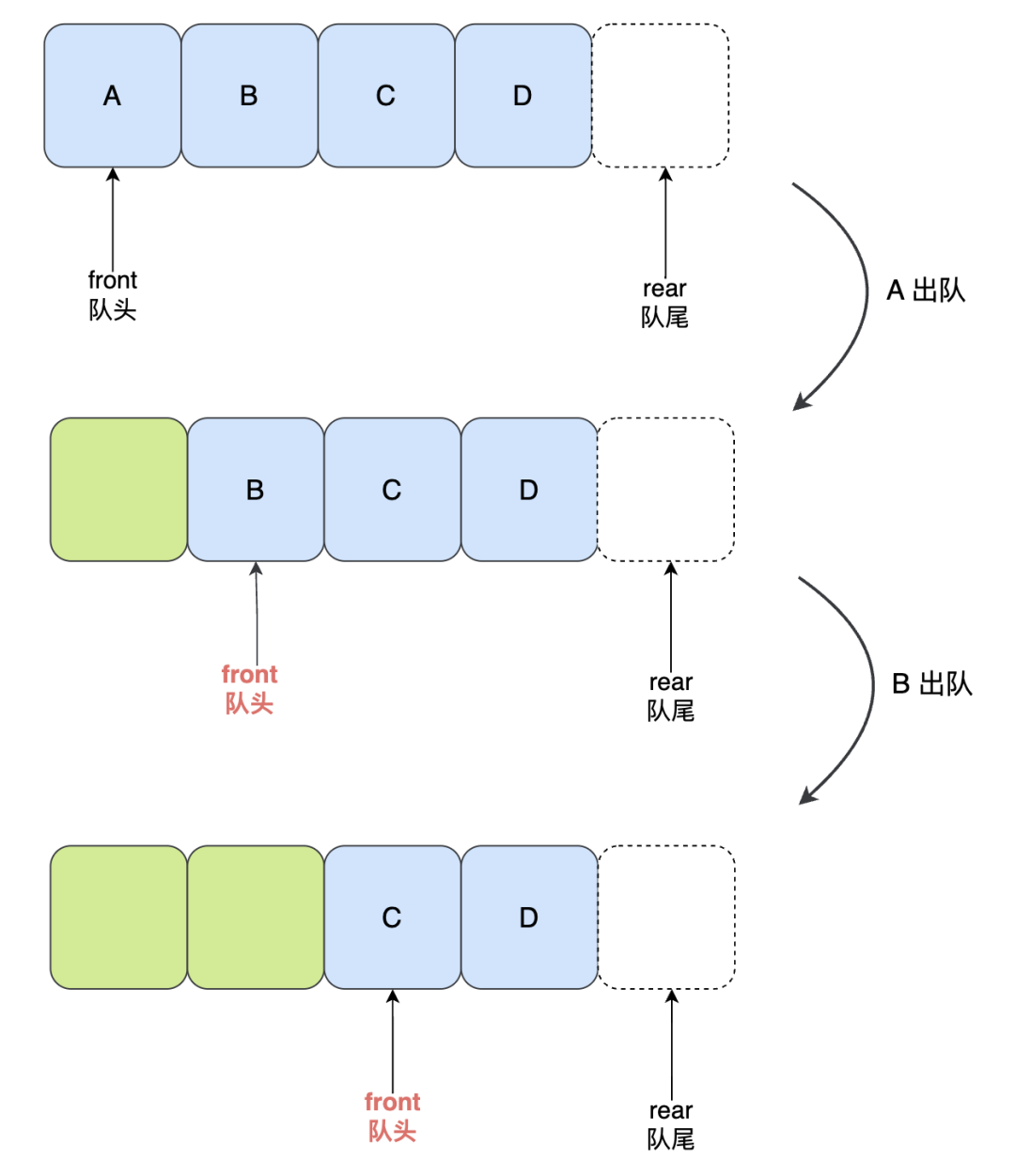图片

再入队一个新元素 E，此时 front 指针不变，rear 指针需要 +1，已经超出了数组的下标范围，就会导致新元素插入失败：

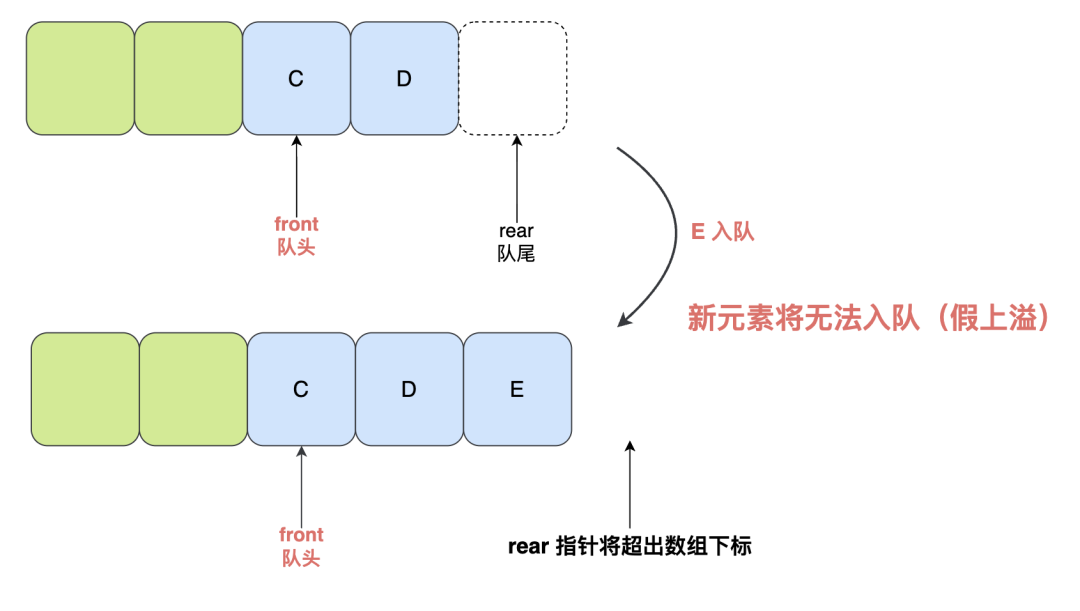图片

明明队列中还有空间，插入元素竟然会失败？这就是一种假性上溢出现象。

如何解决这个问题呢，有三种：

建立一个足够大的存储空间以避免溢出。这样做空间使用率低，浪费存储空间
移动元素：每当出队一个元素，就将移动队列中所有的已有元素向队头移动一个位置。这样做很明显时间复杂度比较高，效率慢
循环队列：将队头和队尾看作是一个首尾相接的循环队列

因此，循环队列是解决顺序队列假溢出问题的最佳选择！

循环队列

循环队列的数据结构定义一般是：

队列长度固定，即队列（数组）容量有限
队列的头尾相接形成一个环，当队尾到达数组的最后一个位置时，下一个位置是数组的第一个位置

具体实现步骤如下：

定义一个数组和两个指针：front 和 rear，分别表示队头和队尾的位置。初始时（空队列），队头和队尾都指向数组的第一个位置，即 front = rear = 0。
入队时，首先检查队列是否已满，如何判断队列满？牺牲一个单元来区分队空和队满：即 (rear + 1) % maxsize = front。如果满了则返回错误，否则将元素添加到队尾，即 queue[rear] = element，然后将 rear 指针向后移动一位，即 rear = (rear + 1) % capacity。
出队时，首先检查队列是否为空，**front == rear 就表示队列空**。如果为空则返回错误，否则将队头元素取出并返回，即 element = queue[front]，然后将 front 指针向后移动一位，即 front = (front + 1) % capacity。
在队列的任何时刻，队列中的元素数量为 (rear - front + capacity) % capacity

示意图如下：

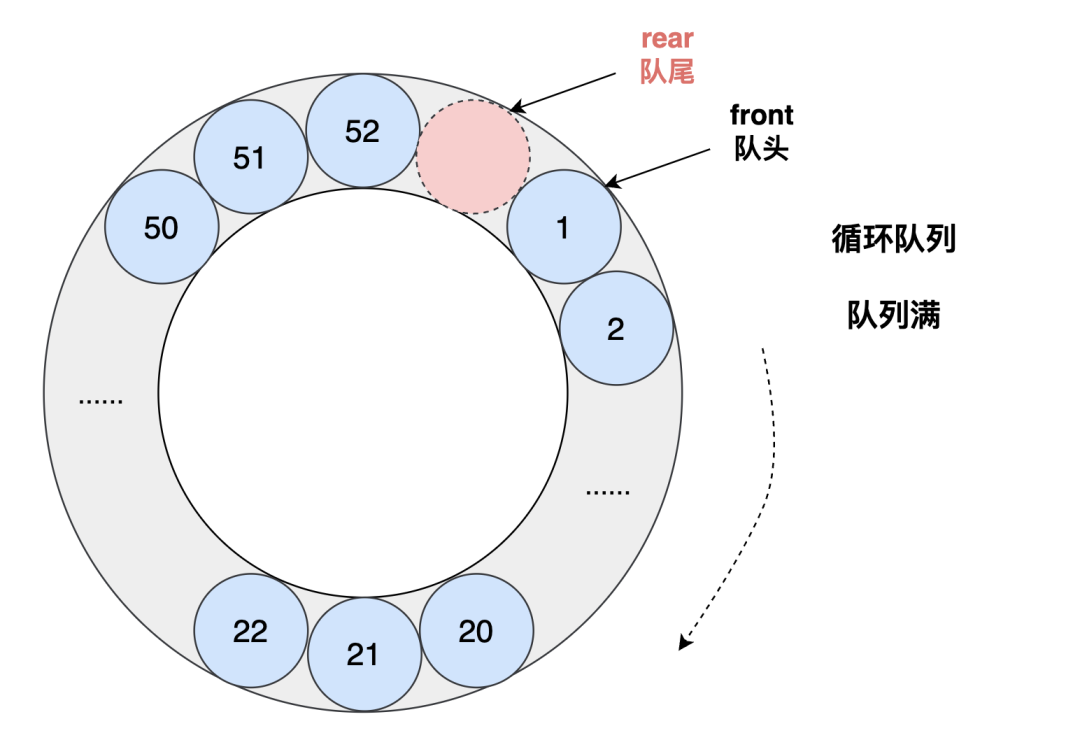图片

以下是一个基于数组实现循环队列的 Java 代码示例：

public class CircularQueue {
   // 存储元素的数组
    private int[] data;
    private int front, rear;
   // 数组大小
    private int capacity;

    public CircularQueue(int k) {
        capacity = k;
        data = new int[capacity];
        front = 0;
        rear = 0;
    }

   // 入队
    public boolean enqueue(int element) {
        if (isFull()) {
            return false;
        } else {
            data[rear] = element;
            rear = (rear + 1) % capacity;
            return true;
        }
    }
 
   // 出队
    public boolean dequeue() {
        if (isEmpty()) {
            return false;
        } else {
            front = (front + 1) % capacity;
            return true;
        }
    }

    // 获取队头元素
    public int front() {
        if (isEmpty()) {
            return -1;
        } else {
            return data[front];
        }
    }
  
   // 获取队尾元素
    public int rear() {
        if (isEmpty()) {
            return -1;
        } else {
            return data[(rear - 1 + capacity) % capacity];
        }
    }

   // 判断队列是否为空
    public boolean isEmpty() {
        return front == rear;
    }
 
   // 判断队列是否满
    public boolean isFull() {
        return (rear + 1) % capacity == front;
    }
}

简单总结就是：

初始/队空：front = rear
出队：front = (front + 1) % capacity (最大元素个数)
进队：rear = (rear + 1) % capacity
队列长度：(rear - front + capacity) % capacity
队满（牺牲一个单元来区分队空和队满）：(rear + 1) % capacity = front