LeCun究竟是经过了怎样的思考,才得出了世界模型是AI大模型未来最理想道路的结论?
很幸运,去年曾听过他在暑假学校关于统计物理和机器学习演讲的学生Ania Dawid,将他的观点仔细地整理和发表出来。
LeCun对于她的工作也表示了盛赞。
这篇笔记解释了当前机器学习方法的局限性,并且介绍了LeCun在2022年的论文<A Path Towards Autonomous Machine Intelligence>中提出的autonomous AI所需的核心概念,以及设计背后的主要思想。
论文地址:https://arxiv.org/abs/2306.02572
类人智能的可能性
在AI达到类人水平并带来新的技术革新之前,当前的自动化系统仍然有重大的局限性。
最理想的情况下,会出现L5自动驾驶、家用机器人、虚拟助理,这些机器人会学习可靠的世界模型,然后进行推理,对复杂的行动序列做出计划。
在这些笔记中,Ania Dawid总结了LeCun提出未来自主智能架构背后的主要思想,引入了基于能力的潜变量模型,在LeCun建议构建的模块——分层联合嵌入预测架构(H-JEPA)中结合了它们的优势。
在过去十年中,机器学习方法迅速普及,ML模型在围棋、国际象棋和Shogi等战略游戏中都表现出了专家级的性能。
作为交换,创建深度学习模型需要在大量数据集上训练,这是一种极端的计算成本。
相比之下,人类的学习却十分高效,我们可以快速直观地找到方法来完成任务,连婴儿都能很快获得对物理世界的直观理解。
如何让AI模型发展出像人类一样的潜能?在这些课堂讲稿中,LeCun与学生们探索了autonomous intelligence的概念。
他们希望能够实现一个充分自主的AI,他通过转移知识和自动适应新情况而在通用任务上表现良好,无需首先尝试很多解决方案。

自主机器智能
当前机器学习的局限性
到目前为止,机器学习系统仍然在很大程度上依赖于SL,这就需要大量的标记样本,而RL需要大量的试验,这在当前的现实中不切实际。在现实世界中,每个行动都需要时间和成本。

相比之下,人类和动物主要依靠对环境的积极观察,并以此建立世界模型。
婴儿就几乎完全通过观察来学习,他们的学习过程与SSL最相似,只有一点点SL(和家长互动)或RL(通过实践尝试各种解释方案)。
实际上,人类是想象和推演大部分结果,而不是全部尝试一遍。
因此,实现完全自主类人智能的道路主要有三个挑战:
1.学习世界的表征和预测模型,使AI系统能够预测未来,特别是自己行动会导致的结果。
最有可能的方法就是自监督学习(SSL),因为SL和RL需要太多的成本或试验。
2.学习以一种与DL兼容的方式推理。推理需要考虑到与前馈潜意识计算相反的意图。最可能的方法就是像energy minimization那样设计推理和规划。
3.学习规划复杂动作序列,这个过程中需要行动计划的分层(hierarchical)表征。
自主智能的新范式
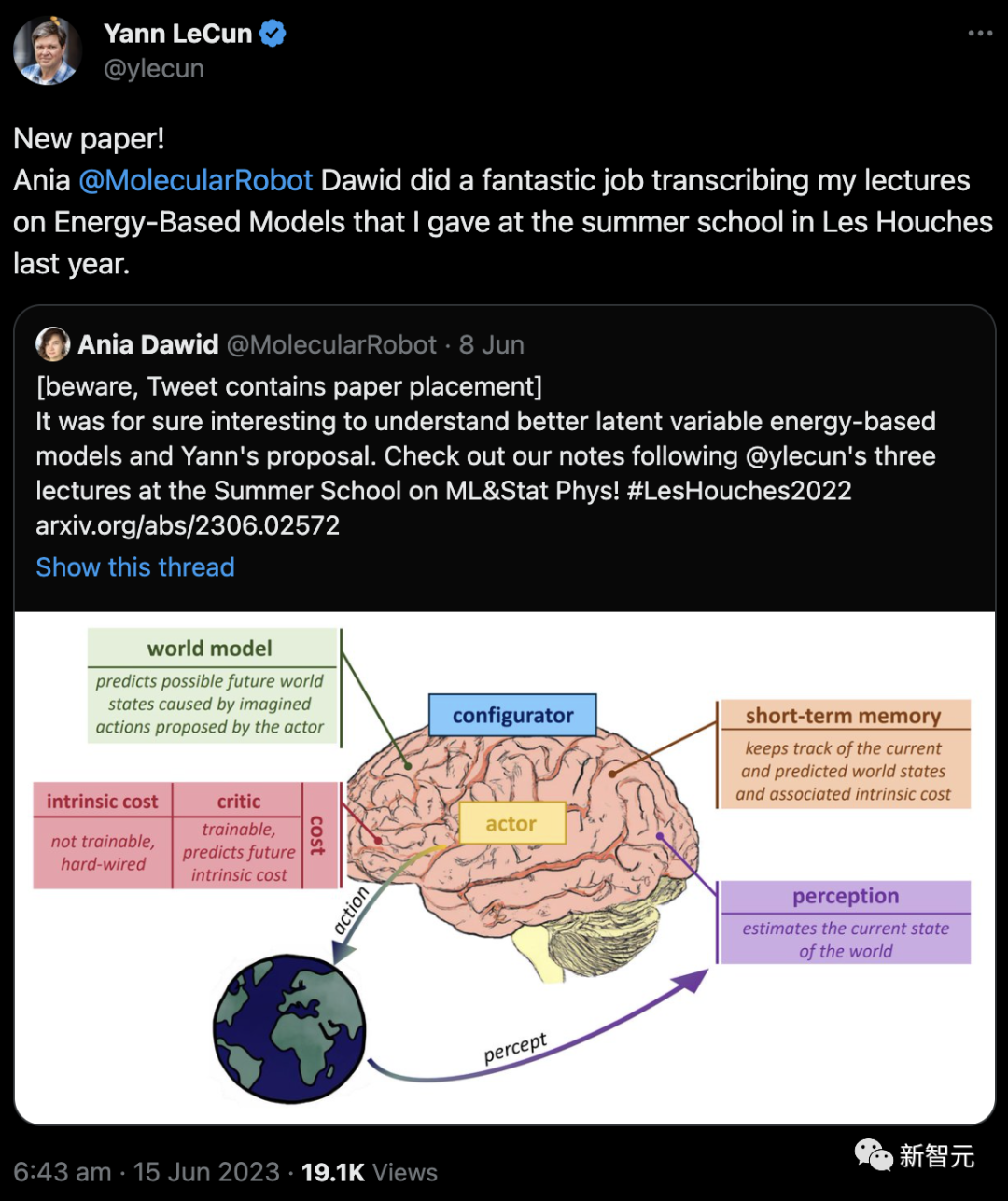
在论文中,LeCun提出了自主AI应该有的模块化结构。
这个AI架构由多个相互连接的模块组成。
Perception模块估计世界的当前状态,actor可以使用该状态,并在world model的指导下提出最佳动作序列,根据actor的动作预测或「想象」未来可能的世界状态。
这些联系被称为「感知-计划-行动循环」。
在想象actor行为的可能后果时,世界模型使用cost推理模块。
它可以分成两个子模块——对痛苦、快乐、饥饿等基本需求进行建模的intrinsic cost,以及预测内在成本未来值的critic。
Short-term memory模块用于预测未来世界状态。Configurator模块通过配置所有其他模块来实现任务之间的切换。
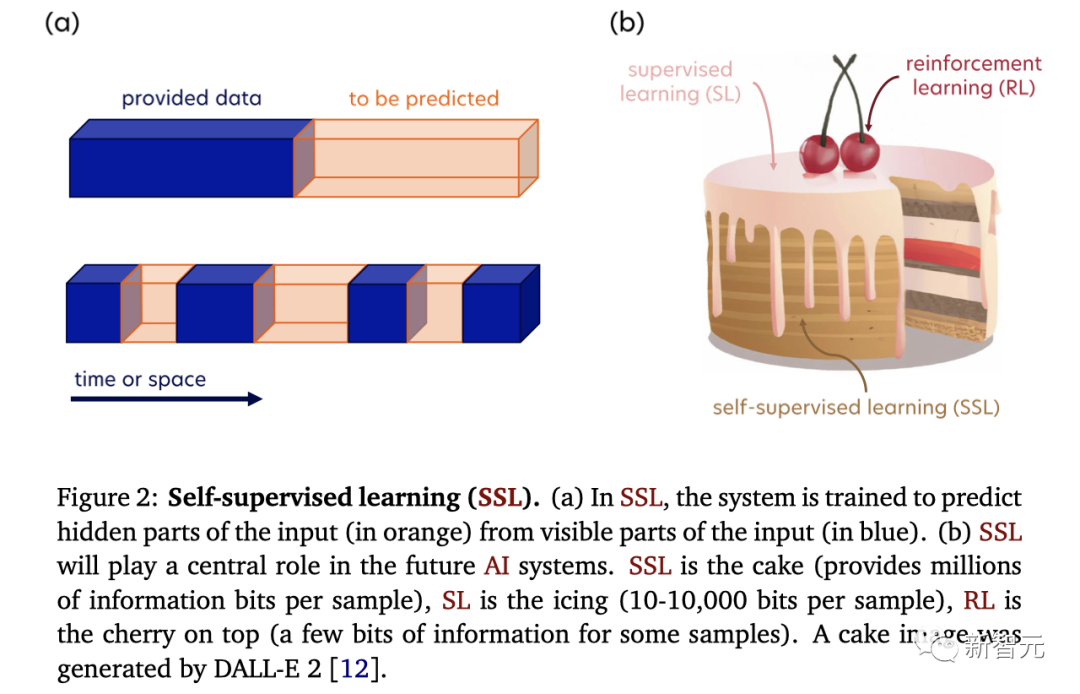
a.在SSL中,系统经过训练,可以从输入的可见部分(蓝色)预测输入的隐藏部分(橙色)。b. SSL将在未来的AI系统中发挥核心作用,SSL是蛋糕,SL是糖衣,RL是樱桃
模型中的「感知-计划-行动循环」类似于最优控制中的model-predictive control(MPC)。关键的区别在于,世界模型预测未来是通过学习。
它也不同于RL,因为在这里成本函数是已知的,所有模块都是可微的,在现实中不需要采取行动。
自监督学习与不确定性表征
自监督学习的主要目的,就是重建输入或预测输入的缺失部分,如上图a所示。
输入可以是图像、视频或文本。在训练中,模型学习数据的分层表征,因此,SSL的预训练通常先于SL或RL阶段。
它还用于学习预测(前向)模型MPC,或者学习控制策略,或基于模型的RL。
自监督学习对于文本非常有效,但对于图像来说,当模型被训练进行单一预测时,训练使它们预测的是所有可能的平均值,因此,SSL产生了模糊的预测。
不过,做决定通常不需要预测世界上所有可能的细节,只需要预测与任务相关的细节即可。


基于能量的模型
概率模型需要规范化,因此在高维数据的限制下,可能变得难以处理。
然而,在驾驶汽车的决策任务中,系统只需要选择正确的答案,其他答案的概率是无关紧要的。
因此,我们可以让模型通过能量函数来表示变量之间的依赖关系(例如下图a所示的决策y和条件x)。
在这种情况下,能量指导模型只需要将最低的能量分配给正确的答案,将较大的能量分配给不正确的答案即可。
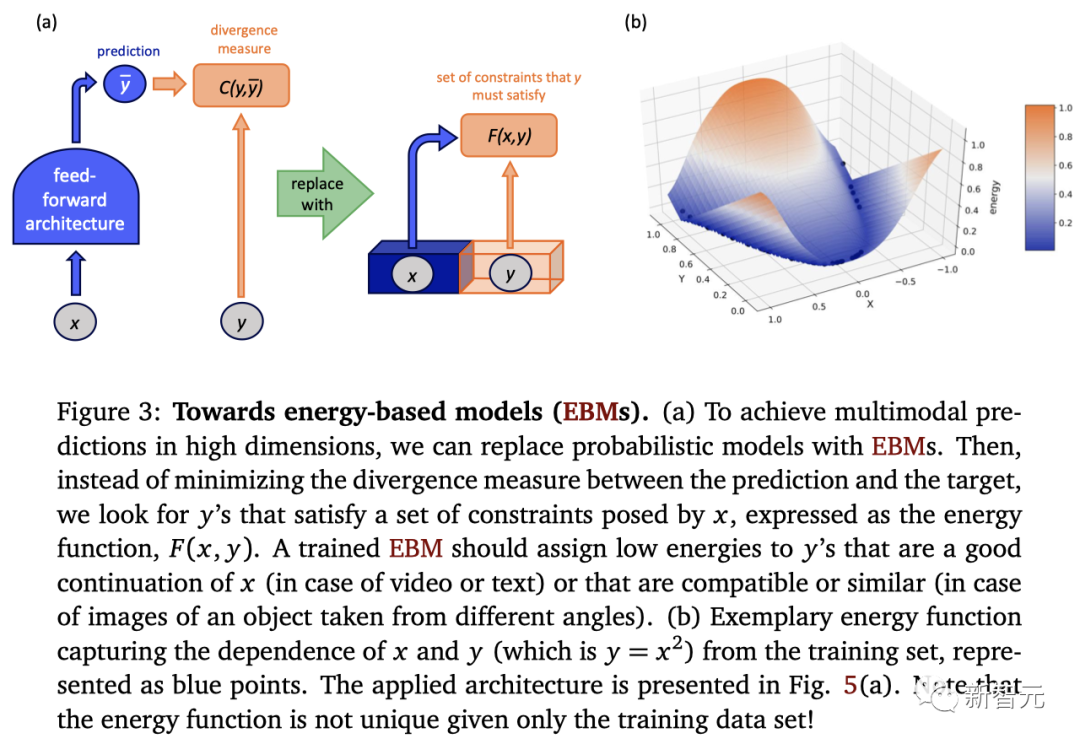
图b中的能量函数,表示了x和y之间的二次依赖关系。推理涉及为给定的x找到最小能量值。
EBM的一个优点是,可以表示多模态的依赖关系。理论上,还可以以各种形式(文本、视觉等)描述数据之间的依赖关系。


基于能量的模型与概率模型
在概率设置中,训练包括找到这样的模型参数w,使给定输入的观察输出的可能性最大(或负可能性最小)。
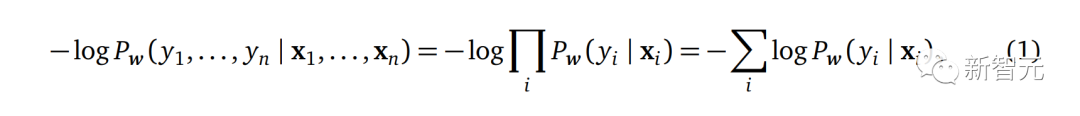
第一个等式是基于数据点之间相互独立的假设,而进行第二个变换,是因为求和计算比乘法计算更容易。
对于概率模型,训练仅限于从负对数似然(如交叉熵)生成的损失函数。
虽然放弃概率设置可能会令人惊讶,但请注意,做决策可以被视为选择得分最高的选项,而不是最有可能的选项。
比如在下棋的时候,如果查看所有可能性来决定下一步怎么走,显然非常棘手。
相反,可以通过探索可能性树的一部分,比如用蒙特卡洛树搜索的最短路径,给出最小能量。
因此,没有必要使用概率框架。
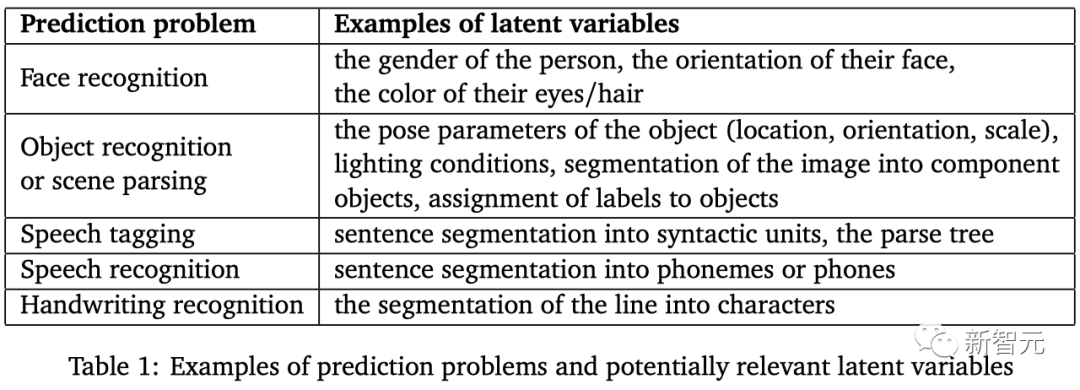
不过,如果需要的话,也可以通过将能量考虑为非归一化的负对数概率,在EBM和概率模型之间建立联系。
最常见的方法是通过Gibbs-Boltzmann distribution:
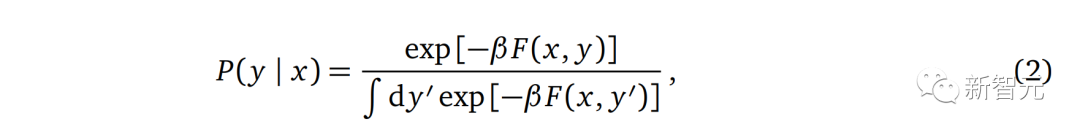
基于隐变量能量的模型
通过使用依赖于一组潜变量z的额外能量函数,我们可以扩展EBM的可能性。
这些隐藏变量通常被称为潜变量(latent variables),旨在捕捉在x中无法直接获得的y的信息。

在人脸检测任务中,这些潜变量的示例可能是性别、姿势或发色。
在自动驾驶汽车的情况下,潜变量可以参数化其他驾驶者的可能行为。
因此,它们为我们处理现实世界的不确定性提供了一种方法。

在结构化预测问题中,我们假设数据具有一些未知的结构,学习器必须解析这些结构才能进行准确的预测
最后,潜变量在所谓的结构化预测问题中非常有用。
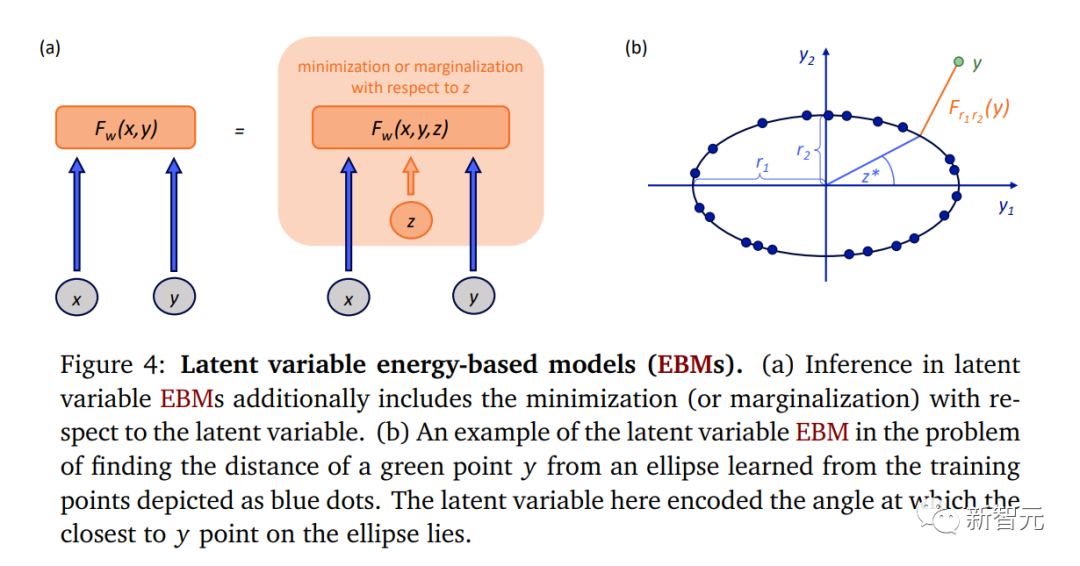
a.潜变量推断EBM还包括潜变量的最小化(或边缘化)。b. 一个潜变量EBM的例子,在寻找绿色点y和椭圆距离的问题中,它会从训练点(蓝点)学习
训练基于能量的模型
到目前为止,我们已经讨论了如何使用EBM,特别是潜变量EBM进行推理。
在本节中,我们将介绍如何训练EBM。

训练技术的选择,取决于EBM架构的选择。
让我们比较下图中的两种EBM架构。
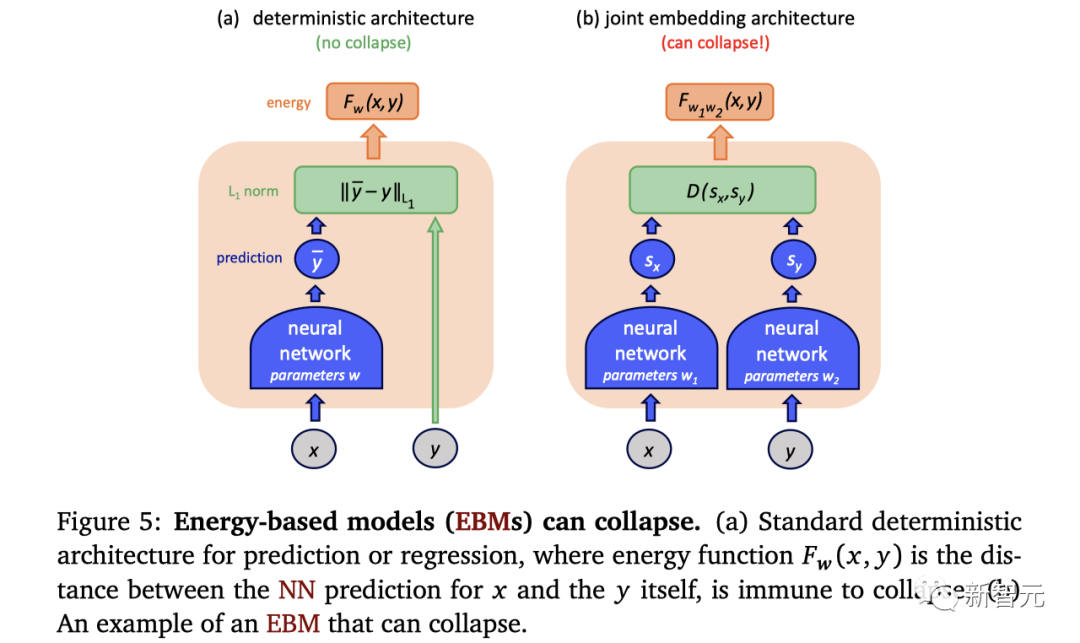
能量模型(EBM)可能会发生能量崩溃。(a)标准的确定性预测或回归架构,其中能量函数Fw(x, y)是x的神经网络预测与y本身之间的距离,不容易发生能量崩溃。(b)一个可能发生能量崩溃的EBM示例
在第一种情况下,能量函数只是数据点y和数据点x的编码器(如NN)输出之间的距离。
这种架构可以被认为是一个回归模型,并通过简单地最小化训练样本的能量来训练。
然而,对于其他架构,这样的训练可能会导致能量函数的崩溃,即给定一个x,能量(energy)可能会变得「平坦」,为 y 的所有值提供基本相同的能量。
例如,图b中的联合嵌入架构,将输入x和y分别编码为
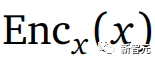
、
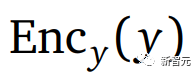
,目标是找到这样的
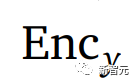
和
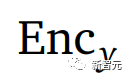
,这样它们的x和y的表示就是接近的。
如果我们训练模型只是为了最小化编码器输出之间的距离,那么两个编码器可能会完全忽略输入而只产生相同的恒定输出。
对比式方法
为了防止能量崩溃,我们可以采取对比式方法。
x和y是我们希望降低能量的训练数据点,在下图b中表示为蓝点。
ˆy是一个对比点,在下图b中表示为绿点,我们需要增加其能量。
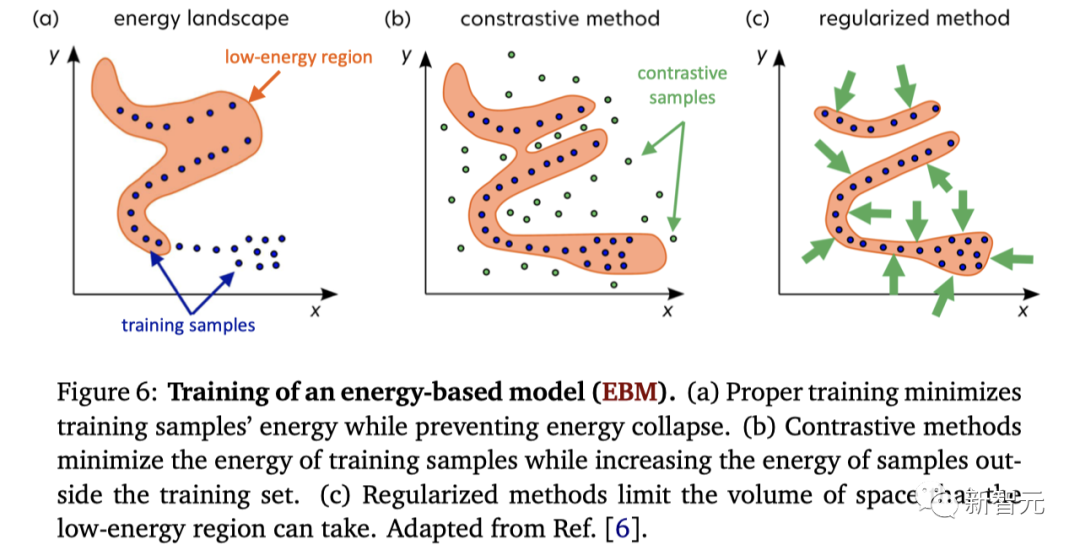
能量模型(EBM)的训练:(a) 正确的训练方式在最小化训练样本的能量的同时防止能量崩溃。(b) 对比式方法通过最小化训练样本的能量同时增加训练集之外样本的能量。(c) 正则化方法限制了低能量区域所占据的空间体积
当最小化
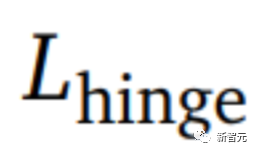
时,我们需要确保训练样本的能量雄安与训练样本和对比样本的能量,至少是边际m,这取决于y和ˆy之间的距离。
适当的对比损失函数需要确保非零边界,以避免能量崩溃。
对比损失函数可以像下面这个方程中的铰链损失,那样针对特定数据集进行成对计算。
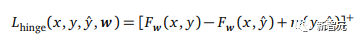
对比性方法最核心的问题是如何生成对比性点,然后最大可能性就可以被解释为对比方性方法的特例。
架构方法和正则化方法
我们的主要挑战在于,选择如何限制低能量空间的体积。
一种方法是构建低能量空间体积受限的体系结构。
另一种方法是添加一个正则化项,该项最小化低能量空间的某种度量。
最后,评分匹配(score matching)是一种正则化技术,它最小化数据点周围能量景观的梯度并最大化曲率。
几个能量模型的实例
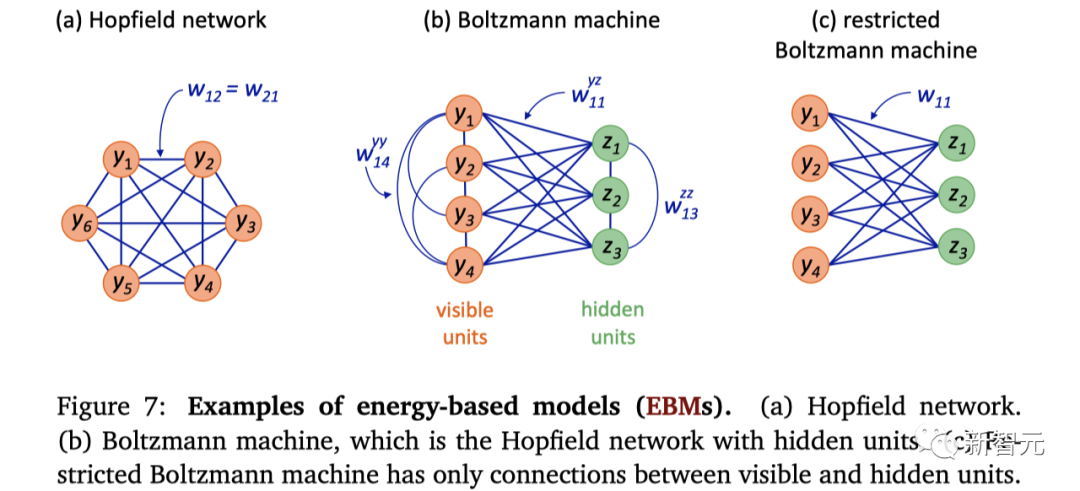
Hopfield网络
Hopfield网络网络是由John Hopfield在1982年推广的全连接循环网络,方案如图a所示,能量函数如下:
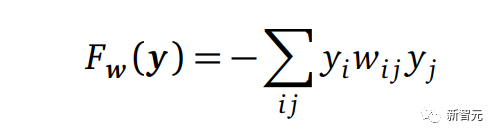
但是因为它会出现虚假最小值,使得在实践中可用性不强。
玻尔兹曼机
在1983年,由Geoffrey Hinton和Terrence Sejnowski提出了Hopfield网络的扩展,称为玻尔兹曼机。
它引入了被称为隐藏单元的神经元,如下图7(b)所示。
它的能量函数及其自由能如下:
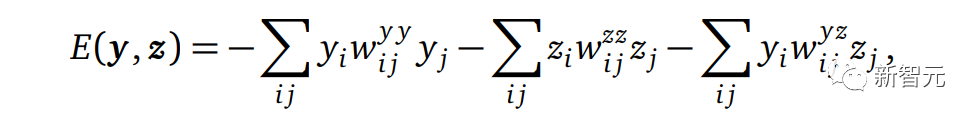
这个提议对整个机器学习社区来说非常重要,因为它首次引入了隐藏单元的概念,即那些输入和输出不可观测的神经元。
这些隐藏单元也可以理解为模型的潜变量。
去噪自编码器
去噪自编码器(Denoising Autoencoder,AE)是一种对比式EBM。
它是一种经过训练的自编码器,用于恢复被损坏输入的干净版本。
其架构示意图如下图8(a)所示。
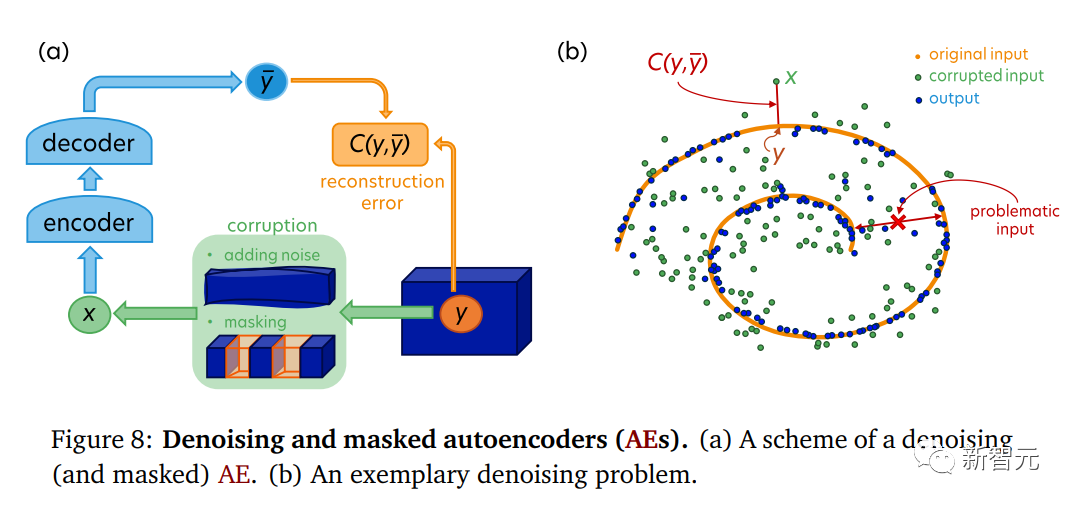
例如,该自编码器可以经过训练,使数据点在添加随机噪声后恢复到其原始位置,如图8(b)所示。
原始数据点来自橙色螺旋线,并通过在其位置上添加一些噪声进行损坏。
然后,将损坏的绿色数据点作为x输入到下图8(a)中的去噪自编码器,同时提供其干净版本y。
重构误差是损坏点与原始点之间的距离,当最小化时,去噪自编码器输出的蓝色数据点将回到螺旋线上。
需要注意的是,在同一个问题中,也存在对于去噪自编码器可能无法处理的问题点。例如,自编码器无法重构位于螺旋线两个分支之间、与它们等距离的数据点。
这个问题是由数据的折叠结构导致的,然而,在真实世界的数据中很少出现这种情况。
未来自主系统的构建模块
在上文中,我们看到了EBM如何克服概率模型的局限性之后,并且对于高维数据,可能应该使用正则化方法而不是对比式方法来训练它们。
讨论了潜变量模型并解释了它们在结构化预测问题或融入不确定性方面的用途之后,可以这些优势结合到一种称为联合嵌入预测架构(JEPA)的架构中。
这就是昨天Meta发布的I-JEPA模型的原理。
联合嵌入预测架构
联合嵌入预测架构(JEPA)是一种将嵌入模块与潜变量结合的EBM,如图9所示。
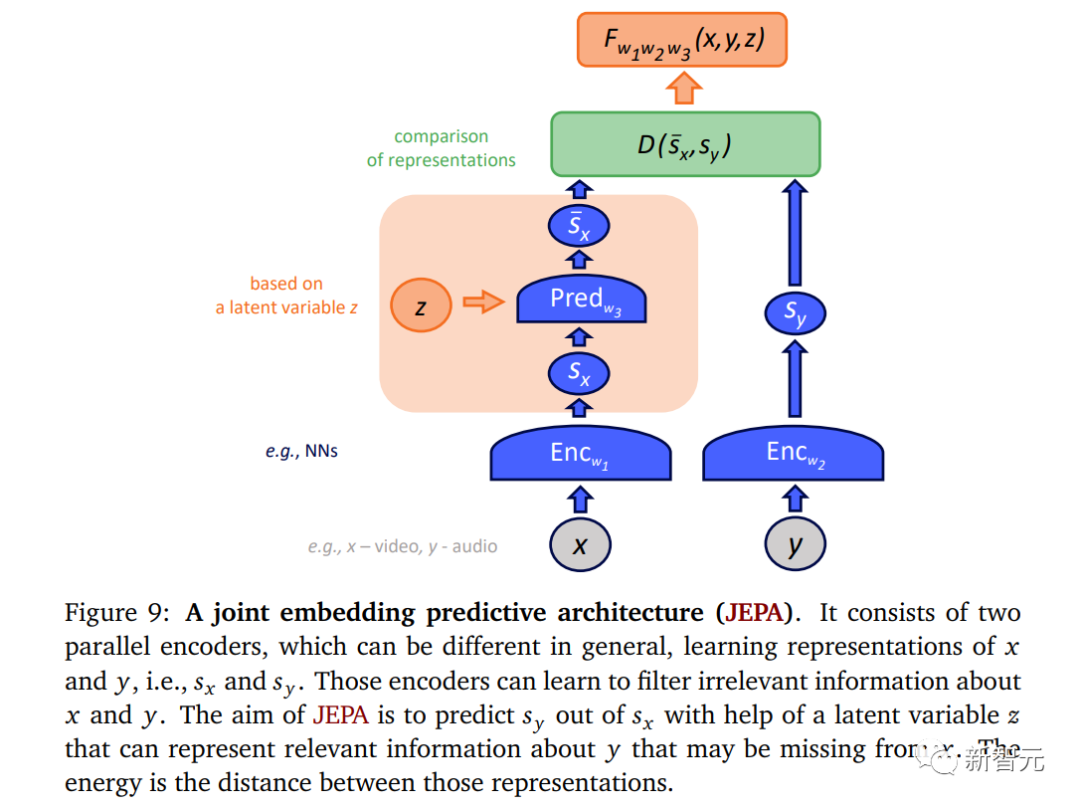
作为一个EBM,JEPA学习输入数据x和y之间的依赖关系,但是在学习的内部表示Sx和Sy的层次上进行比较,其中si = Enc(i)。
产生表示sx和sy的两个编码器可以不同,特别是具有不同的架构,并且不共享参数。
由于这一点,输入数据可以具有各种格式(例如视频和音频)。
此外,JEPA自然地处理多模态数据。
首先,x和y的编码器可以具有不变性特性,例如,将各种y映射到相同的Sy。
训练JEPA的最终目标是使表示Sx和Sy可以相互预测。
如我们在第4节中讨论的,EBM可以使用对比式方法和正则化方法进行训练,但对比式方法在高维情况下往往效率非常低下。
因此,JEPA可以使用损失函数进行训练,该损失函数除了包括预测误差外,还包括如下图10所示的正则化项。
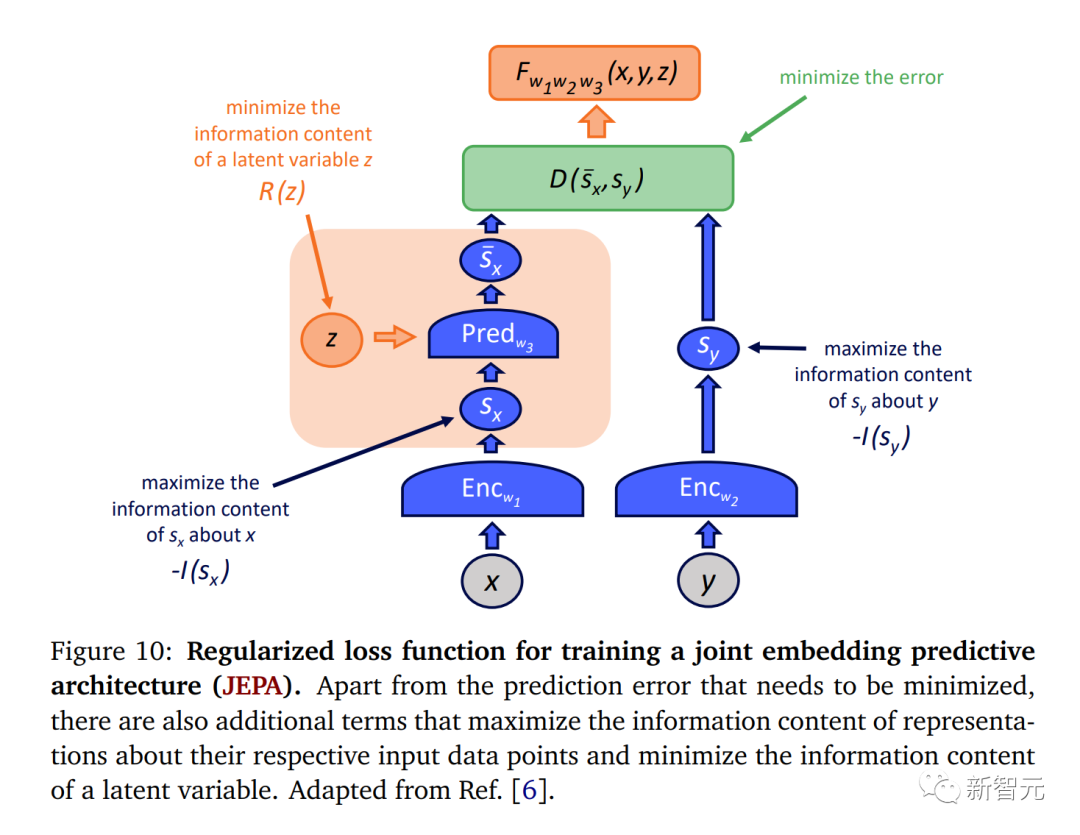
特别是为了防止信息能量崩溃,我们需要确保sx和sy尽可能多地携带关于x和y的信息。
否则,训练过程可能会导致编码器成为常数。
最后,我们需要最小化或限制潜变量的信息内容,以防止模型仅仅依赖于其中的信息。
结论
在笔记中,我们总结了LeCun的主要观点,解决了上边提到的AI现在发展中的局限性。
在第3节中,我们解释了由于现实世界的数据(如视频或文本)通常具有高维度,基于能量模型的发展方向(EBM)可能是比概率模型更有前景的发展方向。
在第4节中,我们介绍了对训练EBM的对比和正则化方法,并解释了由于在高维度中生成对比样本的成本巨大,正则化方法似乎更有前景用于训练未来的EBM。
在第5节中,我们给出了EBM的历史和现实的实际用例。
最后,第6节集中讨论了这个事实:人类决策过程基于各种格式和模态的数据,其结构通常需要解码才能进行预测,而且还包含可能是多余的信息。
这种多模态的障碍可以通过LeCun提出的一种新架构,在3个维度解决,这种构架被称为联合嵌入预测架构(JEPAs)。
最终,我们将要面对的挑战是使未来的自主AI能够对各种时间尺度和抽象级别上的世界状态进行预测。这种多层次的预测可以通过分层联合嵌入预测架构(H-JEPA)来实现。
通过正则化方法训练的这种架构,可能是设计能够在不确定性下的预测世界模型的起点,这将成为未来自主AI发展中取得突破。










































