大规模语言模型虽然在各大自然语言处理任务上都展现了优越的性能,不过算术类题目仍然是一大难关,即便是当下最强的GPT-4也很难处理基础运算的问题。
最近,来自新加坡国立大学的研究人员提出了一个专供算术的模型山羊Goat,在LLaMA模型基础上微调后,实现了显著优于GPT-4的算术能力。

论文链接:https://arxiv.org/pdf/2305.14201.pdf
通过对合成的算术数据集进行微调,Goat在BIG-bench算术子任务上实现了最先进的性能,
Goat仅通过监督微调就可以在大数加减运算上实现近乎完美的准确率,超越了之前所有的预训练语言模型,如Bloom、OPT、GPT-NeoX等,其中零样本的Goat-7B所达到的精度甚至超过了少样本学习后的PaLM-540
研究人员将Goat的卓越性能归功于LLaMA对数字的一致性分词技术。
为了解决更有挑战性的任务,如大数乘法和除法,研究人员还提出了一种方法,根据算术的可学习性对任务进行分类,然后利用基本的算术原理将不可学习的任务(如多位数乘法和除法)分解为一系列可学习的任务。
通过全面的实验验证后,文中提出的分解步骤可以有效地提升算术性能。
并且Goat-7 B可以在24 GB VRAM GPU上使用LoRA高效训练,其他研究人员可以非常容易地重复该实验,模型、数据集和生成数据集的python脚本即将开源。
会算数的语言模型
语言模型
LLaMA是一组开源的预训练语言模型,使用公开可用的数据集在数万亿个token上进行训练后得到,并在多个基准测试上实现了最先进的性能。
先前的研究结果表明,分词(tokenization)对LLM的算术能力很重要,不过常用的分词技术无法很好地表示数字,比如位数过多的数字可能会被切分。
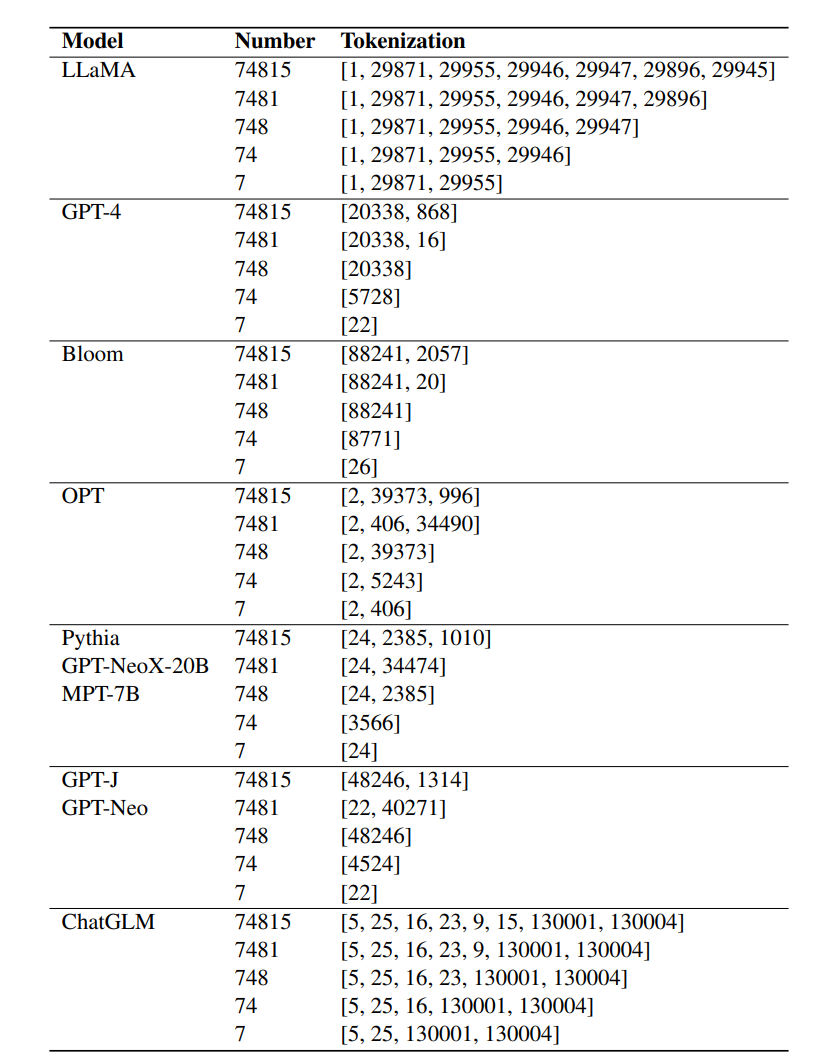
LLaMA选择将数字切分为多个token,确保数字表示的一致性,研究人员认为,实验结果中表现出的非凡算术能力主要归功于LLaMA对数字的一致性分词。
在实验中,其他微调后的语言模型,如Bloom、OPT、GPT-NeoX和Pythia,无法与LLaMA的算术能力相匹配。
算术任务的可学习性(Learnability of Arithmetic Tasks)
之前有研究人员对使用中间监督解决复合任务(composite task)进行了理论分析,结果表明这种任务是不可学习的,但可以分解为多项式数量的简单子任务。
也就是说,不可学习的复合问题可以通过使用中间监督或逐步思维链(CoT)来学习。
在此分析基础上,研究人员首先对可学习和不可学习任务进行实验分类。
在算术计算的背景下,可学习任务通常是指那些可以成功训练模型以直接生成答案的任务,从而在预定义数量的训练epochs内实现足够高的精度。
不可学习的任务是那些即使经过广泛训练,模型也难以正确学习和生成直接答案的任务。
虽然任务可学习性变化背后的确切原因尚不完全清楚,但可以假设这与基本模式的复杂性和完成任务所需的工作记忆大小有关。
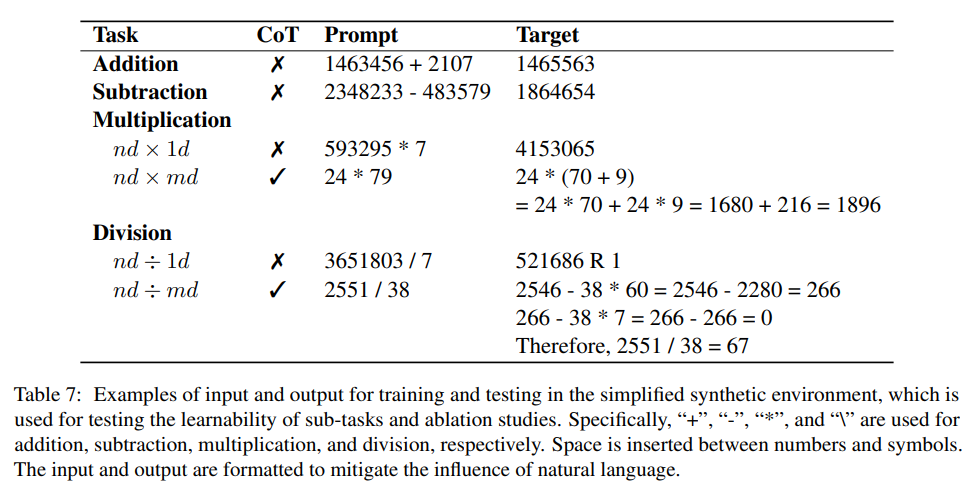
研究人员通过在简化的合成环境中专门针对每个任务微调模型来实验检查这些任务的可学习性。
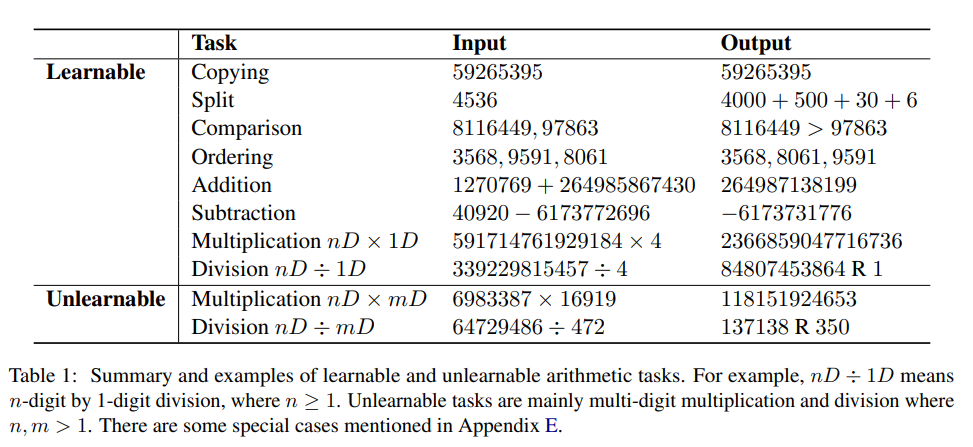
可学习的和不可学习的任务
任务分类的结果也与人类的感知相同,通过实践,人类可以在脑海中计算两个大数字的加法和减法,无需手算的情况下,可以直接从左(最高有效数字)到右(最低有效数字)写下最终的数字答案。
不过心算解决大数乘法和除法是一项具有挑战性的任务。
还可以观察到,上述对任务的分类结果与GPT-4的性能也一致,特别是GPT-4擅长为大数加法和减法生成直接答案,当涉及到多位乘法和除法任务时,准确性会显著下降。
像GPT-4这样强大的模型无法直接解决不可学习的任务,也可能表明,即使经过广泛的训练,为这些任务生成直接答案也是极具挑战性的。
值得注意的是,对于LLaMA来说是可学习的任务可能不一定对于其他LLM来说是可学的。
此外,并非所有被归类为不可学习的任务对模型来说都是完全不可能学习到的。
例如,两位数乘两位数被认为是一项不可学习的任务,但如果训练集中包含所有可能的2位数乘法枚举数据的话,模型仍然可以通过过拟合训练集来直接生成答案。
不过整个过程需要近10个epoch才能达到90%左右的准确率。
而通过在最终答案之前插入文中提出的CoT,该模型可以在1个epoch的训练后就可以在两位数乘法中实现相当不错的精度,也与之前的研究结论一致,即中间监督的存在有助于学习过程。
加法与减法
这两个算术操作是可学习的,仅通过有监督微调,模型就表现出了准确生成直接数字答案的非凡能力。
尽管模型只是在非常有限的加法数据子集上进行了训练,但从模型在未见过的测试集上实现了近乎完美的准确率上可以看出来,模型成功地捕获了算术运算的基本模式,并且无需使用CoT
乘法
研究人员通过实验验证了n位数乘1位数的乘法是可学习的,而多位数乘法则无法学习。
为了克服这个问题,研究人员选择在生成答案之前对LLM进行微调以生成CoT,将多位数乘法分解为5个可学习的子任务:
1. 抽取(extraction),从自然语言指令中抽取算术表达式
2. 拆分(split),将两者中较小的数拆分为place值
3. 展开(expansion),基于分配性展开求和
4. 乘积(product),同时计算每个乘积
5. 逐项相加(adding term by term),将前两项相加,复制其余项,得到最终和

其中每个任务都是可学习的。
除法
类似地,可以通过实验观察到n位数除以1位数是可以学习的,而多位数除法是不可学习的。
研究人员利用改进慢除法的递推方程,设计了一个全新的思维链提示。
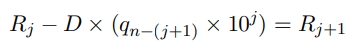
主要思想是从被除数中减去除数的倍数,直到余数小于除数。
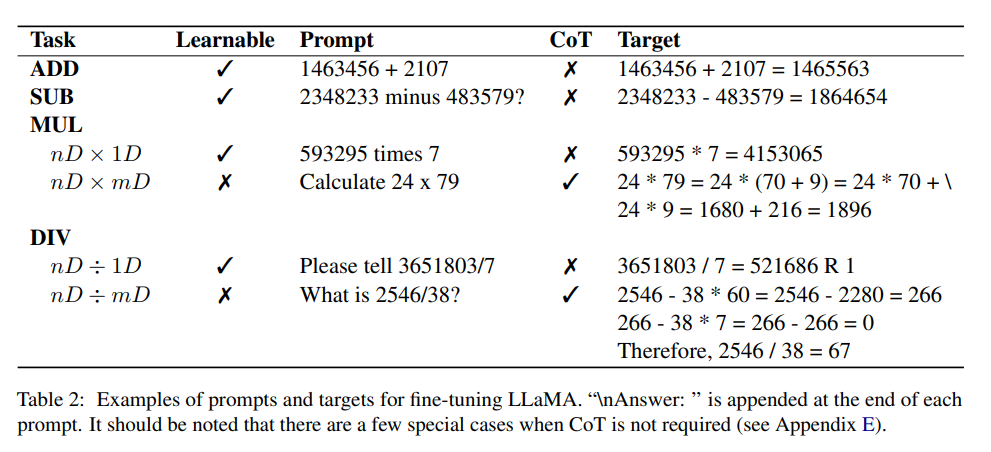
数据集
文章中设计的实验为两个正整数的加法和减法,每个正整数最多包含16位数字,并且减法运算的结果可能是负数。
为了限制生成的最大序列长度,乘法的结果为12位以内的正整数;两个正整数的除法中,被除数小于12位,商值6位数以内。
研究人员使用Python脚本合成了一个数据集,生成了大约100万个问答对,答案包含提出的CoT以及最终的数字输出,所有数字都是随机生成的,可以保证重复实例的概率非常低,不过小数字可能会被多次采样。
微调
为了使该模型能够基于指令解决算术问题,并促进自然语言问答,研究人员使用ChatGPT生成了数百个指令模板。
在指令调整过程中,从训练集中为每个算术输入随机选择一个模板,并微调LLaMA-7B,类似于Alpaca中使用的方法。

Goat-7B可以在24GB VRAM GPU上使用LoRA进行微调,在A100 GPU上仅花费大约1.5小时即可完成10万样本的微调,并实现近乎完美的精度。
实验结果
比较Goat和GPT-4在大量乘法和除法方面的性能似乎不公平,因为GPT-4会直接生成答案,而Goat则依赖于设计的思维链,所以在GPT-4评估时还在每个提示的结尾加入「Solve it step by step」
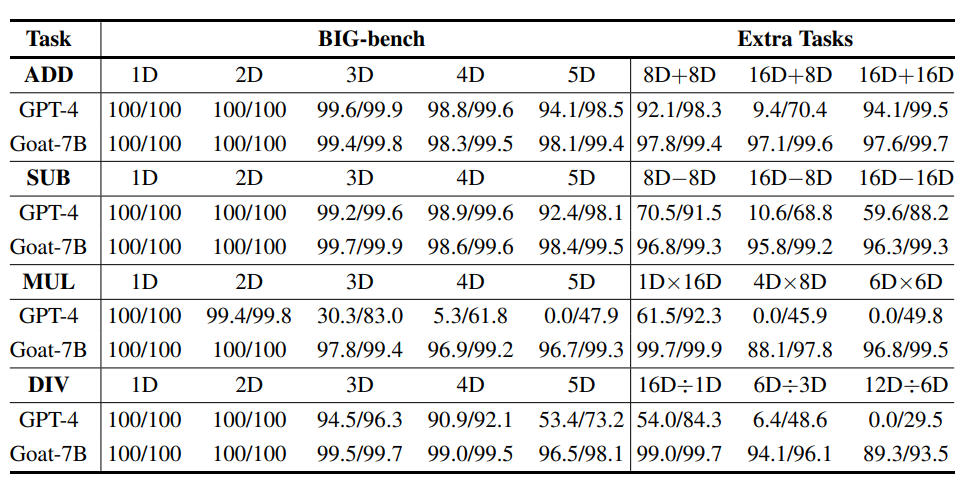
不过可以观察到,虽然GPT-4在某些情况下,长乘法和除法的中间步骤错了,但最终答案仍然是正确的,也就意味着GPT-4并没有利用思维链的中间监督来提高最终输出。
最终从GPT-4的解决方案中确定了以下3个常见错误:
1. 对应数字的对齐
2. 重复数字
3. n位数乘以1位数的中间结果错误
从实验结果中可以看插到,GPT-4在8D+8D和16D+16D任务上表现相当好,但在大多数16D+8D任务上的计算结果都是错误的,尽管直观上来看,16D+8D应该比16D+16D相对容易。
虽然造成这种情况的确切原因尚不清楚,但一个可能的因素可能是GPT-4不一致的数字分词过程,使得两个数字之间很难对齐.








































