
今天是十五周算法训练营的第十周,主要讲回溯算法专题。
解决一个回溯问题,实际上就是一个决策树的遍历过程,只需要思考三个问题:
- 路径:也就是已经做出的选择
- 选择列表:也就是你当前可以做的选择
- 结束条件:也就是到达决策树底层,无法再做选择的条件
全排列
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以按任意顺序 返回答案。
示例 1:
输入:nums = [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]。
function permute(nums) {
const result = [];
/**
* 路径:记录到track中
* 选择列表:不存在与nums中的哪些数
* 结束条件:当nums中的元素全部在track中出现
*/
const backtrack = (track, nums) => {
// 结束条件
if (track.length === nums.length) {
result.push([...track]);
return;
}
for (let i = 0; i < nums.length; i++) {
if (track.includes(nums[i])) {
continue;
}
// 做选择
track.push(nums[i]);
// 进入下一层
backtrack(track, nums);
// 取消选择
track.pop();
}
};
const track = [];
backtrack(track, nums);
return result;
}
const nums = [1, 2, 3];
console.log(permute(nums));全排列II
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
示例 1:
输入:nums = [1,1,2] 输出: [[1,1,2], [1,2,1], [2,1,1]]。
function permuteUnique(nums) {
const result = [];
/**
* 路径:记录到track中
* 选择列表:当前没有被访问过,且前一个值若为相通知,且被访问过
* 结束条件:全部值都被访问了一遍
*/
const backtrack = (sortNums, track, visits) => {
if (track.length === sortNums.length) {
result.push([...track]);
return;
}
for (let i = 0; i < sortNums.length; i++) {
// i > 0 && nums[i] === nums[i - 1] && !visits[i - 1]
// 上述一行的判断是当前值和前一个值相等,但是前一个值没有被访问过,表示前一个值不在该值路径的上几层,表示在同一层前面出现过,所以该值要跳过
if (visits[i] || (i > 0 && sortNums[i] === sortNums[i - 1] && !visits[i - 1])) {
continue;
}
// 做选择
track.push(sortNums[i]);
visits[i] = 1;
// 选择下一层
backtrack(sortNums, track, visits);
// 取消选择
track.pop();
visits[i] = 0;
}
};
const track = [];
nums.sort((a, b) => a - b);
const visits = (new Array(nums.length)).fill(0);
backtrack(nums, track, visits);
return result;
}
const nums = [1, 1, 2];
console.log(permuteUnique(nums));N皇后
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例 1:
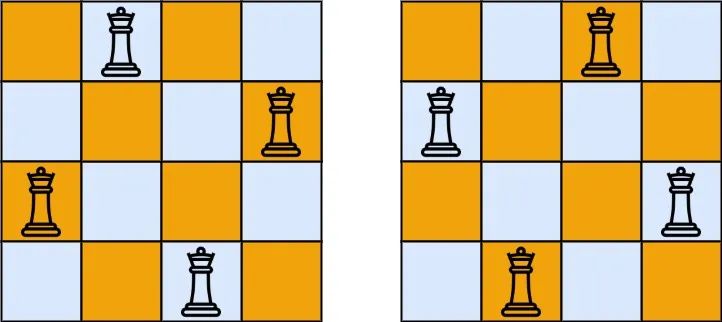
输入:n = 4 输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]] 解释:如上图所示,4 皇后问题存在两个不同的解法。
// 该问题本质上和全排列问题差不多,决策树上的每一层表示棋盘上的每一行,每个节点可以做出的选择是在该行的任意一列放置一个皇后
function solveNQueens(n) {
const result = [];
// 判断是否可以在[row, col]放置皇后
const isValid = (board, row, col) => {
// 判断该列是否存在皇后
for (let i = 0; i < row; i++) {
if (board[i][col] === 'Q') {
return false;
}
}
// 判断左上方是否存在皇后冲突
let leftRow = row - 1;
let leftCol = col - 1;
while (leftRow >= 0 && leftCol >= 0) {
if (board[leftRow][leftCol] === 'Q') {
return false;
}
leftRow--;
leftCol--;
}
// 判断右上是否存在皇后冲突
let rightRow = row - 1;
let rightCol = col + 1;
while (rightRow >= 0 && rightCol < n) {
if (board[rightRow][rightCol] === 'Q') {
return false;
}
rightRow--;
rightCol++;
}
return true;
};
/**
* 路径:board中小于row的那些行都已经成功放置了皇后
* 选择列表:第row行的所有列都是放置皇后的选择
* 结束条件:row超过board的最后一行
*/
const backtrack = (board, row) => {
// 触发结束条件
if (row === board.length) {
result.push(board.map(item => {
return item.join('');
}));
return;
}
for (let col = 0; col < n; col++) {
// 排除不合法的选择
if (!isValid(board, row, col)) {
continue;
}
// 做选择
board[row][col] = 'Q';
// 进行下一层
backtrack(board, row + 1);
// 取消选择
board[row][col] = '.';
}
};
const board = new Array(n);
for (let i = 0; i < n; i++) {
board[i] = (new Array(n)).fill('.');
}
backtrack(board, 0);
return result;
}
const n = 4;
console.log(solveNQueens(n));组合总和
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
示例 1:
输入:candidates = [2,3,6,7], target = 7 输出:[[2,2,3],[7]] 解释: 2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。 7 也是一个候选, 7 = 7 。 仅有这两种组合。
function combinationSum(candidates, target) {
const result = [];
/**
* 路径:记录在track中
* 选择列表:index及其之后的元素
* 结束条件:其和为target,则进行存储,超过,则不存储结束
*/
const backtrack = (sortNums, track, trackNum, index) => {
if (trackNum === target) {
result.push([...track]);
return;
} else if (trackNum > target) {
return;
}
for (let i = index; i < sortNums.length; i++) {
// 做选择
track.push(sortNums[i]);
trackNum += sortNums[i];
// 进入下一层
backtrack(sortNums, track, trackNum, i);
// 取消选择
track.pop();
trackNum -= sortNums[i];
}
};
const track = [];
let trackNum = 0;
candidates.sort((a, b) => a - b);
backtrack(candidates, track, trackNum, 0);
return result;
}
const candidates = [2,3,6,7];
const target = 7;
console.log(combinationSum(candidates, target));子集II
给你一个整数数组 nums ,其中可能包含重复元素,请你返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。返回的解集中,子集可以按 任意顺序 排列。
示例 1:
输入:nums = [1,2,2] 输出:[[],[1],[1,2],[1,2,2],[2],[2,2]]。
function subsetsWithDup(nums) {
const result = [];
/**
* 路径:记录在track中
* 选择列表:index及其之后的元素
* 结束条件:将结果进行存储
*/
const backtrack = (sortNums, track = [], index = 0) => {
result.push([...track]);
for (let i = index; i < sortNums.length; i++) {
// 对于排序后相同的元素应该跳过
if (i > index && sortNums[i] === sortNums[i - 1]) {
continue;
}
// 做选择
track.push(sortNums[i]);
// 进入下一层
backtrack(sortNums, track, i + 1);
// 取消选择
track.pop();
}
};
const track = [];
nums.sort((a, b) => a - b);
backtrack(nums, track, 0);
return result;
}
const nums = [1, 2, 2];
console.log(subsetsWithDup(nums));递增子序列
给你一个整数数组 nums ,找出并返回所有该数组中不同的递增子序列,递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。
数组中可能含有重复元素,如出现两个整数相等,也可以视作递增序列的一种特殊情况。
示例 1:
输入:nums = [4,6,7,7] 输出:[[4,6],[4,6,7],[4,6,7,7],[4,7],[4,7,7],[6,7],[6,7,7],[7,7]]。
function findSubsequences(nums) {
const result = [];
const backtrack = (track, start) => {
// 如果其长度大于等于2,则算一个子序列
if (track.length >= 2) {
result.push([...track]);
}
const map = new Map();
for (let i = start; i < nums.length; i++) {
// 判断是否合法
// 同一层只能用一次
if (map.has(nums[i])) {
continue;
}
// 后一层比前一层大
if (nums[i] < track[track.length - 1]) {
continue;
}
map.set(nums[i], true);
// 做选择
track.push(nums[i]);
// 进入下一层
backtrack(track, i + 1);
// 取消选择
track.pop();
}
};
const track = [];
backtrack(track, 0);
return result;
}
const nums = [1, 2, 3 ,1,1,1,1];
console.log(findSubsequences(nums));






































