
一、因果推断的研究范式
研究范式目前主要有两个主要的研究方向:
- Judea Pearl Structure Model
- 潜在的输出框架
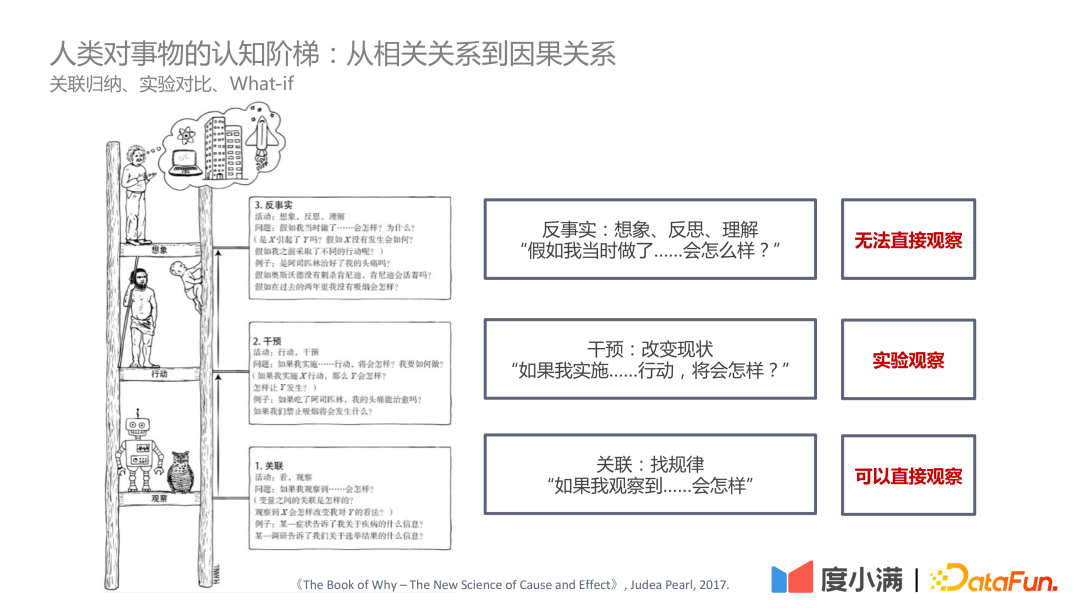
在Judea Pearl 《The Book of Why – The New Science of Cause and Effect》这本书中,将认知阶梯定位为三层:
- 第一层-关联:通过关联的方式找出规律,可以直接观察;
- 第二层-干预:如果改变现状,应当实施什么样的行动,得出什么样的结论,可以通过实验观察;
- 第三层-反事实:由于法律法规等问题无法直接实验观察,通过反事实假设,如果实施了行动,会发生什么,如何评估ATE和CATE,是较为困难的一个问题。
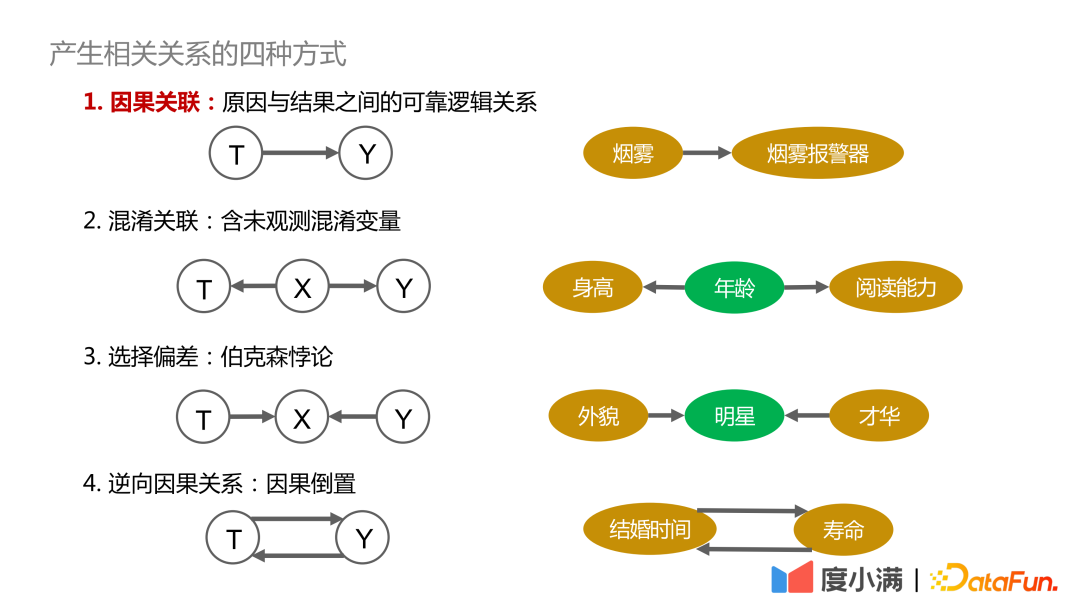
首先阐述下产生相关关系的四种方式:
1. 因果关联:原因和结果之间有可靠的,可追溯的,能够正向依赖的关系,比如烟雾与烟雾报警器具有因果关联;
2. 混淆关联:含有未能直接观测的混淆变量,比如身高和阅读能力是否能够关联起来,需要控制年龄这个变量相似,从而得出有效的结论;
3. 选择偏差:本质上是伯克森悖论,比如探究外貌和才华的关系,如果只在明星群体中观察,可能会得出结论:长相和才华不可兼得。如果在全部人类里观察,长相与才华没有因果关系。
4. 逆向因果关系:即因果倒置,比如统计显示人类结婚时间越长,寿命就越长。但是反过来,我们不能说:如果想获取更长的寿命,就要早早结婚。
混淆因子如何影响观测结果,这里有两个case可以说明:
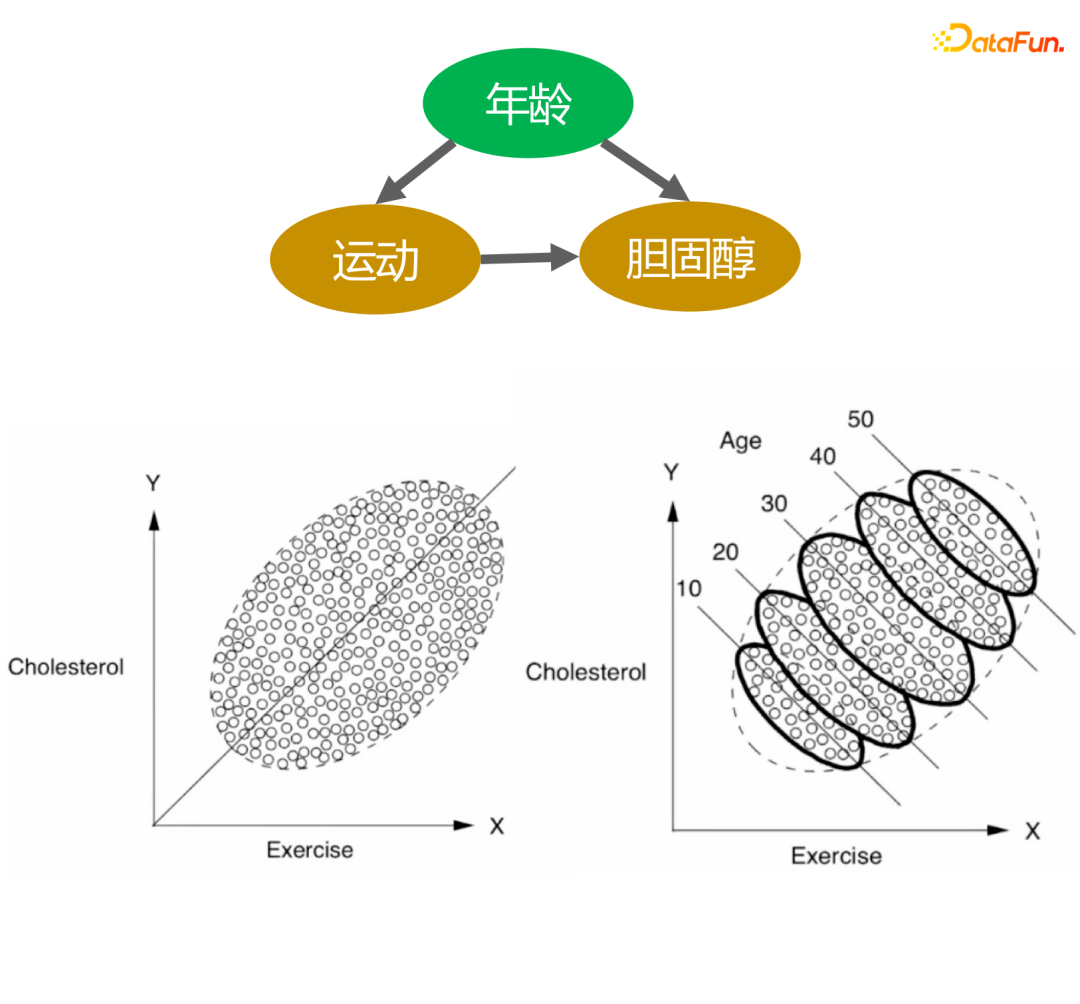
上面图片描述了运动量与胆固醇水平的关系。从左图可得出结论:运动量越大,胆固醇水平越高。但是加入年龄分层来看,相同年龄分层下,运动量越大,胆固醇水平越低。此外,随着年龄增长,胆固醇水平逐渐升高,这个结论才符合我们的认知。
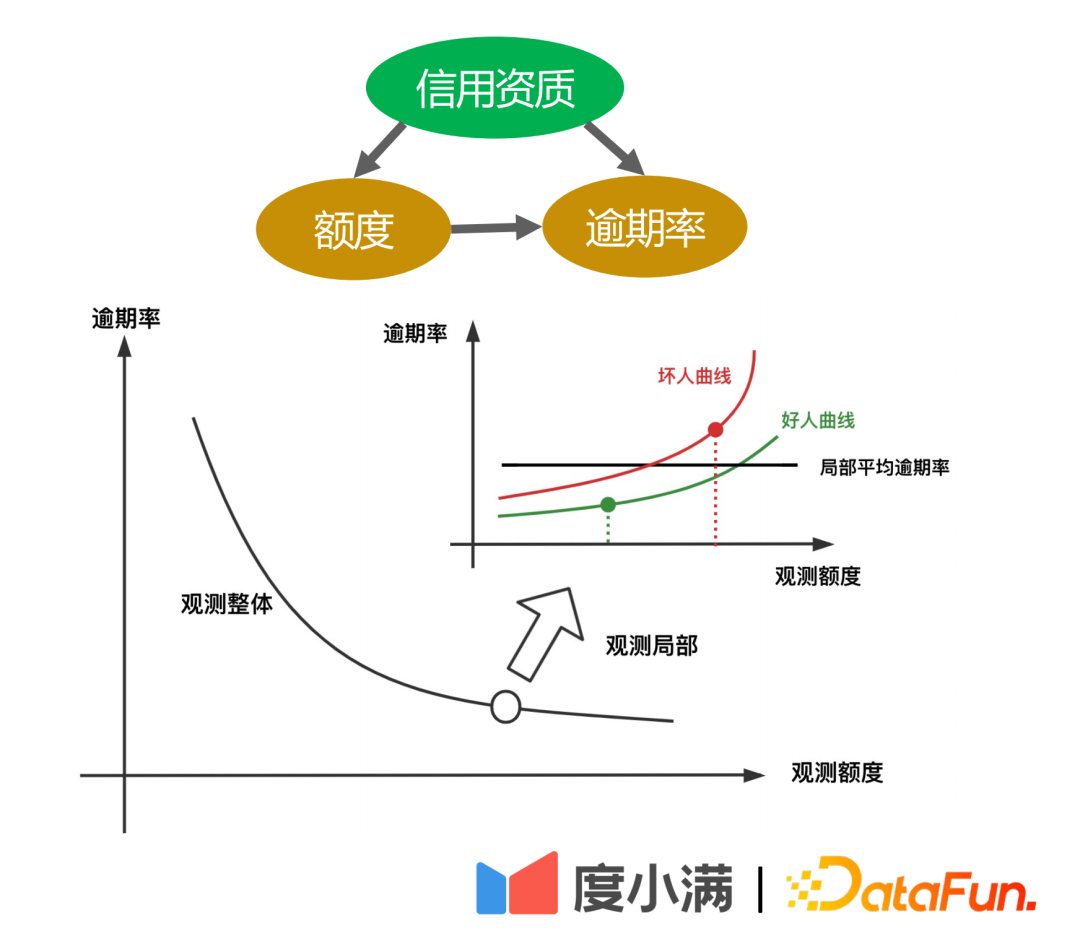
第二个例子为信贷场景。从历史统计数据中可以看出,给定的额度(能借到的钱款数)越高,逾期率越低。但是金融领域,会首先根据借款人的A卡判断其信用资质,如果信用资质越好,则平台赋予额度越高,整体逾期率也很低。但是根据局部随机实验表明,相同信用资质人群,会有一部分人其额度风险迁移曲线变化比较缓慢,也会有一部分人其额度迁移风险较高,即额度提升后,带来的风险增量较大。
上面两个case说明,如果建模中忽略混淆因子,可能会得到错误,甚至相反的结论。
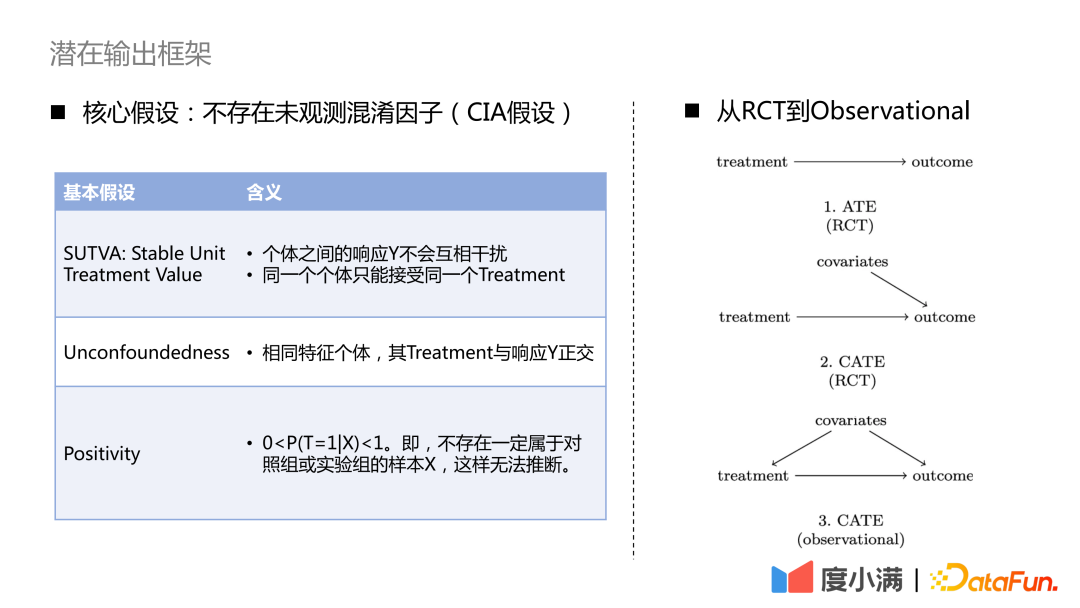
如何从RCT随机样本过渡到观测样本因果建模?
对于RCT样本的情况,如果希望评估ATE指标,可以通过分组相减或DID(difference in difference)。如果希望评估CATE指标,可以通过uplift 建模。常见的方法比如有meta-learner,double machine learning,causal forest等等。这里需要注意必要的三大假设:SUTVA,Unconfoundedness和Positivity。最核心的假设为:不存在未观测混淆因子。
对于仅有观测样本的情况,无法直接获取treatment->outcome的因果关系,我们需要借助必要的手段切断covariates到treatment的后门路径。常见方法是工具变量法和反事实表示学习。工具变量法需要对具体业务抽丝剥茧,绘制业务变量中因果图。反事实表示学习则依靠成熟的机器学习,匹配covariates相似的样本做因果评估。
二、、因果推断的框架演进
1、从随机数据到观测数据
接下来介绍因果推断的框架演进,是如何一步步过度到因果表示学习的。
常见Uplift Model有:Slearner, Tlearner, Xlearner。
其中Slearner将干预变量视为一维特征。需要注意,在常见的树模型里,treatment容易被淹没,导致treatment effect估计偏小。
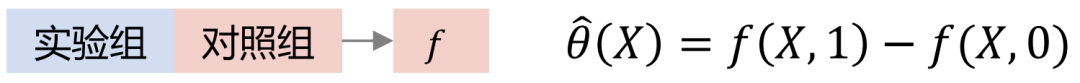
Tlearner将treatment离散化,对干预变量分组建模,每一个treatment建立预测模型,再作差。需要注意,较少的样本量会带来较高的估计方差。
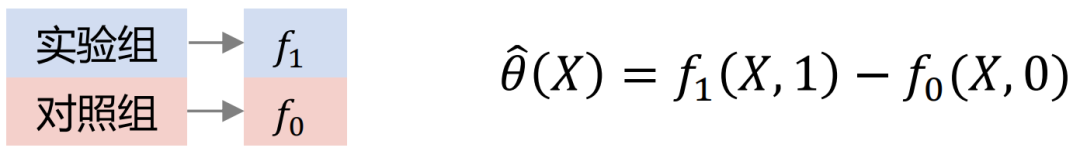
Xlearner分组交叉建模,将实验组和对照组分别进行交叉计算训练。该方法综合了S/T-learner的优点,其缺点是引入了更高的模型结构误差,提高了调参难度。
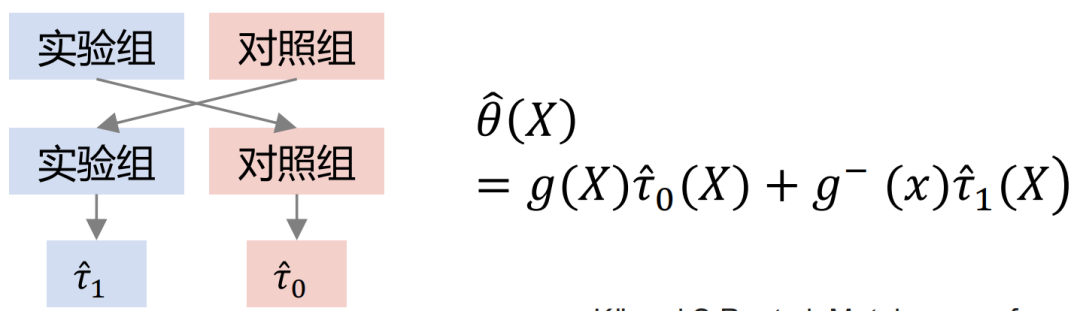
三种model比较:
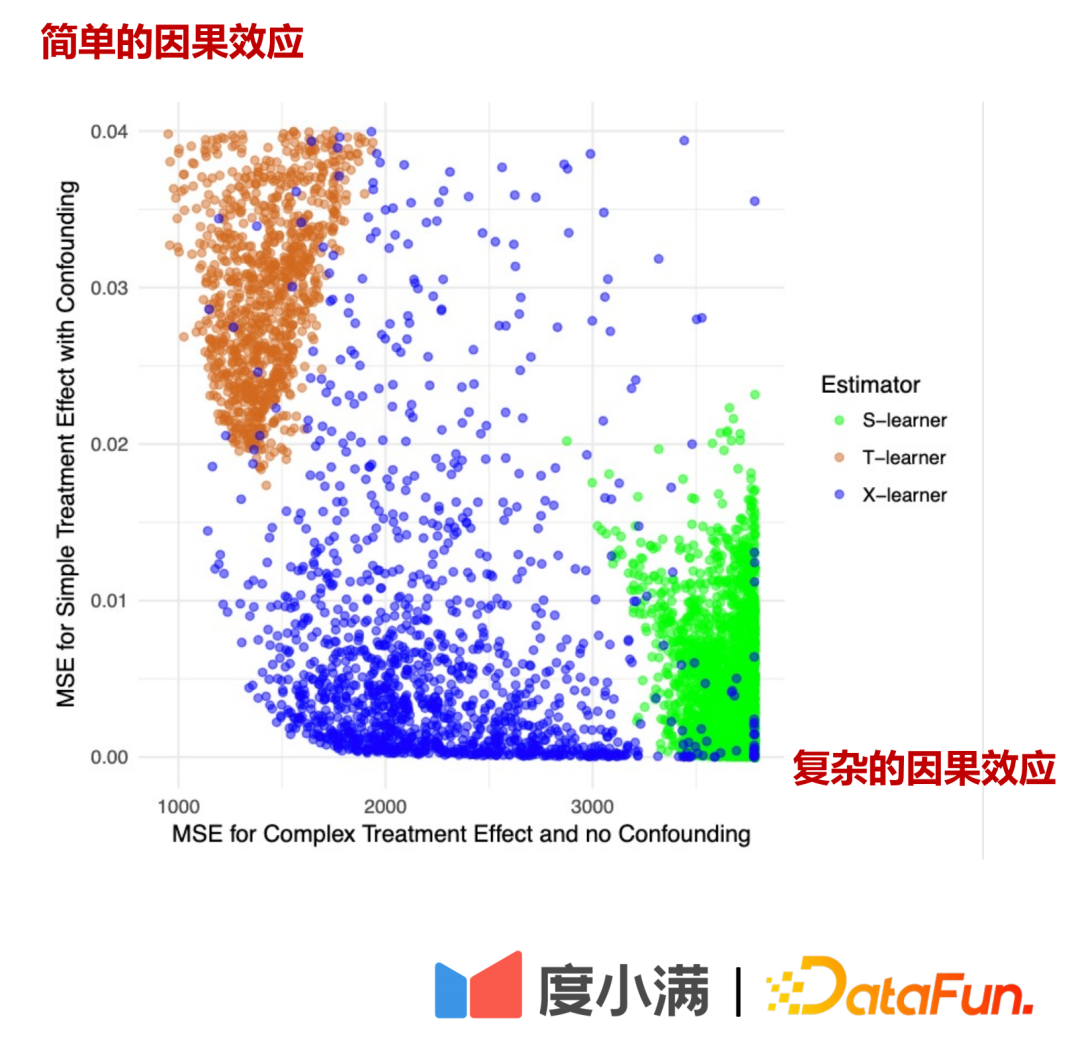
在上图中,横轴是复杂的因果效应,MSE的的估计误差,纵轴是简单的因果效应,横轴纵轴分别表示两份数据。绿色表示Slearner的误差分布,褐色表示Tlearner的误差分布,蓝色表示Xlearner的误差分布。
在随机样本条件下,Xlearner对于复杂的因果效应估计和简单的因果效应估计均更优;Slearner对于复杂因果效应预估表现相对较差,对简单因果效应估计更优;Tlearner则与Slearner相反。
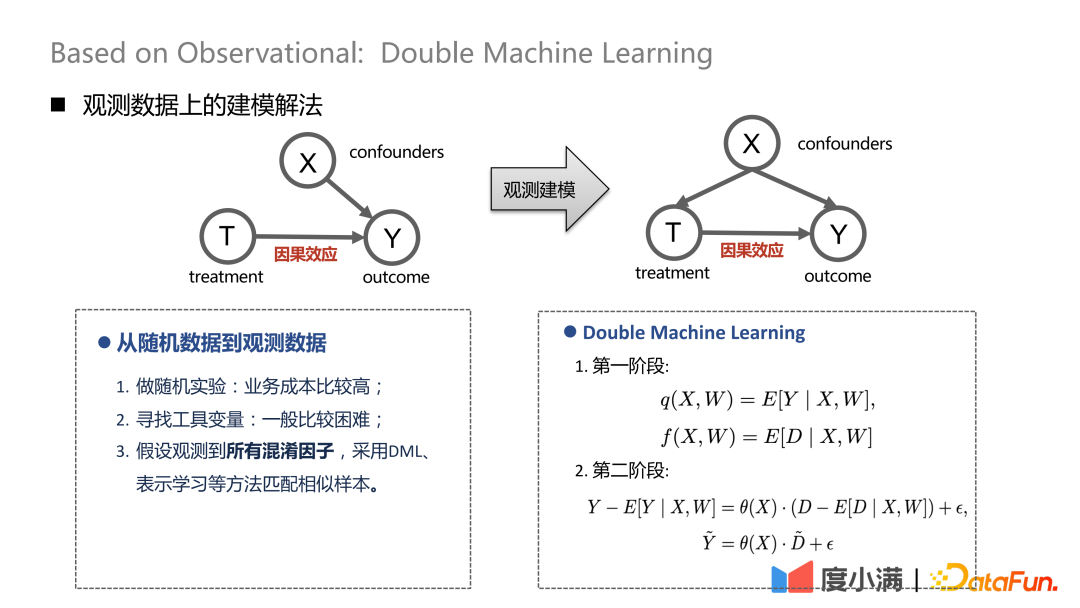
如果有随机样本,X到T的箭头可以去掉。过渡到观测建模后X到T的箭头去不掉,treatment和outcome会同时受到confounders的影响,这时可以进行一些消偏处理。比如DML(Double Machine Learning)的方式,进行两阶段建模。在第一阶段中,这里的X是用户自身的表征特征,比如年龄、性别等。混淆变量会包括比如历史中对筛选特定人群的操作。在第二阶段中,对上一阶段计算结果的误差进行建模,这里的即是对CATE的估计。
从随机数据到观测数据有三种处理方式:
(1)做随机试验,但业务成本较高;
(2)寻找工具变量,一般比较困难;
(3)假设观测到所有的混淆因子,利用DML、表示学习等方法匹配相似样本。
2、因果表示学习
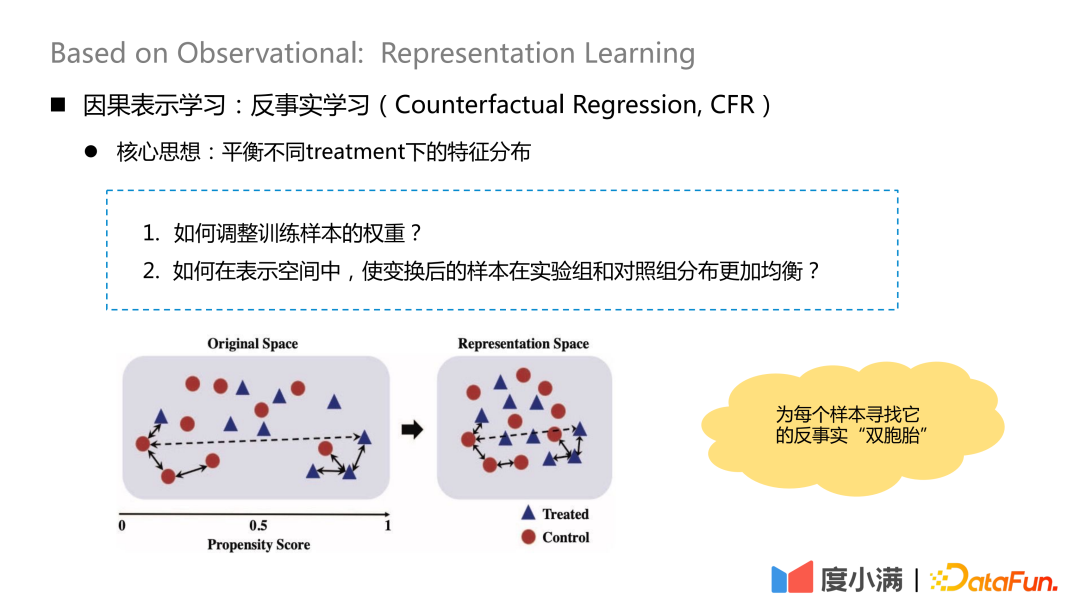
反事实学习的核心思想就是平衡不同treatment下的特征分布。
核心问题有两个:
1. 如何调整训练样本的权重?
2. 如何在表示空间中,使变换后的样本在实验组和对照组分布更加均衡?
本质思想是在变换映射后,为每个样本寻找它的反事实“双胞胎”。映射之后treatment组和control组X的分布比较相似。
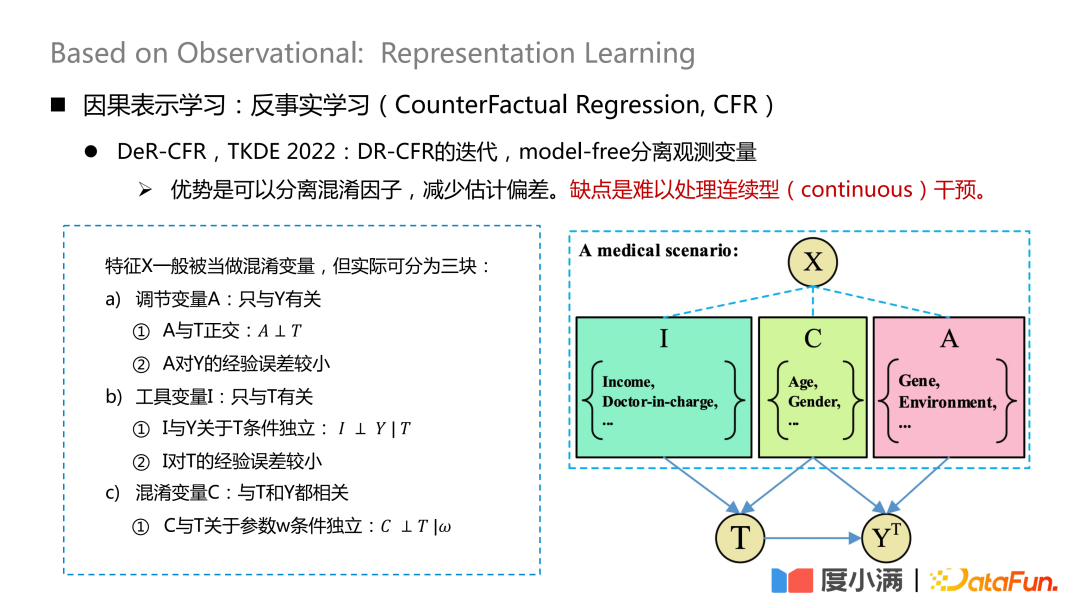
比较有代表性的工作是发表在TKDE 2022上面的一篇论文,介绍了DeR-CFR的一些工作,这部分其实是DR-CRF模型的迭代,采用model-free的方式分离观测变量。
将X变量分成三块:调节变量A,工具变量I和混淆变量C。之后再通过I,C,A来调节不同treatment下X的权重,达到在观测数据上进行因果建模的目的。
这种方法的优势是可以分离混淆因子,减少估计偏差。缺点是难以处理连续型干预。
这个网络的核心就是如何分离A/I/C三类变量。调节变量A只与Y有关,需要保证A与T正交,并且A对Y的经验误差较小;工具变量I只与T有关,需要满足I与Y关于T条件独立,并且I对T的经验误差较小;混淆变量C与T和Y都相关,w是网络的权重,给了网络权重后,需要保证C与T关于w条件独立。这里的正交性可以通过一般的距离公式实现,比如logloss或者mse欧氏距离等约束。
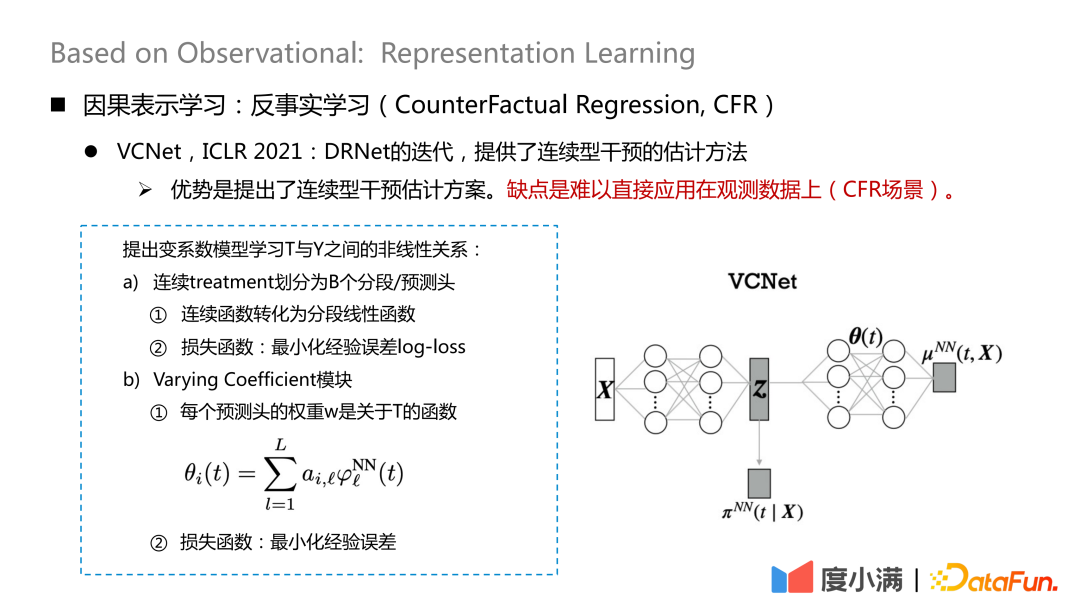
如何处理连续型干预,这块也是有一些新的论文研究,发表在ICLR2021上的VCNet,提供了连续型干预的估计方法。缺点是难以直接应用在观测数据上(CFR场景)。
将X映射到Z上,Z主要包含之前提到的X分解中的I变量和C变量,即将对treatment比较有贡献的变量从X中提取出来了。这里将连续treatment划分为B个分段/预测头,每个连续函数转化成分段的线性函数,最下化经验误差log-loss,用来学习
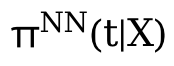
之后再用学完的Z和θ(t)去学习。 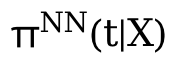
三、反事实额度模型 Mono-CFR
最后来介绍一下度小满的反事实额度模型,这里主要解决的是在观测数据上对连续型Treatment的反事实估计问题。
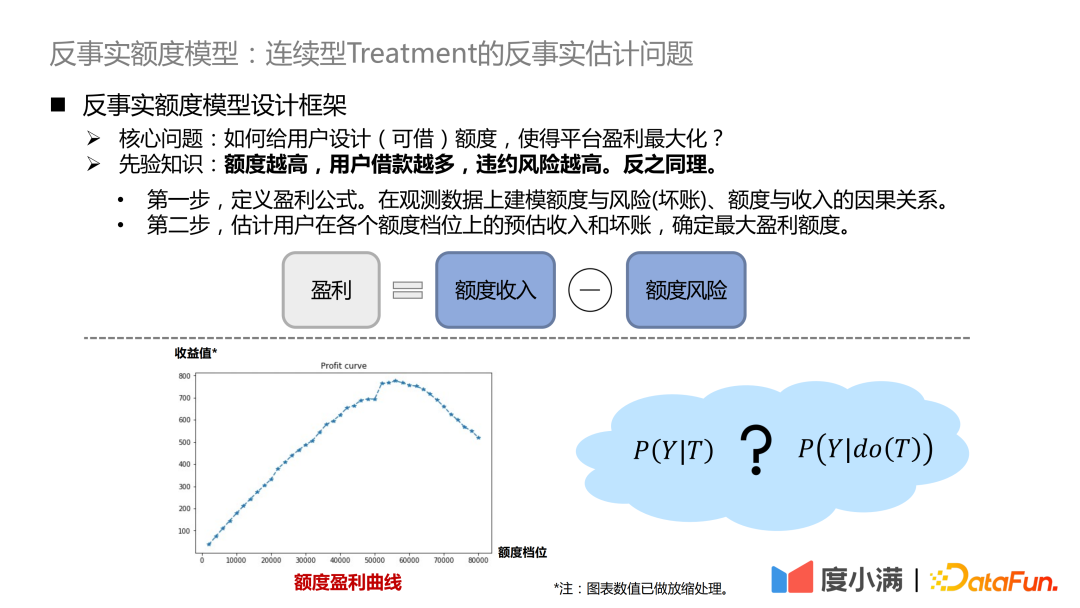
核心问题是,如何给用户设计(可借)额度,使得平台盈利最大化?这里的先验知识是,额度越高,用户借款越多,违约风险越高。反之同理。
- 第一步,定义盈利公式。盈利=额度收入-额度风险。公式看起来简单,但实际上会有很多细节的调整。这样,问题就转化为了在观测数据上建模额度与风险(坏账)、额度与收入的因果关系。
- 第二步,估计用户在各个额度档位上的预估收入和坏账,确定最大盈利额度。
我们期望对每个用户有如上图所示的一个盈利曲线,在不同的额度档位上,对收益值做反事实预估。
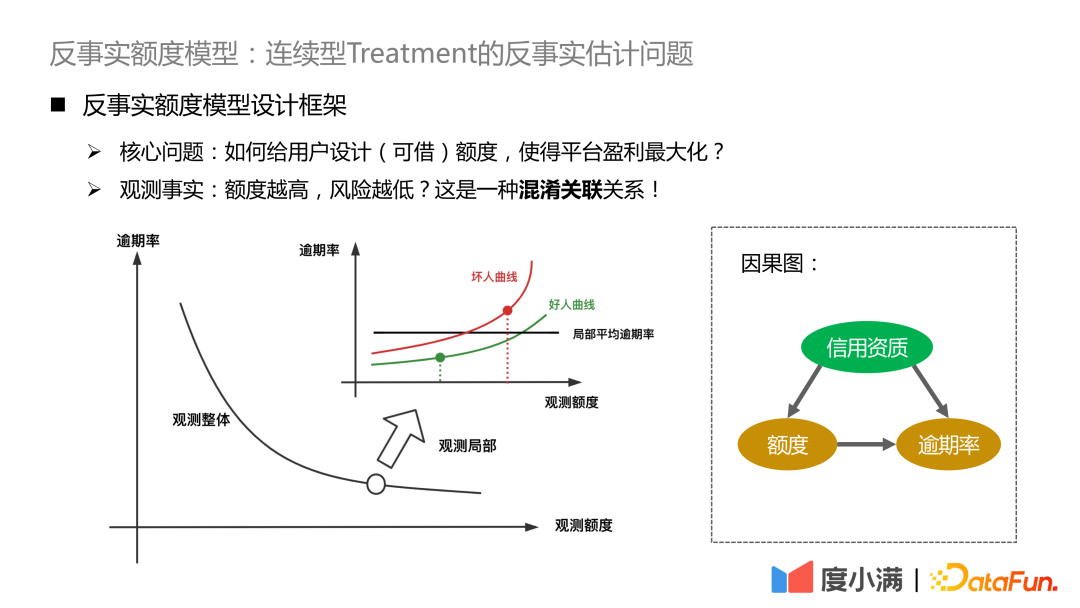
如果在观测数据上看到额度越高风险越低,本质上是由于混淆因子的存在。我们场景里的混淆因子是信用资质。信用资质比较好的人,平台会赋予更高的额度,反之则赋予较低额度。优信用资质人群的绝对风险仍旧明显低于低信用资质人群。若拉齐信用资质,会看到额度的提升将带来风险的提升,高额度突破了用户自身的偿债能力。
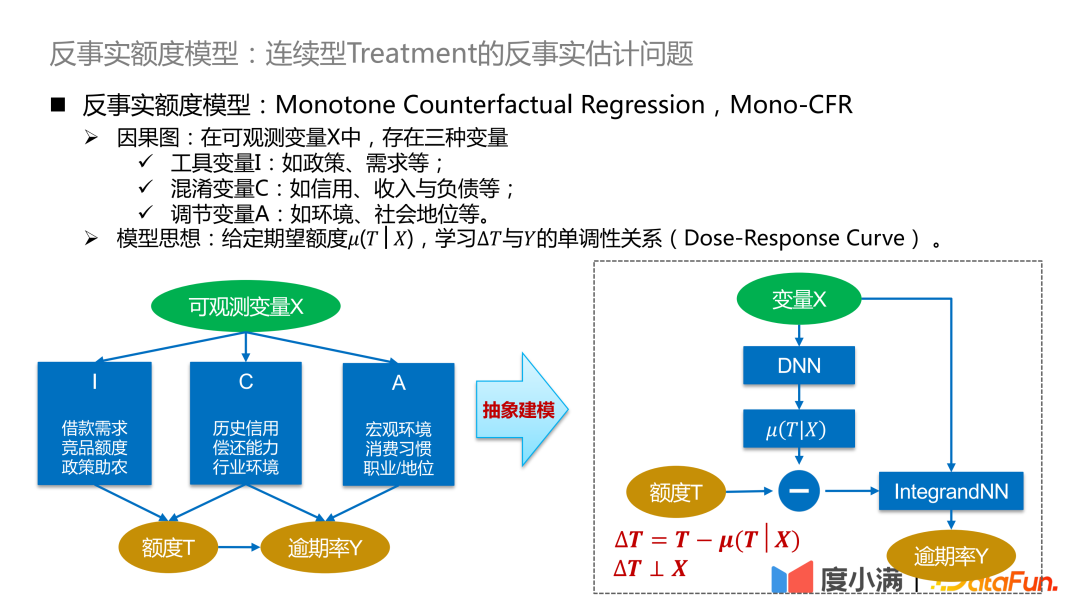
我们开始介绍反事实额度模型的框架。在可观测变量X中,存在之前提到的三种变量,其中大多数是混淆变量C,小部分是策略未考虑到的是调节变量A,还有一部分是仅仅跟干预有关系的工具变量I。
- 工具变量I:如政策、需求等,会影响历史的定额策略,但不会影响逾期概率。
- 混淆变量C:如信用、收入与负债等,同时影响对额度的调整,和这个人的逾期概率。
- 调节变量A:如环境、社会地位等,会影响逾期率。
模型思想:给定期望额度μ(T|X),学习∆T与Y的单调性关系(Dose-Response Curve)。期望额度可以理解为模型学习到的连续性倾向额度,使得混淆变量C和额度T之间的关系能够断开,转换成∆T与Y的因果关系学习,从而对∆T下Y的分布进行较好的刻画。
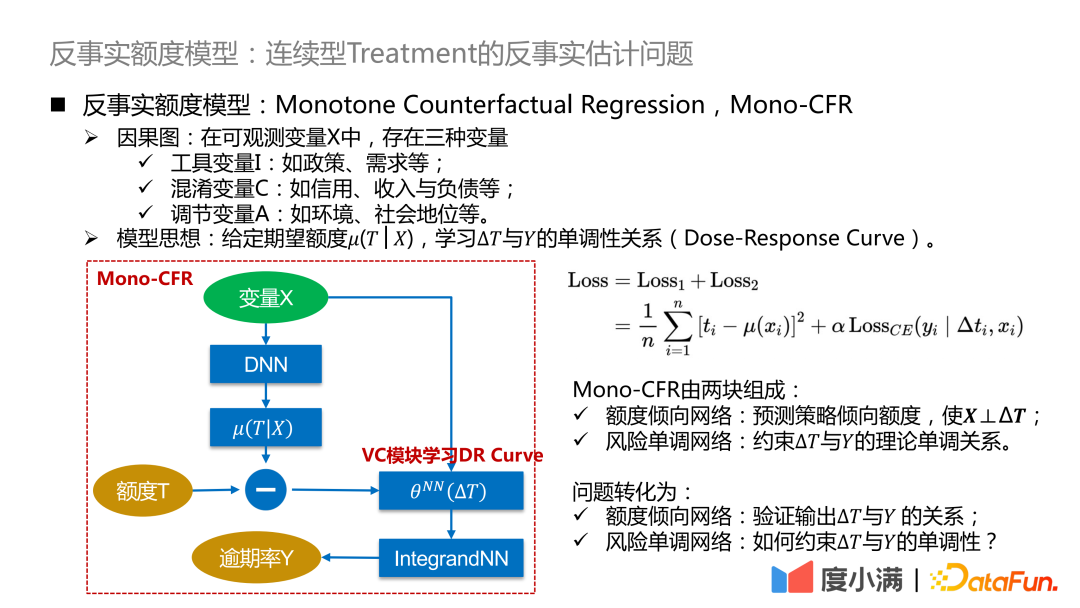
这里进一步细化上述抽象的框架:将∆T转化成变系数模型,再接入IntegrandNN网络,训练误差分成两部分:
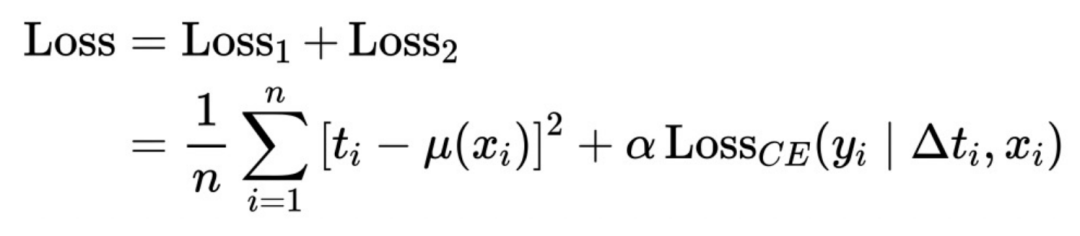
这里的α是衡量风险重要程度的超参数。
Mono-CFR由两大部分组成:
- 额度倾向网络:预测策略倾向额度,使X⊥∆T。
作用一:蒸馏出X中与T最相关的变量,最小化经验误差。
作用二:锚定历史策略上的近似样本。
- 风险单调网络:约束∆T与Y的理论单调关系。
作用一:对弱系数变量施加独立单调约束。
作用二:减少估计偏差。
问题转化为:
- 额度倾向网络:验证输出∆T与Y 的关系。
- 风险单调网络:如何约束∆T与Y的单调性?
实际额度倾向网络输入如下:
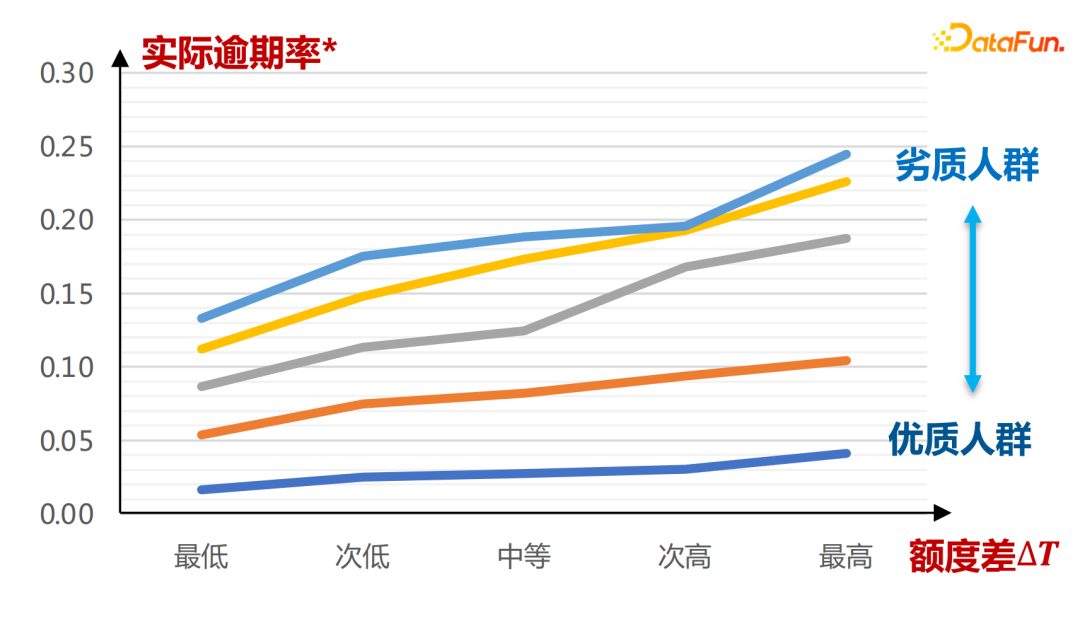
横轴是A卡评分定义出的人群,可以看出,不同倾向额度μ(T|X)下,额度差∆T与逾期率Y呈现单调递增关系,越劣质人群的额度差∆T变化曲线越陡峭,实际逾期率变化曲线也越陡峭,整个曲线斜率更大。此处的结论完全是通过历史的数据学习得出的。
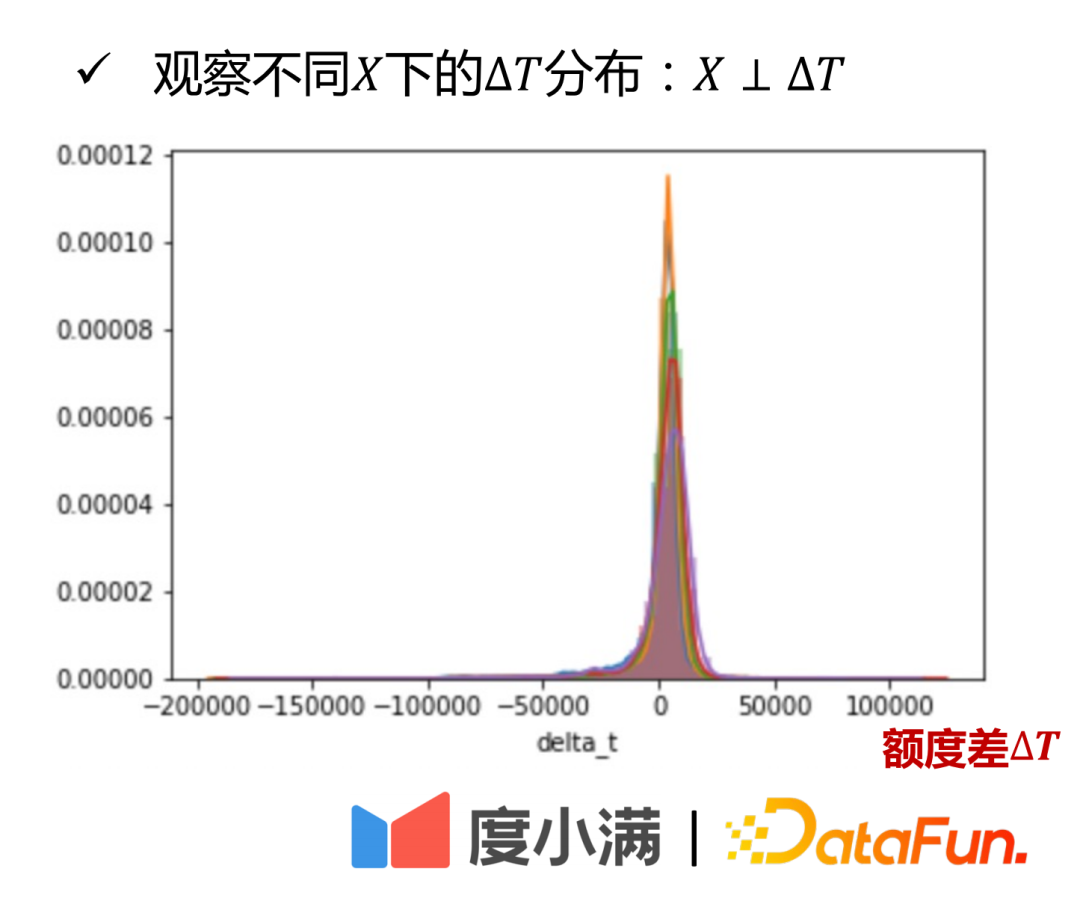
从X和∆T分布图中可以看出:不同资质人群(图中通过不同颜色区分)的额度差∆T均匀分布在相似的区间之中,这是从实际角度说明。
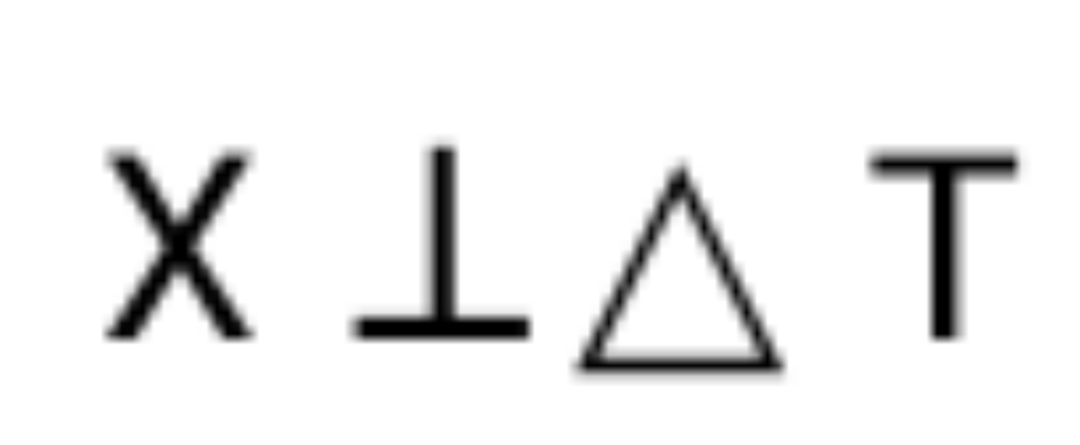
从理论角度,亦可被严格证明。
第二部分是风险单调网络的实现:

这里的ELU+1函数数学表达式为:
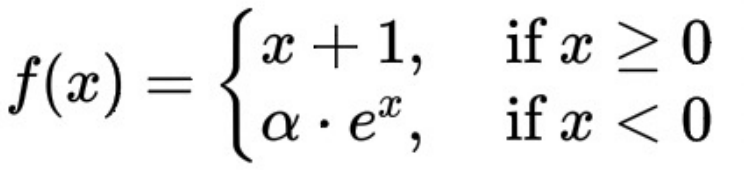
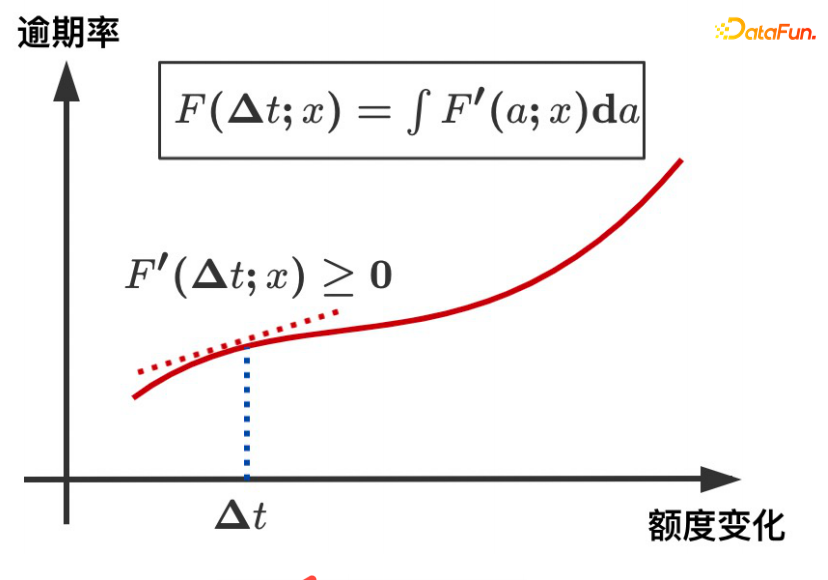
∆T和逾期率呈现单调递增的变化趋势,通过ELU+1函数的导数总是大于等于0来保证。
接下来说明风险单调网络如何对弱系数变量学的更加准确:
假设有这样一个公式:
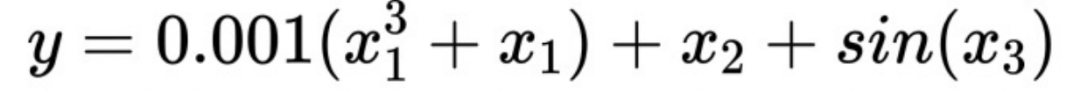
可以看出这里的x1即为弱系数变量,当对x1施加单调性约束后,对响应Y的估计更加准确。如果没有这样的单独约束,x1的重要性会被x2淹没,导致模型偏差增大。
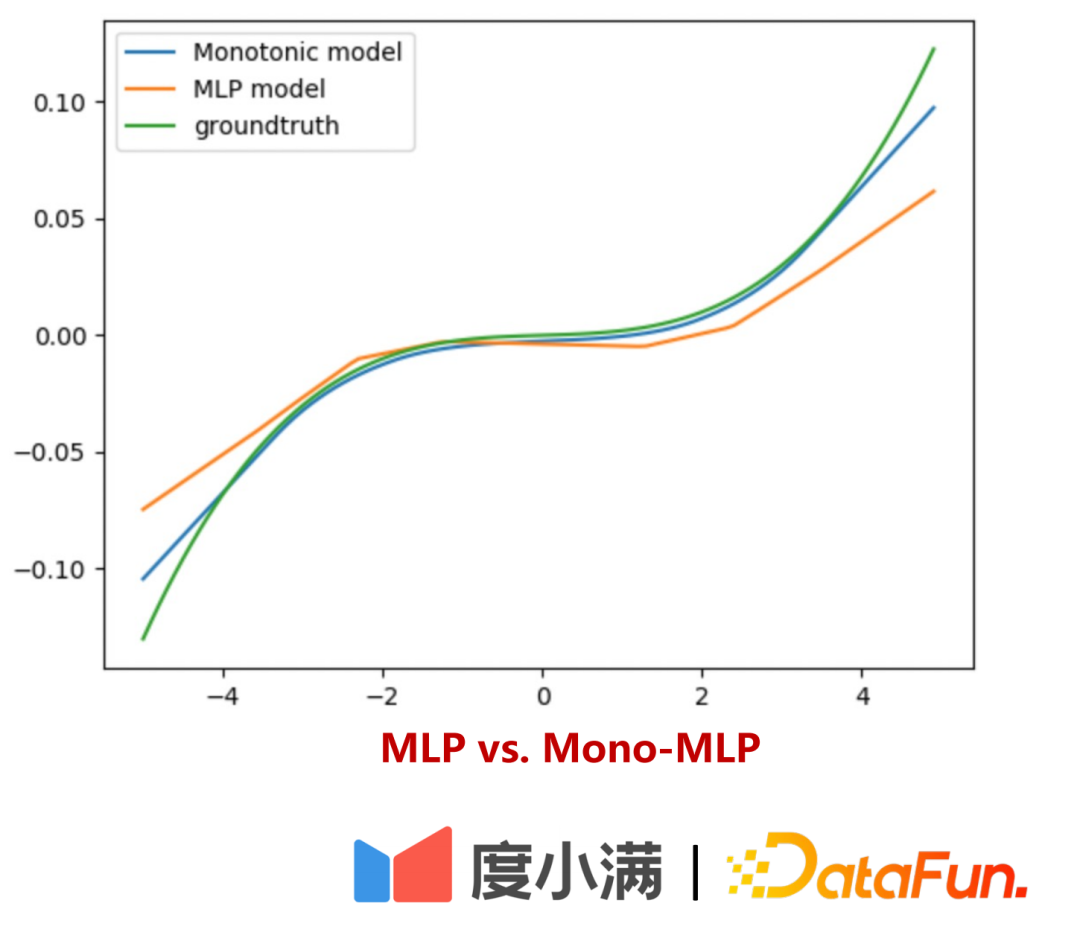
如何离线评估额度的风险的估计曲线?
分成两部分:
- 第一部分:可解释验证
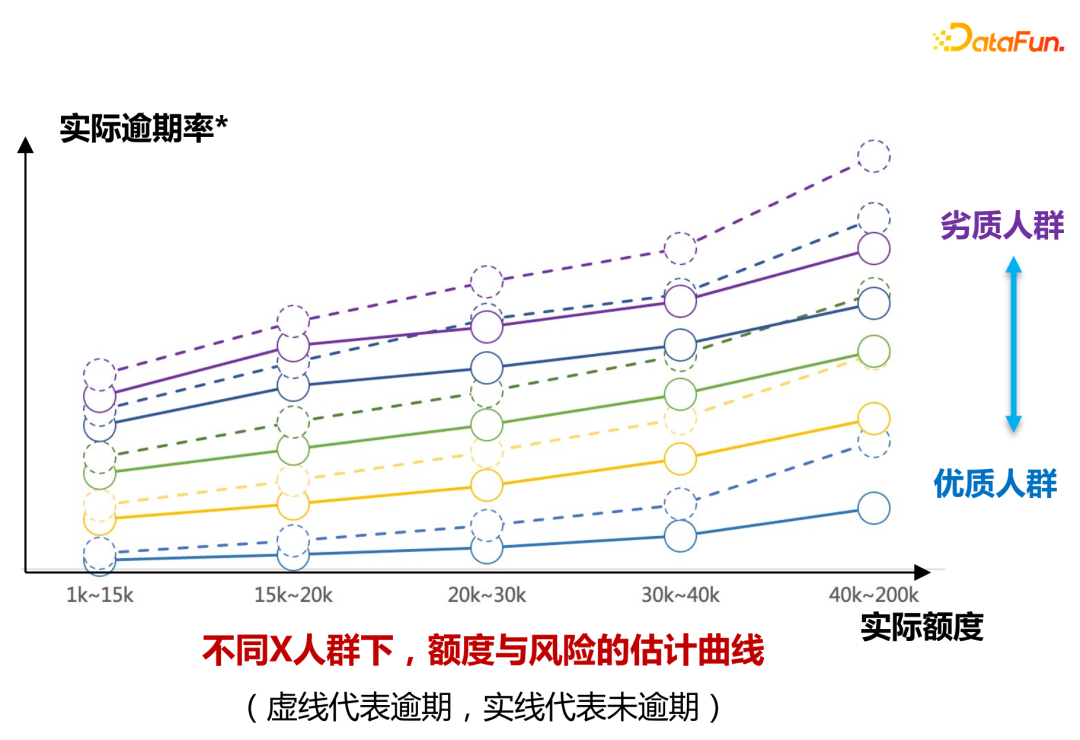
不同资质人群下,去绘制如上图所示的额度风险变化曲线,模型可以学出不同资质人群(图中不同颜色标识)不同档位实际额度和逾期率的区分度。
- 第二部分:利用小流量实验验证,不同提额幅度下的风险偏差,可以通过uplift分箱得出。
线上实验结论:
在额度上涨30%条件下,用户逾期金额下降20%以上, 借款提升30%,盈利性提升 30%以上。
未来模型预期:
以model-free形式将工具变量与调节变量更清晰地分开,使模型在劣质人群上的风险迁移表现更佳。
在实际业务场景中,度小满的模型演进迭代流程如下:
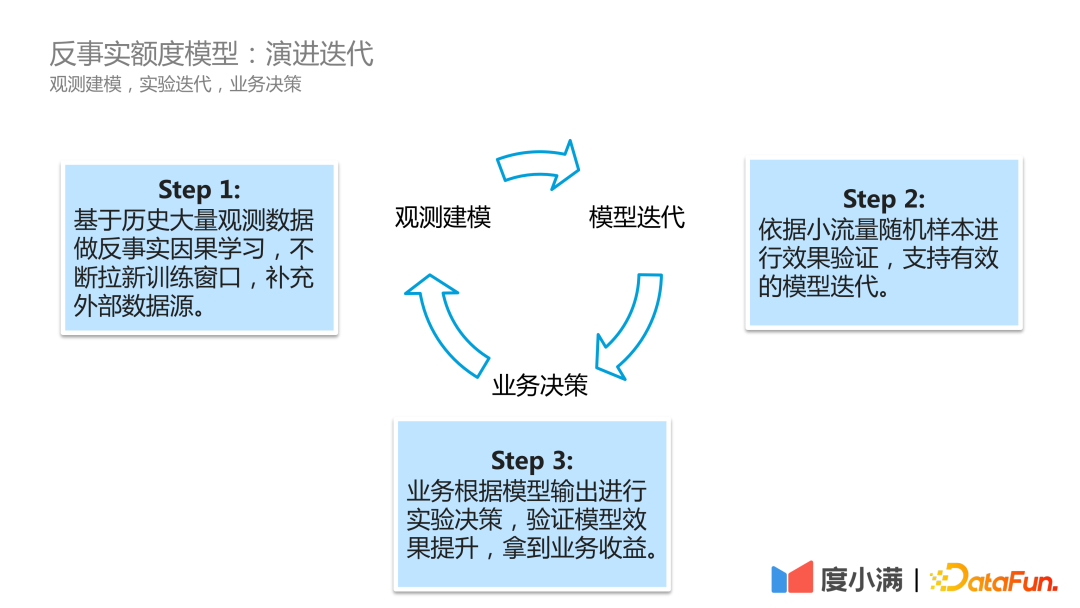
第一步,观测建模,不断滚动历史观测数据,去做反事实因果学习,不断拉新训练窗口,补充外部数据源。
第二步,模型迭代,依据小流量随机样本进行效果验证,支持有效的模型迭代。
第三步,业务决策,业务根据模型输出进行实验决策,验证模型效果提升,拿到业务收益。










































