JS数值存储运算原理-51CTO.COM

前言

相信大家都看过这些曾经在社区比较火的文章：

0.1 + 0.2 与0.3为什么不相等?
为什么 3.0000000000000002 === 3表达式为true ?
等...

造成这些问题的背后原因都是由于javaScript采用了 IEEE754 标准，全称 IEEE 二进制浮点数算术标准。所以说这个问题其实不止是会在javaScript中出现，而是「其他遵循 [IEEE 754]标准的语言也会出现这个问题」

并且自己在最近的工作中也遇到了这个问题，由于javaScript精度丢失而造成诡异问题！

javaScript车祸现场

上面三个例子在我们在控制台里面验证一遍，是不是瞬间觉得奇怪的知识又增加了？

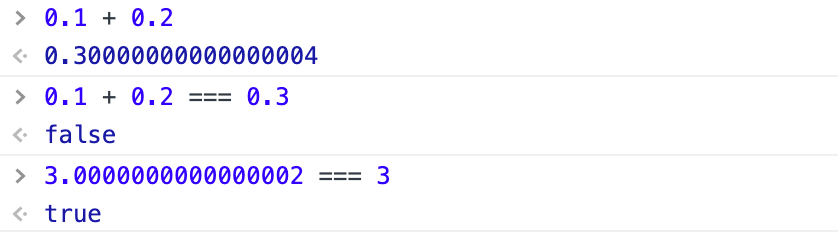
javaScript这令人窒息的操作是不是让很多后端人员口吐芬芳了，甚至是很多前端人员都觉得明明都是送分题，却成了JS的送命题，工作中许多不经意间写出的bug，往往是由于JS的不按常理出牌。

说了这么多，我们也改变不了这一现状，那就尝试去理解它吧～

计算机运算

学过计算机相关同学都知道，我们的计算机底层元算采用的是二进制，而不是我们平常用的十进制！

二进制

「为什么计算机要采用二进制，而不是十进制？」

以下是在知乎上看到的回答，我觉得这个理解是比较到位的。

计算机本身的理论模型，和采用哪个数学上的进制完全无关，十进制也好，五进制也好，二进制也好，进制在数学上都是等价的，并没有哪个进制拥有其他进制无法实现的计算。
但计算机的实现是个工程问题，需要和真实的物理环境打交道，我们现在是用电路去实现我们的计算机模型，那就需要和物理电路打交道，需要考虑到信号的衰减延迟，电路器件的各种电气特性，什么电磁波干扰电流扰动，也就是会有失真的情况出现，而要最大程度避免衰减，失真对计算机这个完美世界造成破坏，同时要考虑电路的设计，制作成本，就需要最简单化的物理实现方案。
电子计算机确实是可以做成十进制的，就像题主说的像灯泡亮度分成十种亮度那样，但与此同时会出现很多的工程问题，比如对电子器件的精度和稳定性要求很高，电路设计的复杂性提升等等，到头来还不如就用二进制，在成本和质量上最划算。
事实上，不但十进制不行，十六进制、八进制、四进制也都比不上二进制。理论上已经证明效率最高的进制是e，离e最近的其实是三进制。但三进制不方便表示，不过也有人研究，前苏联就做过三进制计算机，国内也有，但并没有走出实验室。效率是一方面，实现成本又是一方面，最终大家还是觉得二进制实现起来最方便。

原码、反码、补码

「为运算方便，机器数有 3 种表示法，即原码、反码和补码」。

原码

原码是一种计算机中对数字的二进制定点表示法。「原码表示法在数值前面增加了一位符号位」。

反码

正数的反码和原码一样，

负数的反码就是在原码的基础上符号位保持不变，其他位取反。

补码

正数和 0 的补码就是该数字本身。

「负数的补码则是将其对应正数按位取反再加 1」

二进制转换

「正整数的转换方法」：除二取余，然后倒序排列，高位补零。

例如21的转换

商  余
21/2  10  1
10/2  5   0
5/2   2   1
2/2   1   0
1/2   0   1

21的二进制为10101，然后高位补0为00010101

「负整数的转换方法」：将对应的正整数转换成二进制后，对二进制取反，然后对结果再加一。

例如-21
先把21转换成二进制 00010101
逐位取反：11101010
再加1：11101011（补码）

「小数的转换方法」：对小数点以后的数乘以2，取整数部分，再取小数部分乘2，以此类推……直到小数部分为0或位数足够。取整部分按先后顺序排列即可。

例如123.4:
0.4*2=0.8 ——————-> 取0
0.8*2=1.6 ——————-> 取1
0.6*2=1.2 ——————-> 取1
0.2*2=0.4 ——————-> 取0
0.4*2=0.8 ——————-> 取0
………… 后面就是循环了
按顺序写出：0.4 = 0.01100110……（0110循环）
整数部分123的二进制是 1111011
则123.4的二进制表示为：1111011.011001100110……

发现了什么？十进制小数转二进制后大概率出现无限位数！但我们的javaScript采用了「IEEE754」标准，全称「IEEE 二进制浮点数算术标准」。

由于IEEE 754尾数位数限制，会将后面多余的位截掉。

javaScript 与 IEEE 754

“JavaScript 采用 IEEE 754 标准，数值存储为64位双精度格式，数值精度最多可以达到 53 个二进制位（1 个隐藏位与 52 个有效位）

在这个标准下，我们会用1位存储 S(sign)，0 表示正数，1 表示负数。用11位存储 E(exponent) + bias，对于11位来说，bias 的值是 2^(11-1) - 1，也就是 1023。用52 位存储 Fraction。

由于javaScript采用的是IEE754标准，所以在进制之间的转换过程中可能会导致精度丢失，这是造成javaScript运算翻车的罪魁祸首！

破案

0.1+0.2 与 0.3为什么不相等？

0.1.toString(2)
// '0.0001100110011001100110011001100110011001100110011001101'   // 57
// 按 IEEE754 格式  57 - 4 = 52可以精确存储
0.2.toString(2)
// '0.001100110011001100110011001100110011001100110011001101' // 56
// 按 IEEE754 格式  56 - 3 = 53  会丢弃最后一位数
0.3.toString(2)
// '0.010011001100110011001100110011001100110011001100110011'  // 56
// 按 IEEE754 格式  56 - 2 = 54  会丢弃最后两位数

/*总结：
存储0.1没有误差， 存储 0.2丢弃最后一位 1  存储0.3丢弃最后2位 11，
显然存储0.3丢弃的数值>存储0.2丢弃的数值
经分析 0.1 + 0.2   应该大于 0.3
*/
0.1 + 0.2 > 0.3  // true

为什么 3.0000000000000002 === 3表达式为true ?

手动将 3.0000_0000_0000_0002转换成二进制浮点数

整数部分为 11₂

小数部分0.0000_0000_0000_0002

0.0000_0000_0000_0002.toString(2)

'0.0000000000000000000000000000000000000000000000000000111001101001010110010100101111101100010001001101111'

注意小数点后面正好有52个0

0.0000_0000_0000_0002.toString(2).length  // 105 105

将 3.0000000000000002 用 IEEE754 格式表示

符号S: 正数，0
指数位E：11 = 1.1 * 2^1 (二进制)，E = 1023 + 1 = 1024 = 10000000000(二进制)
尾数位M：0.1.....0

所以该浮点数格式为: 0 1000_0000_000 1...000(一共52个0) 这个数正好是3。

如何解决精度问题？

目前有许多第三方库可以解决javaScript精度丢失的问题

math.js

math.js是JavaScript和Node.js的一个广泛的数学库。支持数字，大数，复数，分数，单位和矩阵等数据类型的运算。

官网：mathjs.org/ GitHub：github.com/josdejong/m…

0.1+0.2 ===0.3实现代码：

var math = require('mathjs')
console.log(math.add(0.1,0.2))//0.30000000000000004
console.log(math.format((math.add(math.bignumber(0.1),math.bignumber(0.2)))))//'0.3'

decimal.js

为 JavaScript 提供十进制类型的任意精度数值。

官网：mikemcl.github.io/decimal.js/

GitHub：github.com/MikeMcl/dec…

var Decimal = require('decimal.js')
x = new  Decimal(0.1)
y = 0.2
console.log(x.plus(y).toString())//'0.3'

bignumber.js

用于任意精度算术的JavaScript库。

官网：mikemcl.github.io/bignumber.j…

Github：github.com/MikeMcl/big…

var BigNumber = require("bignumber.js")
x = new BigNumber(0.1)
y = 0.2
console.log(x.plus(y).toString()) //'0.3'