译者 | 李睿
审校 | 重楼
人工神经网络是深度学习的一种形式，也是现代人工智能的支柱之一。用户真正掌握其工作原理的最佳方法是自己构建一个人工神经网络。本文将介绍如何用Java构建和训练神经网络。
感兴趣的用户可以查阅软件架构师Matthew Tyson以前撰写的名为《机器学习的风格：神经网络简介》文章，以了解人工神经网络如何运行的概述。本文中的示例将不是一个生产等级的系统，与其相反，它在一个易于理解的演示例子中展示了所有的主要组件。
一个基本的神经网络
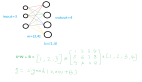
神经网络是一种称为神经元（Neuron）的节点图。神经元是计算的基本单位。它接收输入并使用每个输入的权重、每个节点的偏差和最终函数处理器(其名称为激活函数)算法处理它们。例如图1所示的双输入神经元。
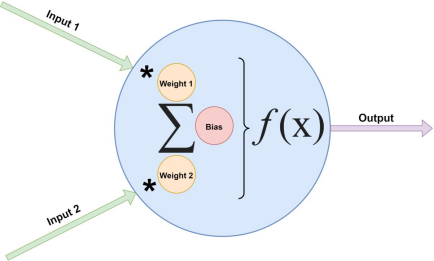
图1 神经网络中的双输入神经元
这个模型具有广泛的可变性，将在下面演示的例子中使用这个精确的配置。
第一步是建立一个神经元类模型，该类将保持这些值。可以在清单1中看到神经元类。需要注意的是，这是该类的第一个版本。它将随着添加的功能而改变。
清单1.简单的神经元类
class Neuron {
Random random = new Random();
private Double bias = random.nextDouble(-1, 1);
public Double weight1 = random.nextDouble(-1, 1);
private Double weight2 = random.nextDouble(-1, 1);
public double compute(double input1, double input2){
double preActivation = (this.weight1 * input1) + (this.weight2 * input2) + this.bias;
double output = Util.sigmoid(preActivation);
return output;
}
}可以看到神经元（Neuron）类非常简单，有三个成员：bias、weight1和weight2。每个成员被初始化为－1到1之间的随机双精度。
当计算神经元的输出时，遵循图1所示的算法：将每个输入乘以其权重，再加上偏差：input1 * weight1 + input2 * weight2 + biass。这提供了通过激活函数运行的未处理计算(即预激活)。在本例中，使用Sigmoid激活函数，它将值压缩到－1到1的范围内。清单2显示了Util.sigmoid()静态方法。
清单2.Sigmoid激活函数
public class Util {
public static double sigmoid(double in){
return 1 / (1 + Math.exp(-in));
}
}现在已经了解了神经元是如何工作的，可以把一些神经元放到一个网络中。然后将使用带有神经元列表的Network类，如清单3所示。
清单3.神经网络类
class Network {
List<Neuron> neurons = Arrays.asList(
new Neuron(), new Neuron(), new Neuron(), /* input nodes */
new Neuron(), new Neuron(), /* hidden nodes */
new Neuron()); /* output node */
}
}虽然神经元的列表是一维的，但将在使用过程中将它们连接起来，使它们形成一个网络。前三个神经元是输入，第二个和第三个是隐藏的，最后一个是输出节点。
进行预测
现在，使用这个网络来做一个预测。将使用两个输入整数的简单数据集和0到1的答案格式。这个例子使用体重-身高组合来猜测某人的性别，这是基于这样的假设，即体重和身高越高，则表明某人是男性。可以对任何两个因素使用相同的公式，即单输出概率。可以将输入视为一个向量，因此神经元的整体功能将向量转换为标量值。
网络的预测阶段如清单4所示。
清单4.网络预测
public Double predict(Integer input1, Integer input2){
return neurons.get(5).compute(
neurons.get(4).compute(
neurons.get(2).compute(input1, input2),
neurons.get(1).compute(input1, input2)
),
neurons.get(3).compute(
neurons.get(1).compute(input1, input2),
neurons.get(0).compute(input1, input2)
)
);
}清单4显示了将两个输入馈入到前三个神经元，然后将前三个神经元的输出馈入到神经元4和5，神经元4和5又馈入到输出神经元。这个过程被称为前馈。
现在，可以要求网络进行预测，如清单5所示。
清单5.获取预测
Network network = new Network();
Double prediction = network.predict(Arrays.asList(115, 66));
System.out.println(“prediction: “ + prediction);在这里肯定会得到一些结果，但这是随机权重和偏差的结果。为了进行真正的预测，首先需要训练网络。
训练网络
训练神经网络遵循一个称为反向传播的过程。反向传播基本上是通过网络向后推动更改，使输出向期望的目标移动。
可以使用函数微分进行反向传播，但在这个例子中，需要做一些不同的事情，将赋予每个神经元“变异”的能力。在每一轮训练(称为epoch)中，选择一个不同的神经元对其属性之一(weight1,weight2或bias)进行小的随机调整，然后检查结果是否有所改善。如果结果有所改善，将使用remember()方法保留该更改。如果结果恶化，将使用forget()方法放弃更改。
添加类成员(旧版本的权重和偏差)来跟踪变化。可以在清单6中看到mutate()、remember()和forget()方法。
清单6.Mutate()，remember()，forget()
public class Neuron() {
private Double oldBias = random.nextDouble(-1, 1), bias = random.nextDouble(-1, 1);
public Double oldWeight1 = random.nextDouble(-1, 1), weight1 = random.nextDouble(-1, 1);
private Double oldWeight2 = random.nextDouble(-1, 1), weight2 = random.nextDouble(-1, 1);
public void mutate(){
int propertyToChange = random.nextInt(0, 3);
Double changeFactor = random.nextDouble(-1, 1);
if (propertyToChange == 0){
this.bias += changeFactor;
} else if (propertyToChange == 1){
this.weight1 += changeFactor;
} else {
this.weight2 += changeFactor;
};
}
public void forget(){
bias = oldBias;
weight1 = oldWeight1;
weight2 = oldWeight2;
}
public void remember(){
oldBias = bias;
oldWeight1 = weight1;
oldWeight2 = weight2;
}
}非常简单：mutate()方法随机选择一个属性，随机选择-1到1之间的值，然后更改该属性。forget()方法将更改滚回旧值。remember()方法将新值复制到缓冲区。
现在，为了利用神经元的新功能，我们向Network添加了一个train()方法，如清单7所示。
清单7.Network.train()方法
public void train(List<List<Integer>> data, List<Double> answers){
Double bestEpochLoss = null;
for (int epoch = 0; epoch < 1000; epoch++){
// adapt neuron
Neuron epochNeuron = neurons.get(epoch % 6);
epochNeuron.mutate(this.learnFactor);
List<Double> predictions = new ArrayList<Double>();
for (int i = 0; i < data.size(); i++){
predictions.add(i, this.predict(data.get(i).get(0), data.get(i).get(1)));
}
Double thisEpochLoss = Util.meanSquareLoss(answers, predictions);
if (bestEpochLoss == null){
bestEpochLoss = thisEpochLoss;
epochNeuron.remember();
} else {
if (thisEpochLoss < bestEpochLoss){
bestEpochLoss = thisEpochLoss;
epochNeuron.remember();
} else {
epochNeuron.forget();
}
}
}train（）方法对数据重复1000次，并在参数中保留回答列表。这些是同样大小的训练集；数据保存输入值，答案保存已知的良好答案。然后，该方法遍历这些答案，并得到一个值，表明网络猜测的结果与已知的正确答案相比的正确率。然后，它会让一个随机的神经元发生突变，如果新的测试表明这是一个更好的预测，它就会保持这种变化。
检查结果
可以使用均方误差(MSE)公式来检查结果，这是一种在神经网络中测试一组结果的常用方法。可以在清单8中看到MSE函数。
清单8.均方误差函数
public static Double meanSquareLoss(List<Double> correctAnswers, List<Double> predictedAnswers){
double sumSquare = 0;
for (int i = 0; i < correctAnswers.size(); i++){
double error = correctAnswers.get(i) - predictedAnswers.get(i);
sumSquare += (error * error);
}
return sumSquare / (correctAnswers.size());
}微调系统
现在剩下的就是把一些训练数据输入网络，并用更多的预测来尝试。清单9显示了如何提供训练数据。
清单9.训练数据
List<List<Integer>> data = new ArrayList<List<Integer>>();
data.add(Arrays.asList(115, 66));
data.add(Arrays.asList(175, 78));
data.add(Arrays.asList(205, 72));
data.add(Arrays.asList(120, 67));
List<Double> answers = Arrays.asList(1.0,0.0,0.0,1.0);
Network network = new Network();
network.train(data, answers);在清单9中，训练数据是一个二维整数集列表(可以把它们看作体重和身高)，然后是一个答案列表(1.0表示女性，0.0表示男性)。
如果在训练算法中添加一些日志记录，运行它将得到类似清单10的输出。
清单10.记录训练器
// Logging:
if (epoch % 10 == 0) System.out.println(String.format("Epoch: %s | bestEpochLoss: %.15f | thisEpochLoss: %.15f", epoch, bestEpochLoss, thisEpochLoss));
// output:
Epoch: 910 | bestEpochLoss: 0.034404863820424 | thisEpochLoss: 0.034437939546120
Epoch: 920 | bestEpochLoss: 0.033875954196897 | thisEpochLoss: 0.431451026477016
Epoch: 930 | bestEpochLoss: 0.032509260025490 | thisEpochLoss: 0.032509260025490
Epoch: 940 | bestEpochLoss: 0.003092720117159 | thisEpochLoss: 0.003098025397281
Epoch: 950 | bestEpochLoss: 0.002990128276146 | thisEpochLoss: 0.431062364628853
Epoch: 960 | bestEpochLoss: 0.001651762688346 | thisEpochLoss: 0.001651762688346
Epoch: 970 | bestEpochLoss: 0.001637709485751 | thisEpochLoss: 0.001636810460399
Epoch: 980 | bestEpochLoss: 0.001083365453009 | thisEpochLoss: 0.391527869500699
Epoch: 990 | bestEpochLoss: 0.001078338540452 | thisEpochLoss: 0.001078338540452清单10显示了损失（误差偏离正右侧）缓慢下降；也就是说，它越来越接近做出准确的预测。剩下的就是看看模型对真实数据的预测效果如何，如清单11所示。
清单11.预测
System.out.println("");
System.out.println(String.format(" male, 167, 73: %.10f", network.predict(167, 73)));
System.out.println(String.format("female, 105, 67: %.10", network.predict(105, 67)));
System.out.println(String.format("female, 120, 72: %.10f | network1000: %.10f", network.predict(120, 72)));
System.out.println(String.format(" male, 143, 67: %.10f | network1000: %.10f", network.predict(143, 67)));
System.out.println(String.format(" male', 130, 66: %.10f | network: %.10f", network.predict(130, 66)));在清单11中，将训练好的网络输入一些数据，输出预测结果。结果如清单12所示。
清单12.训练有素的预测
male, 167, 73: 0.0279697143
female, 105, 67: 0.9075809407
female, 120, 72: 0.9075808235
male, 143, 67: 0.0305401413
male, 130, 66: network: 0.9009811922在清单12中，看到网络对大多数值对(又名向量)都做得很好。它给女性数据集的估计值约为0.907，非常接近1。两名男性显示0.027和0.030接近0。离群的男性数据集(130,67)被认为可能是女性，但可信度较低，为0.900。
结论
有多种方法可以调整这一系统上的参数。首先，训练运行中的epoch数是一个主要因素。epoch越多，其模型就越适合数据。运行更多的epoch可以提高符合训练集的实时数据的准确性，但也会导致过度训练。也就是说，这是一个在边缘情况下自信地预测错误结果的模型。
文章标题：How to build a neural network in Java，作者：Matthew Tyson
