「BFS的核心思想是把一些问题抽象成图,从一个点开始,向四周开始扩散。一般来说,写BFS算法都是用队列这种数据结构,每次将一个节点周围的所有节点加入队列。」
「BFS相对于DFS的最主要的区别是:BFS找到的路径一定是最短的,但代价就是空间复杂度比DFS大很多。」
「BFS出现的常见场景:问题的本质就是让你在一幅图中找到从起点start到终点target的最近距离」
二叉树的最小深度
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
示例 1:
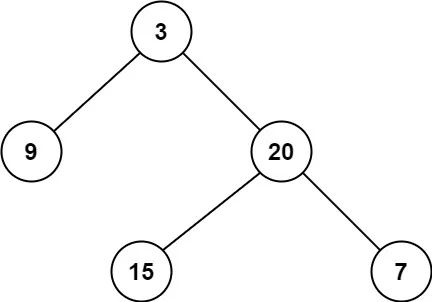
输入:root = [3,9,20,null,null,15,7] 输出:2
// 找最短路径,用BFS
// 1. 首先明确起点start和终点target是什么?
// 起点就是root根节点,终点就是最靠近根节点的那个叶子节点
// 2、 怎么判断达到了终点
// 叶子节点就是两个子节点都是null的节点
function minDepth(root) {
const bfs = (root) => {
if (!root) {
return 0;
}
// root本身就是一层,depth初始化为1
let depth = 1;
const queue = [root];
while (queue.length > 0) {
const size = queue.length;
// 遍历当前存在队列中的数据
for (let i = 0; i < size; i++) {
const cur = queue.shift();
// 将左右子节点存入队列
if (cur.left) {
queue.push(cur.left);
}
if (cur.right) {
queue.push(cur.right);
}
if (cur.left === null && cur.right === null) {
return depth;
}
}
// 遍历完一层之后增加步数
depth++;
}
return depth;
}
return bfs(root);
}填充每个节点的下一个右侧节点指针
给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
struct Node { int val; Node *left; Node *right; Node *next; } 填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
示例 1:
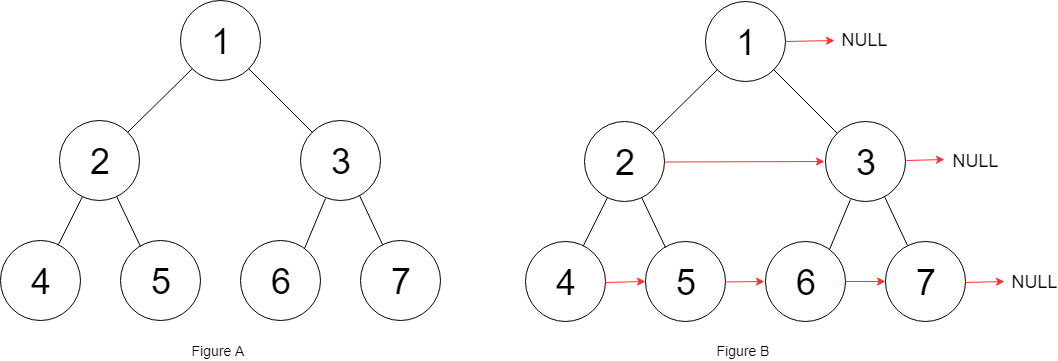
输入:root = [1,2,3,4,5,6,7] 输出:[1,#,2,3,#,4,5,6,7,#] 解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化的输出按层序遍历排列,同一层节点由 next 指针连接,'#' 标志着每一层的结束
// 典型的通过BFS解决
function connect(root) {
if (root === null) {
return root;
}
const list = [root];
while (list.length > 0) {
const size = list.length;
for (let i = 0; i < size; i++) {
const preNode = list.shift();
// 进行连接
if (i === size - 1) {
preNode.next = null;
} else {
preNode.next = list[0];
}
// 获取下一个元素,将内容填充到栈中
preNode.left && list.push(preNode.left);
preNode.right && list.push(preNode.right);
}
}
return root;
}
const root = {
val: 1,
left: {
val: 2,
left: null,
right: null
},
right: {
val: 3,
left: null,
right: null
}
};
console.log(connect(root));









































