今天是十五周算法训练营的第五周,主要讲二叉搜索树专题,包含:验证二叉搜索树、不同的二叉搜索树、二叉树的最近公共祖先、二叉搜索树的最近公共祖先。(欢迎加入十五周算法训练营,与小伙伴一起卷算法)
BST的特性:
对于BST的每一个节点node,左子树节点的值都比node的值要小,右子树节点的值都比node的值大;
对于BST的每一个节点node,它的左侧子树和右侧子树都是BST。
BST有一个重要的性质:BST的中序遍历结果是有序的(升序),也就是在中序位置可以将每个节点的值升序打印出来
void traverse(TreeNode root) {
if (root == null) return;
traverse(root.left);
// 中序遍历代码位置
print(root.val);
traverse(root.right);
}验证二叉搜索树
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
节点的左子树只包含 小于 当前节点的数。 节点的右子树只包含 大于 当前节点的数。 所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
输入:root = [2,1,3] 输出:true
根据二叉搜索树特性,通过中序遍历获取。
// 解题思路:
// 1. 是否可以通过遍历一遍二叉树得到答案?
// 通过中序遍历可以得到,因为BST的中序遍历是一个升序结果
function isValidBST1(root) {
let inorder = -Infinity;
let result = true;
let traverse = root => {
if (root === null) {
return;
}
// 前序位置
traverse(root.left);
// 中序位置
// 中序位置获取当前值,并比较其和前一个值的大小,如果小于等于前一个值,则证明不是BST树,则将结果变为false
if (root.val <= inorder) {
result = false;
} else {
inorder = root.val;
}
traverse(root.right);
// 后续位置
};
traverse(root);
return result;
}
// 将中序遍历变为循环的方式
function isValidBST2(root) {
if (root === null) {
return true;
}
let head = root;
const stack = [];
let inorder = -Infinity;
// 中序遍历的循环结构是需要创建一个栈,然后先将左节点全压入栈中
while (stack.length > 0 || head !== null) {
// 当head不为空时,压入栈中
if (head !== null) {
stack.push(head);
head = head.left;
} else {
// 弹出栈顶元素
head = stack.pop();
if (inorder >= head.val) {
return false;
}
inorder = head.val;
head = head.right;
}
}
return true;
}
// 2. 是否可以定义一个递归函数,通过子问题(子树)的答案推导出原问题的答案?
// 答案是可以的,因为搜索二叉树的性质是:
// (1)对于BST的每一个节点node,左子树节点值都比node的值要小,右子树节点的值逗比node的值大;
// (2)对于BST的每一个节点node,它的左侧子树和右侧子树都是BST
// 则我们解决该问题可定义一个递归函数来进行解决
// 注意:该问题需要借助外部变量,因为根节点的值必须大于左子树所有值、小于右子树所有值,所以需要引入最大最小值
function isValidBST3(root) {
// 构造一个辅助函数,判断根节点是否在(min,max)范围内
const helper = (root, min, max) => {
if (root === null) {
return true;
}
if (root.val <= min) {
return false;
}
if (root.val >= max) {
return false;
}
return helper(root.left, min, root.val) && helper(root.right, root.val, max);
};
// 初始状态min为-Infinity,max为Infinity
return helper(root, -Infinity, Infinity);
}不同的二叉搜索树
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 「二叉搜索树」 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:」
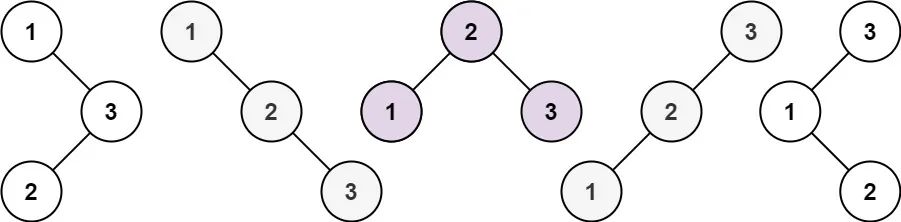
输入:n = 3
输出:5
利用的也是左子树值 < 根节点 < 右子树值
// 对于BST的每一个节点node,左子树节点的值都比node的值要小,右子树节点的值都比node的值大
// 在该问题中,1~n都有可能成为根节点,然后左边的是左子树上的点,右边的是右子树上的点,然后对应根节点的搜索树数量就是左子树的组合数 * 右子树的组合数;
// 该问题明显就转换为一个递归问题
function numTree(n) {
// 为了解决子问题的重复问题,需要引入备忘录
const memo = [];
for (let i = 0; i < n + 1; i++) {
memo.push([]);
for (let j = 0; j < n + 1; j++) {
memo[i].push(0);
}
}
const count = (low, high) => {
// 递归终止条件
if (low > high) {
return 1;
}
// 判断备忘录中是否存在该值,存在的话直接使用
if (memo[low][high] > 0) {
return memo[low][high];
}
let result = 0;
for (let i = low; i <= high; i++) {
const left = count(low, i - 1);
const right = count(i + 1, high);
result += left * right;
}
// 将结果存储到备忘录中
memo[low][high] = result;
return result;
};
return count(1, n);
}
console.log(numTree(3));二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例 1:
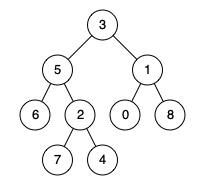
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出:3 解释:节点 5 和节点 1 的最近公共祖先是节点 3 。
// 通过递归解决(后续遍历)
function lowestCommonAncestor(root, p, q) {
// 确定递归函数
const traverse = (node, p, q) => {
// 确定递归终止条件
if (node === null || node === p || node === q) {
return node;
}
const left = traverse(node.left, p, q);
const right = traverse(node.right, p, q);
// 后续位置
// 找到一个节点,其发现p、q节点分别出现在其左右子树上
if (left !== null && right !== null) {
return node;
}
// p或q本身就是最近公共祖先
if (left === null) {
return right;
}
return left;
};
return traverse(root, p, q);
}二叉搜索树的最近公共祖先
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
示例 1:
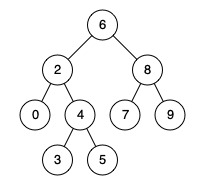
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8 输出: 6 解释: 节点 2 和节点 8 的最近公共祖先是 6。
// 因为是二叉搜索树,其是有顺序的,所以找最近公共祖先节点的问题就转换成了该节点在[p, q]中间即可
function lowestCommonAncestor(root, p, q) {
const helper = (node, p, q) => {
if (node === null) {
return node;
}
if (node.val > p.val && node.val > q.val) {
const left = helper(node.left, p, q);
if (left !== null) {
return left;
}
}
if (node.val < p.val && node.val < q.val) {
const right = helper(node.right, p, q);
if (right !== null) {
return right;
}
}
return node;
};
return helper(root, p, q);
}







































