一、图的遍历
遍历是指从某个节点出发,按照一定的的搜索路线,依次访问对数据结构中的全部节点,且每个节点仅访问一次。
前面已经讲过了二叉树的节点遍历。
类似的,图的遍历是指,从给定图中任意指定的顶点(称为初始点)出发,按照某种搜索方法沿着图的 边访问图中的所有顶点,使每个顶点仅被访问一次,这个过程称为图的遍历。遍历过程中得到的顶点序列称为图遍历序列。
图的遍历过程中,根据搜索方法的不同,又可以划分为两种搜索策略:
- 深度优先搜索
- 广度优先搜索
二、深度优先搜索(DFS,Depth First Search)
深度优先搜索,从起点出发,从规定的方向中选择其中一个不断地向前走,直到无法继续为止,然后尝 试另外一种方向,直到最后走到终点。就像走迷宫一样,尽量往深处走。
DFS 解决的是连通性的问题,即,给定两个点,一个是起始点,一个是终点,判断是不是有一条路径能 从起点连接到终点。起点和终点,也可以指的是某种起始状态和最终的状态。问题的要求并不在乎路径 是长还是短,只在乎有还是没有。
假设我们有这么一个图,里面有A、B、C、D、E、F、G、H 8 个顶点,点和点之间的联系如下图所示, 对这个图进行深度优先的遍历。
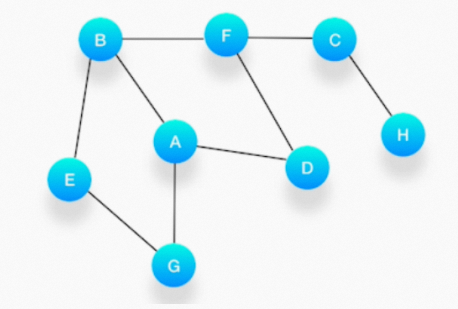
必须依赖栈(Stack),特点是后进先出(LIFO)。
第一步,选择一个起始顶点,例如从顶点 A 开始。把 A 压入栈,标记它为访问过(用红色标记),并输 出到结果中。
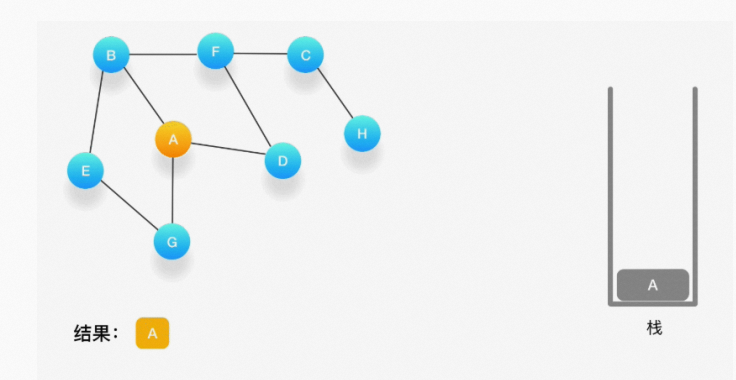
第二步,寻找与 A 相连并且还没有被访问过的顶点,顶点 A 与 B、D、G 相连,而且它们都还没有被访 问过,我们按照字母顺序处理,所以将 B 压入栈,标记它为访问过,并输出到结果中。
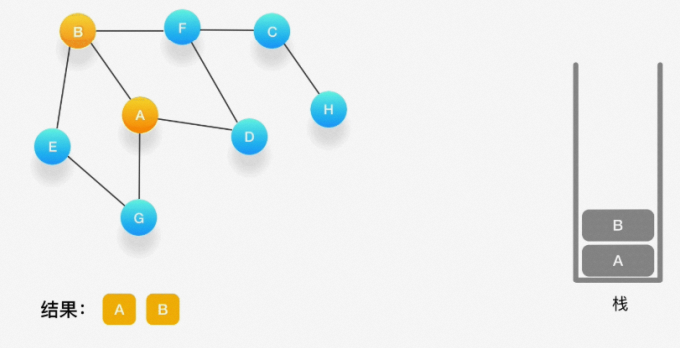
第三步,现在我们在顶点 B 上,重复上面的操作,由于 B 与 A、E、F 相连,如果按照字母顺序处理的 话,A 应该是要被访问的,但是 A 已经被访问了,所以我们访问顶点 E,将 E 压入栈,标记它为访问 过,并输出到结果中。
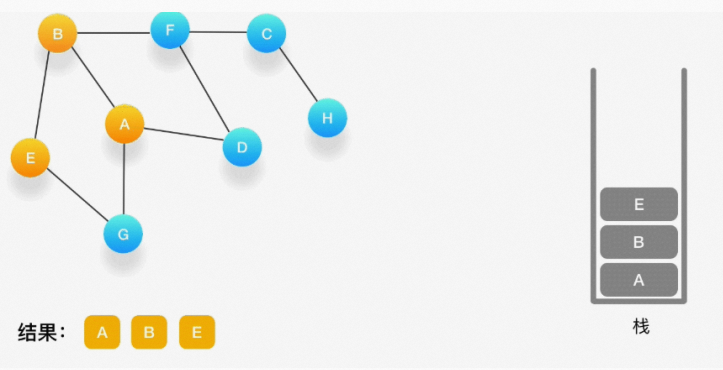
第四步,从 E 开始,E 与 B、G 相连,但是B刚刚被访问过了,所以下一个被访问的将是G,把G压入 栈,标记它为访问过,并输出到结果中。
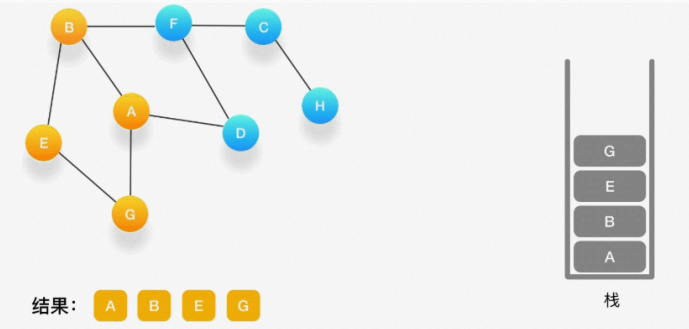
第五步,现在我们在顶点 G 的位置,由于与 G 相连的顶点都被访问过了,类似于我们走到了一个死胡 同,必须尝试其他的路口了。所以我们这里要做的就是简单地将 G 从栈里弹出,表示我们从 G 这里已 经无法继续走下去了,看看能不能从前一个路口找到出路。
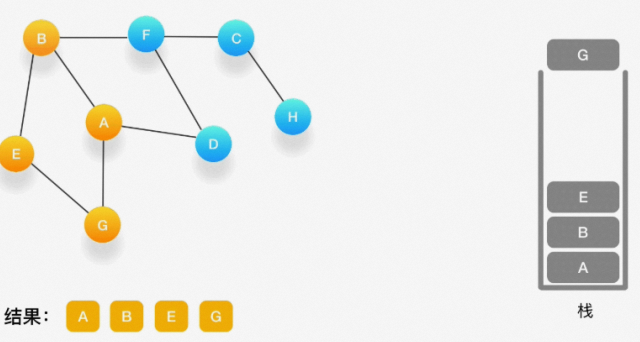
如果发现周围的顶点都被访问了,就把当前的顶点弹出。
第六步,现在栈的顶部记录的是顶点 E,我们来看看与 E 相连的顶点中有没有还没被访问到的,发现它 们都被访问了,所以把 E 也弹出去。
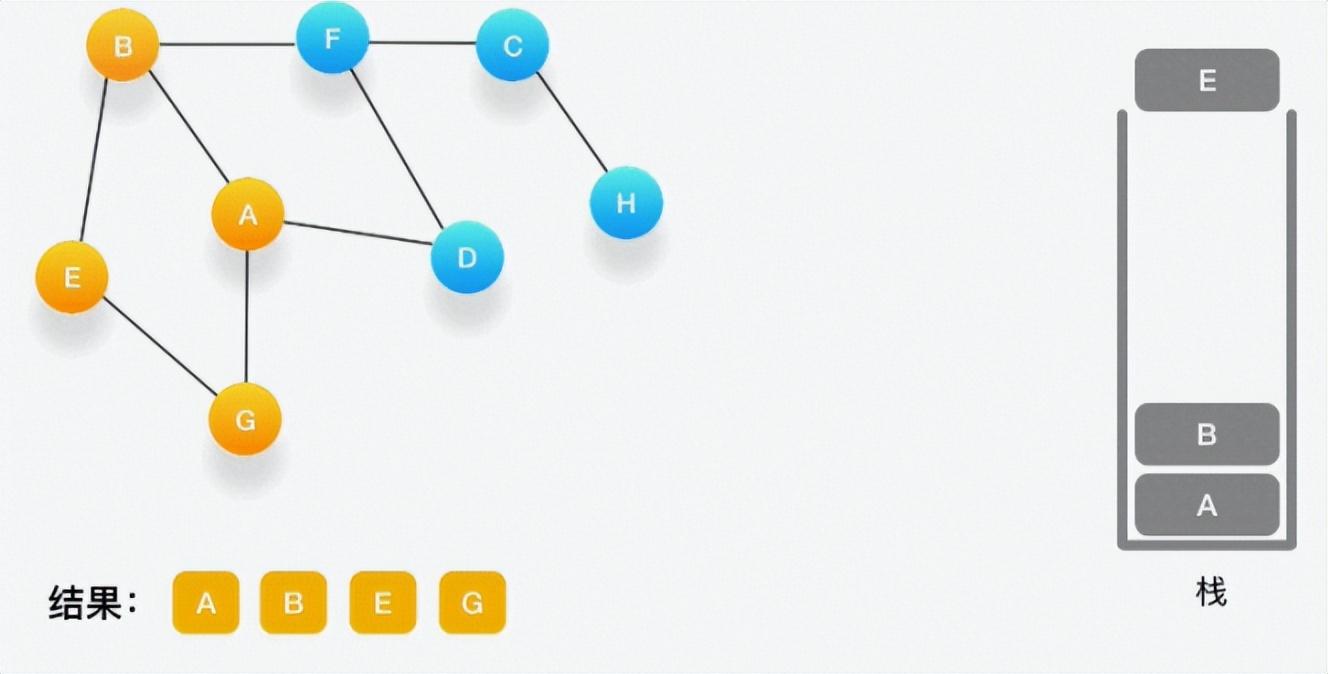
第七步,当前栈的顶点是 B,看看它周围有没有还没被访问的顶点,有,是顶点 F,于是把 F 压入栈, 标记它为访问过,并输出到结果中。
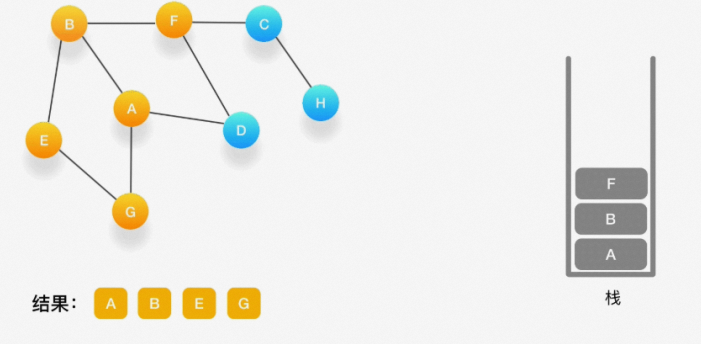
第八步,当前顶点是 F,与 F 相连并且还未被访问到的点是 C 和 D,按照字母顺序来,下一个被访问的 点是 C,将 C 压入栈,标记为访问过,输出到结果中。
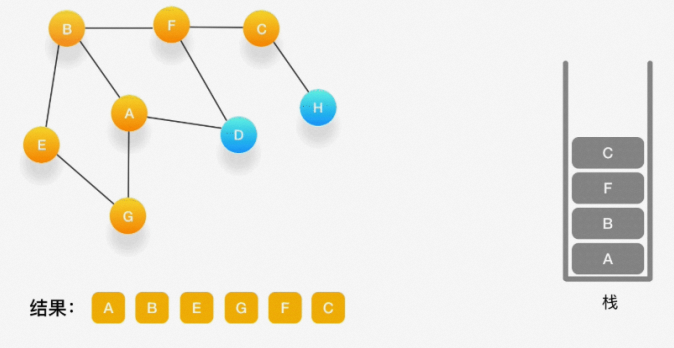
第九步,当前顶点为 C,与 C 相连并尚未被访问到的顶点是 H,将 H 压入栈,标记为访问过,输出到结 果中。
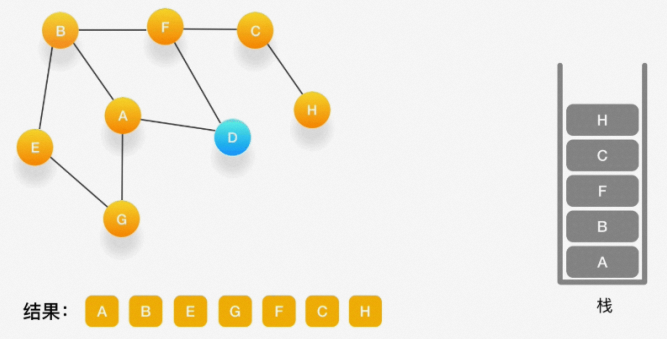
第十步,当前顶点是 H,由于和它相连的点都被访问过了,将它弹出栈。
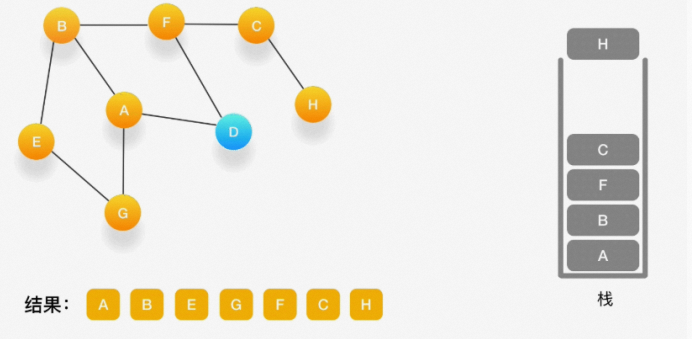
第十一步,当前顶点是 C,与 C 相连的点都被访问过了,将 C 弹出栈。
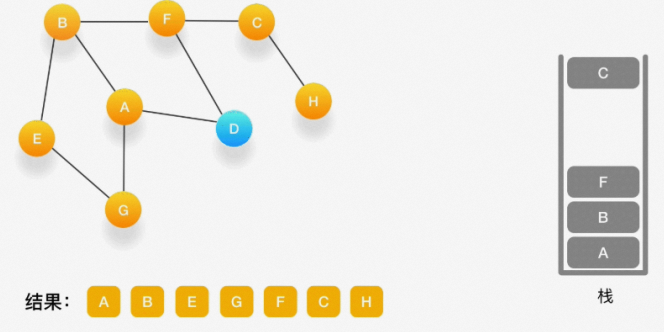
第十二步,当前顶点是 F,与 F 相连的并且尚未访问的点是 D,将 D 压入栈,输出到结果中,并标记为访问过。
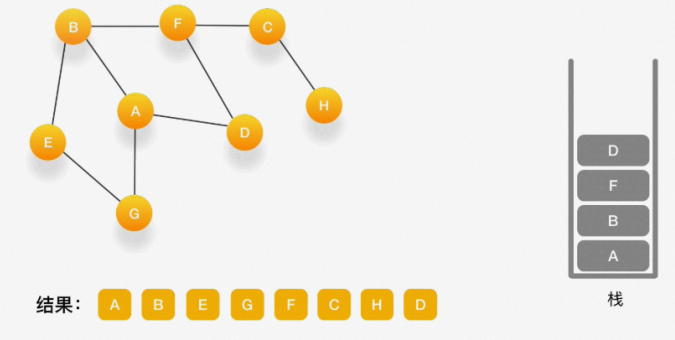
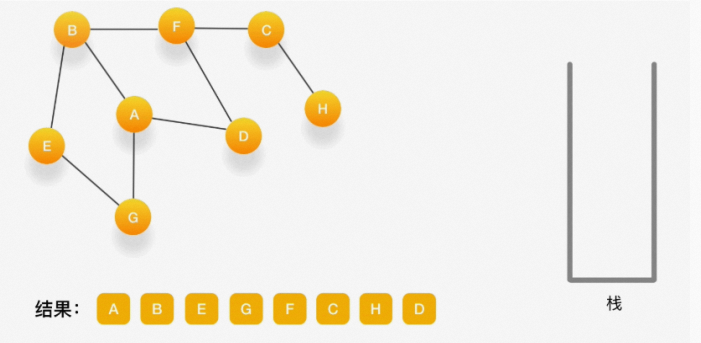
第十三步,当前顶点是 D,与它相连的点都被访问过了,将它弹出栈。以此类推,顶点 F,B,A 的邻居 都被访问过了,将它们依次弹出栈就好了。最后,当栈里已经没有顶点需要处理了,我们的整个遍历结束。
三、时间复杂度
邻接表 访问所有顶点的时间为 O(V),而查找所有顶点的邻居一共需要 O(E) 的时间,所以总的时间复杂度是 O(V + E)。
邻接矩阵 查找每个顶点的邻居需要 O(V) 的时间,所以查找整个矩阵的时候需要 O( V * V) 的时间。