数据结构与算法：图的存储

一、邻接表

用邻接矩阵来表示一个图，虽然简单、直观，但是比较浪费存储空间。

对于无向图来说，如果 A[i][j]等于 1，那 A[j][i]也肯定等于 1。实际上，我们只需要存储一个就可以了。也就是说，无向图的二维数组中，如果我们将其用对角线划分为上下两部分，那我们只需要利用上面或者下面这样一半的空间就足够了，另外一半白白浪费掉了。

还有，如果我们存储的是稀疏图（Sparse Matrix），也就是说，顶点很多，但每个顶点的边并不多，那邻接矩阵的存储方法就更加浪费空间了。比如微信有好几亿的用户，对应到图上就是好几亿的顶点。但是每个用户的好友并不会很多，一般也就三五百个而已。如果我们用邻接矩阵来存储，那绝大部分的存储空间都被浪费了针对上面邻接矩阵比较浪费内存空间的问题，我们来看另外一种图的存储方法，邻接表（Adjacency List）。

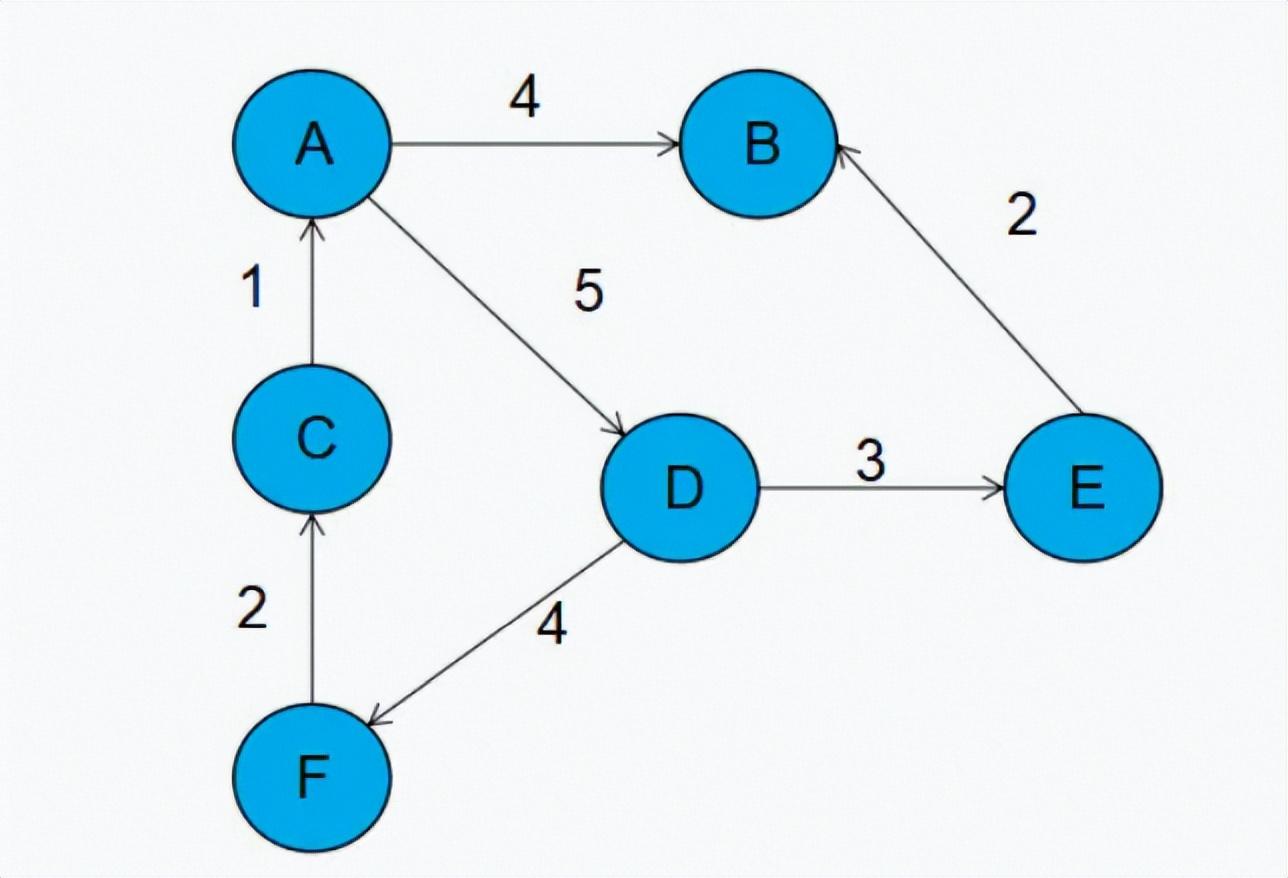
每个顶点对应一条链表，链表中存储的是与这个顶点相连接的其他顶点。

图中画的是一个有向图的邻接表存储方式，每个顶点对应的链表里面，存储的是指向的顶点。前面的数组存储的是所有的顶点，每一个顶点后面连接的块代表前面顶点所指向的顶点和路线的权值。

如果该点还指向其他顶点，则继续在块后面添加。例如A指向了B权值是4，那么A后面就加上一块，之后发现A还指向D权值是5，那么就在块尾继续添加一块。其实也就是数组+链表的结构。

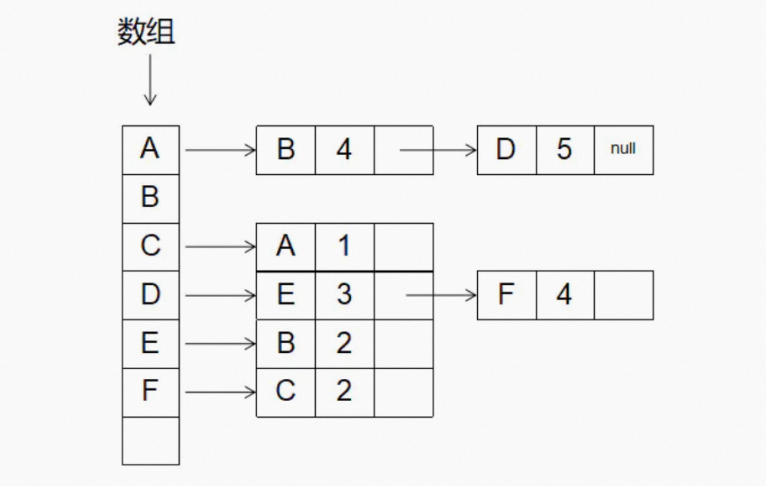
根据邻接表的结构和图，我们不难发现，图其实是由顶点和边组成的。所以我们就抽象出两种类，一个是Vertex顶点类，一个是Edge边类。

/**
 * 顶点
 */
public class Vertex {
    String name; //顶点名称
    Edge next; //从该定点出发的边
    public Vertex(String name, Edge next){
        this.name = name;
        this.next = next;
    }
}

/**
 * 边
 */
public class Edge {
    String name; //被指向的顶点
    int weight; //弧的权值
    Edge next; //被指向的下一个边
    public Edge(String name, int weight, Edge next){
        this.name = name;
        this.weight = weight;
        this.next = next;
    }
}

package graph;

import java.util.HashMap;
import java.util.Iterator;
import java.util.Map;
import java.util.Set;

/**
 * 邻接表实现
 */
public class Graph2 {
    Map<String, Vertex> vertexsMap; //存储所有的顶点
    Graph2(){
        this.vertexsMap = new HashMap<>();
    }
    public void insertVertex(String vertexName){ //添加顶点
        Vertex vertex = new Vertex(vertexName, null);
        vertexsMap.put(vertexName, vertex);
    }

    public void insertEdge(String begin, String end, int weight){
        //添加弧
        Vertex beginVertex = vertexsMap.get(begin);
        if(beginVertex == null){
            beginVertex = new Vertex(begin, null);
            vertexsMap.put(begin, beginVertex);
        }
        Edge edge = new Edge(end, weight, null);
        if(beginVertex.next == null){
            beginVertex.next = edge;
        }else{
            Edge lastEdge = beginVertex.next;
            while(lastEdge.next != null){
                lastEdge = lastEdge.next;
            }
            lastEdge.next = edge;
        }
    }

    public void print(){ //打印图
        Set<Map.Entry<String, Vertex>> set = vertexsMap.entrySet();
        Iterator<Map.Entry<String, Vertex>> iterator = set.iterator();
        while(iterator.hasNext()){
            Map.Entry<String, Vertex> entry = iterator.next();
            Vertex vertex = entry.getValue();
            Edge edge = vertex.next;
            while(edge != null){
                System.out.println(vertex.name + " 指向 " + edge.name + " 权值为：" + edge.weight);
                edge = edge.next;
            }
        }
    }

    public static void main(String[] args) {
        Graph2 graph = new Graph2();
        graph.insertVertex("A");
        graph.insertVertex("B");
        graph.insertVertex("C");
        graph.insertVertex("D");
        graph.insertVertex("E");
        graph.insertVertex("F");
        graph.insertEdge("C", "A", 1);
        graph.insertEdge("F", "C", 2);
        graph.insertEdge("A", "B", 4);
        graph.insertEdge("E", "B", 2);
        graph.insertEdge("A", "D", 5);
        graph.insertEdge("D", "F", 4);
        graph.insertEdge("D", "E", 3);
        graph.print();
    }
}

数据结构与算法：图的存储—邻接表

一、邻接表