Otsu阈值算法实战——基于Python实现图像背景分割

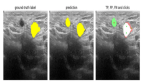
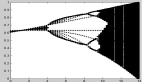
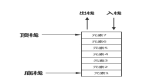
译者 | 朱先忠

审校 | 孙淑娟

让我们从一个非常技术性的概念开始。

将图像作为2D信号来浏览、分析和处理

这里有其他一些恰当的定义：

• 信号是一种随空间或时间变化的量，它可以用来传输某种形式的信息。
• 图像只不过是照射到光学系统上的光量，也就是你用来呈现它的相机或画布。

从这种意义上来说，图像只不过是一种2D信号，这种电磁信号携带了物理系统检索到的一些信息。

因此，当我们确定了图像确实是一种信号时，我们可以考虑将信号处理技术应用于图像处理任务。现在，我们可以停止哲学讨论，从具体的编码部分开始。

说到哲学，不妨让我们拍下这张照片：​

图片来源：Tingey Injury律师事务所

图片中的哲学家正在做他的工作：思考。雕塑后面是一片非常白的背景，当然我们并不在乎它。然而，我们能摆脱它吗？我们能得到这样的东西吗？

图片来源：本文作者

如果我这样问你，那就意味着我们可以。

每个略懂一些Photoshop的人都可以做到这一点，但你如何使用Python自动做到这样呢？下面我将为你展示如何做到这一点。

1.总的想法

现在，让我们来举一个简单的例子。

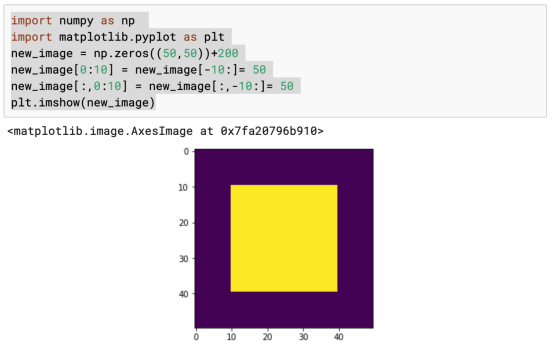
一个大正方形里面装着一个小正方形。这是一个极其简单的案例。我们要做的是将较小正方形中的所有数值设置为1，将外部的所有数值都设置为0。

我们可以使用此代码提取这两个值：

然后，做诸如以下的操作：

上述代码将图像从两个值转换为1和0。

这非常简单，对吧？下面，让我们做一点更大的尝试。

现在，我们将在较大的正方形内做一个小正方形，但两个正方形都有一些噪音数据。

new_image = np.random.normal(loc=190.0, scale=10.0, size=(50,50)).astype(int)
new_image[0:10] = new_image[-10:]=np.random.normal(loc=20.0, scale=10.0, size=(10,50)).astype(int)
new_image[:,0:10] = new_image[:,-10:]=np.random.normal(loc=20.0, scale=10.0, size=(50,10)).astype(int)
plt.imshow(new_image)

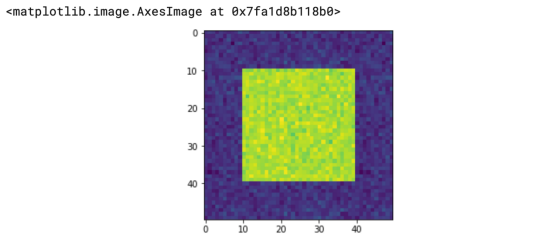
我的意思是，我们不仅有2个值，而且理论上我们还可以有0到255之间的所有值，这是这个编码中全部数值的范围。

那么，我们该怎样做呢？

我们要做的第一件事是将图像（2D信号）扁平化，并将其更改为1D信号。

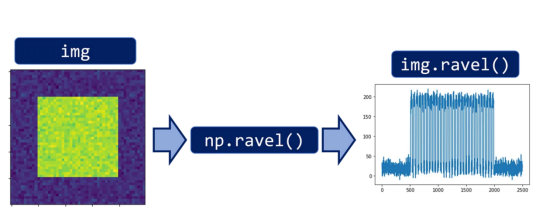
图片来源：本文作者

这张图片是一张50x50的图片，我们有了一个更加“纷乱”一些的50x50=2500长的1D信号。

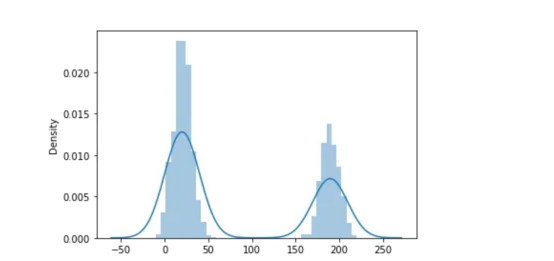
现在，如果我们研究1D信号的分布，那么，我们将会得到这样的结果：

import seaborn as sns
sns.distplot(new_image.ravel(),bins=40)

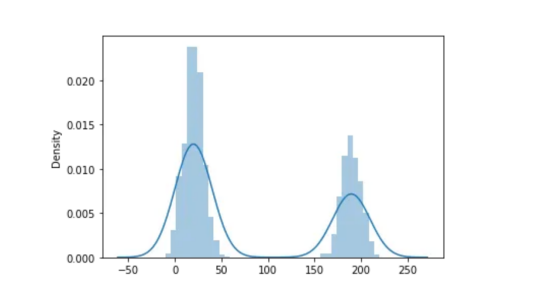
正如我们所看到的，我们有两个正态分布。这正是Otsu算法表现最好的地方。其基本思想是，图像的背景和主题具有两种不同的性质和两个不同的领域。例如，在这种情况下，第一个高斯钟形是与背景相关的钟形（假设从0到50），而第二个高斯钟形则是较小正方形（从150到250）中的一个。

所以，假设我们决定将大于100的所有值都设置为1，将小于0的所有值设置为0：​

new_image_copy = new_image.copy()
new_image[new_image<100]=0
new_image[new_image!=0]=1

这样做的结果是在背景和主体之间形成了以下遮罩：​

plt.subplot(1,2,2)
plt.imshow(new_image)
plt.subplot(1,2,1)
plt.imshow(new_image_copy)

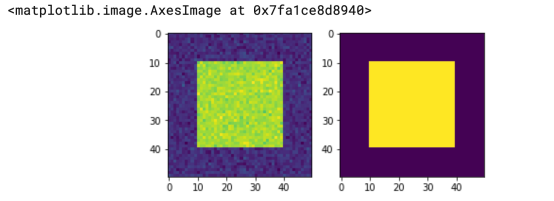
这就是Otsu算法的全部思想：

• 将图像作为2D信号导入/读取。
• 将图像展平为1D矢量。
• 选择一个阈值。
• 将低于该阈值的所有内容设置为0，将高于该阈值的全部内容设置为1。很简单，对吧？
  但是，我们如何选择合适的阈值呢？什么是最好的？让我们谈谈数学。

2.理论介绍

让我们将这个概念形式化一点。

我们在图像中有一个像素域。完整的域从0到255（白色到黑色），但不一定要那么宽（例如，可以从20到200）。

现在，多个点可以具有相同的像素强度（我们可以在同一图像中具有两个黑色像素）。假设在一个有100个像素的图像中，我们有3个强度为255的像素。现在，在该图像中具有强度255的概率是3/100。

通常，我们可以说图像中具有像素i的概率为：​

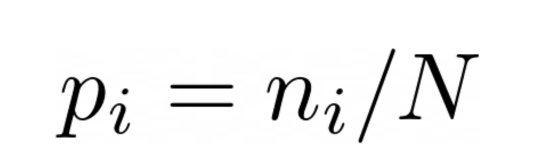
图片来源：本文作者

现在，让我们假设我们正在进行分割的像素是像素k（在我们之前的例子中，k是100）。这将对数据点进行分类。k之前的所有点属于类别0，k之后的所有点都属于类别1。

这意味着，从类别0中选择一个点的概率如下：​

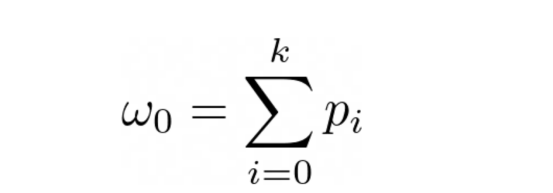
图片来源：本文作者

而从类别1中选择一个点的概率如下：​

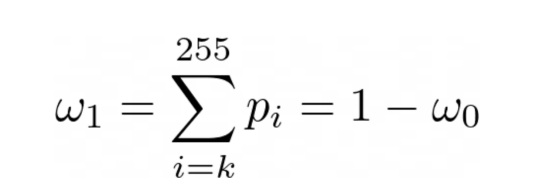
图片来源：本文作者

正如我们所看到的，这两种概率显然都依赖于k。

现在，我们可以计算的另一个值是每个类别的方差：​

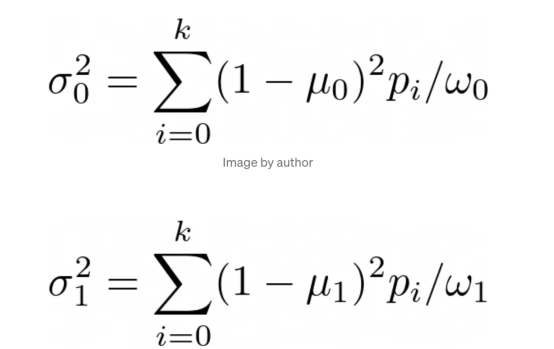
其中：​

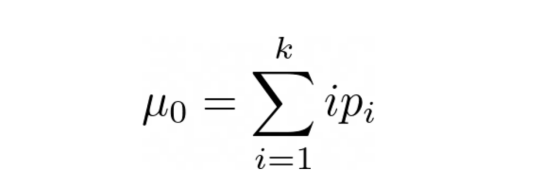
图片来源：本文作者

然后这样：

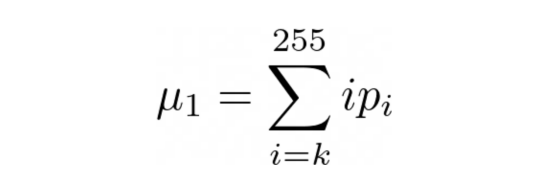
图片来源：本文作者

西格玛值是每个类别的方差，也就是该类别在mu_0和mu_1的平均值周围分布的程度。

现在，理论上的想法是找到创造我们之前在这张照片中看到的那个小山谷的值：​

但我们使用的方法略有不同，而且更加严格。通过使用线性判别分析（LDA：https://en.wikipedia.org/wiki/Linear_discriminant_analysis#Fisher's_linear_discriminant）的相同思想。在（费舍尔）LDA中，我们希望找到一个超平面，以使类别间的方差最大化（这样两个均值彼此相距最远）并且类别内的方差尽可能小（这样我们就不会在两个类别数据点之间有太多重叠）。

在这种情况下，我们没有任何超平面，而我们设置的阈值（我们的k）甚至不是一条直线，但它更像是一个我们用来区分数据点并对其进行分类的概率值。

可以证明（原始论文中提供完整的证明），在假设背景域与主题域不同的情况下，背景和主题之间的最佳分割是通过最小化此量来实现的。

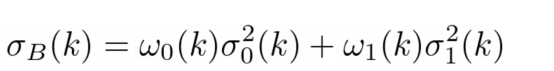
图片来源：本文作者

这意味着，我们可以尝试所有不同的k值，而且只选择k值最小的那一个。

3.编程实现

这个理论看起来可能很复杂，很难理解，但实现起来非常容易，它由三个部分组成：

3.1 导入库

我们要做的第一件事是导入我们需要的4个基本库。

import numpy as np
from PIL import Image
import matplotlib.pyplot as plt
import seaborn as sns

3.2 阈值函数

一旦你找到了完美的阈值，接下来就是如何将其应用于你的图像：

def threshold_image(im,th):
 thresholded_im = np.zeros(im.shape)
 thresholded_im[im >= th] = 1
 return thresholded_im

3.3 Otsu算法的标准

计算此数量的函数如下：

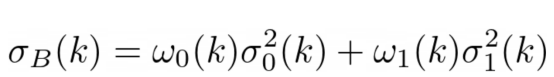
图片来源：本文作者

相关代码如下所示：

def compute_otsu_criteria(im, th):
 thresholded_im = threshold_image(im,th)
 nb_pixels = im.size
 nb_pixels1 = np.count_nonzero(thresholded_im)
 weight1 = nb_pixels1 / nb_pixels
 weight0 = 1 - weight1
 if weight1 == 0 or weight0 == 0:
 return np.inf
 val_pixels1 = im[thresholded_im == 1]
 val_pixels0 = im[thresholded_im == 0]
 var0 = np.var(val_pixels0) if len(val_pixels0) > 0 else 0
 var1 = np.var(val_pixels1) if len(val_pixels1) > 0 else 0
 return weight0 * var0 + weight1 * var1

3.4 最佳阈值计算

另一个函数只是在所有可能的ks上运行，并根据上面的标准找到最好的一个：

def find_best_threshold(im):
 threshold_range = range(np.max(im)+1)
 criterias = [compute_otsu_criteria(im, th) for th in threshold_range]
 best_threshold = threshold_range[np.argmin(criterias)]
 return best_threshold

3.5 完整的实现

因此，我们使用的是接下来的这幅图像：

图片来源：Ben Dumond on Unsplash

如果我们将该图像保存在路径中，并应用Otsu算法，我们会得到：

path_image = '/content/test_building.jpeg'
im = np.asarray(Image.open(path_image).convert('L'))
im_otsu = threshold_image(im,find_best_threshold(im))

如果我们比较im（原始图像）和im_otsu（算法之后的图像），我们得到：

plt.figure(figsize=(20,10))
plt.subplot(1,2,1)
plt.title('Original Image',fnotallow=20)
plt.imshow(im,cmap='gray')
plt.subplot(1,2,2)
plt.title('Otsu Method Image',fnotallow=20)
plt.imshow(im_otsu,cmap='gray')
plt.tight_layout()

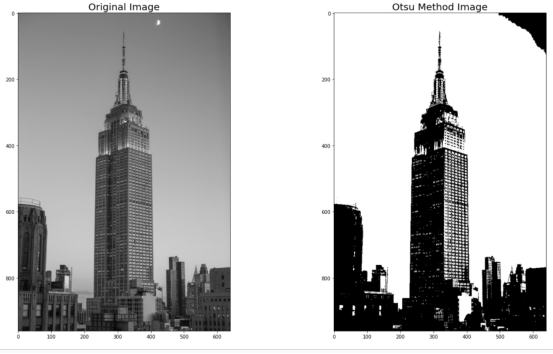
正如我们所看到的，图片右上部分的黑色部分被误解为主题，因为它与一些主题的色调相同。人并不总是完美的，算法亦然。

4.尾声

感谢您在Otsu算法教程的整个过程中一直陪伴在我身边。

在这篇简短的文章中，我们看到：

• 图像可以被视为2D信号，然后可以使用信号处理技术进行分析。
• Otsu算法的假设是，图像的背景和主题有两个连续的、不重叠的、可区分的域。
• 如何在给定Otsu算法的情况下找到图像的背景和主题之间的最佳区分。我们如何将Otsu算法解释为Fisher线性判别式。
• 如何使用Python实现Otsu算法。
• 如何在真实图像中应用此算法。

译者介绍

朱先忠，51CTO社区编辑，51CTO专家博客、讲师，潍坊一所高校计算机教师，自由编程界老兵一枚。

原文标题：​​Hands on Otsu Thresholding Algorithm for Image Background Segmentation, using Python​​，作者：Piero Paialunga