图形编辑器：排列移动功能的实现-51CTO.COM

大家好，我是前端西瓜哥。这次来讲解图形编辑器排列（arrange）功能的实现。

先看效果。

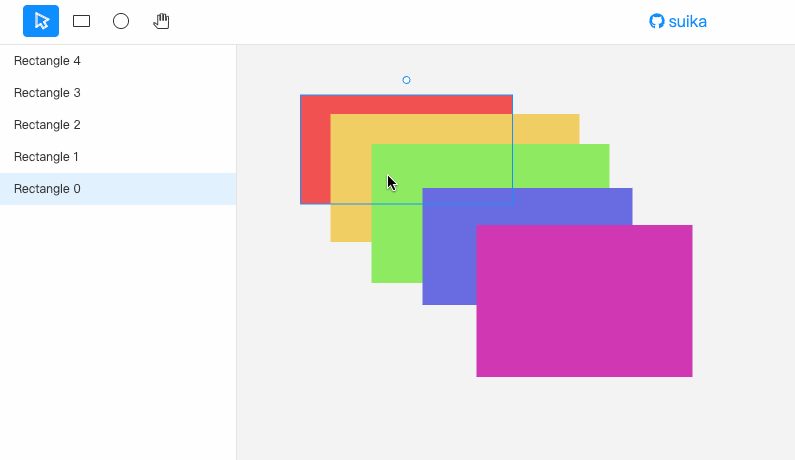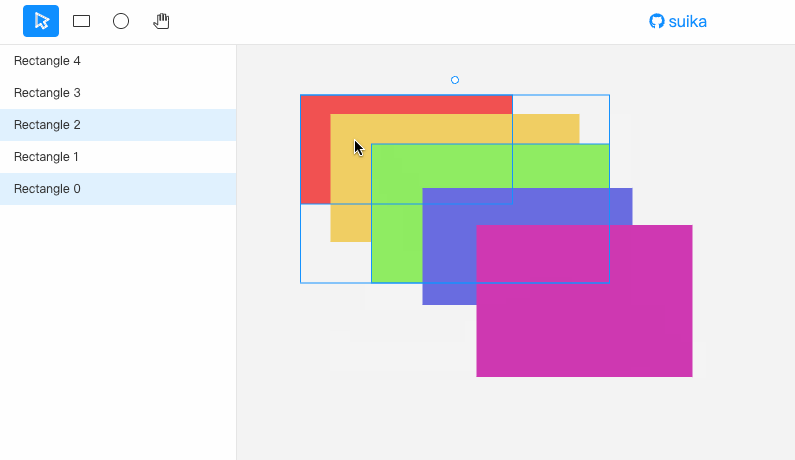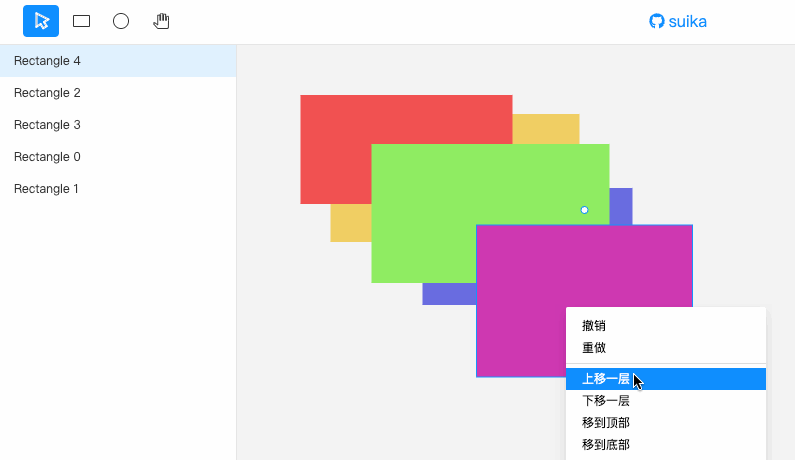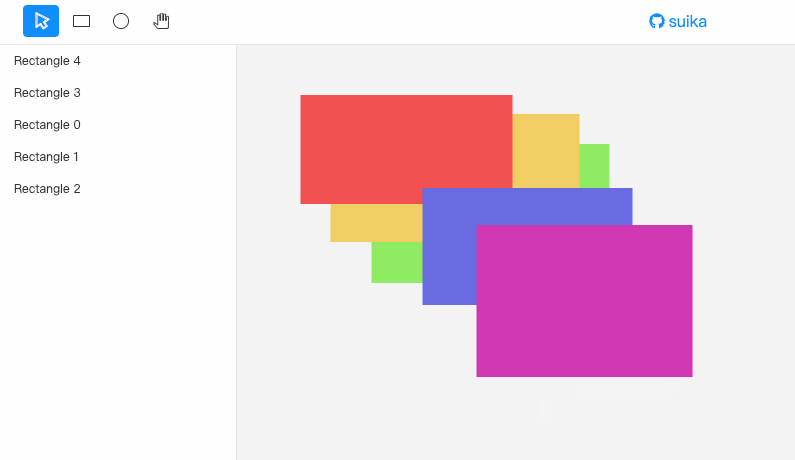
有四种移动方式：

置顶（Front）：将指定的图形移动到顶部。
置底（Back）：将制定图形移动到底部。
上移一层（Forward）：将指定元素往上移一层。
下移一层（Backward）：将置顶元素往下移动一层。

需要注意保持被移动图形，要保持它们原来的相对顺序。

编辑器 github 地址：
https://github.com/F-star/suika
线上体验：
https://blog.fstars.wang/app/suika/

Front 置顶

置顶，是将图形放在最顶部的位置。

假设图形树对应的一个数组 graphs，需要被移动的元素集合为 movedGraphSet（Set 类型）。要做的是将这些元素移动到数组末尾。

图形是按照数组的顺序绘制的，后面绘制的会盖住前面的图形，所以是移动到末尾而不是开头。这点需要注意。

我们只需要递归 graphs，不在 movedGraphSet 中的元素搬到新的数组中，在 movedGraphSet 中的元素，放到 tailGraphs 数组中。

const front = (graphs: Graph[], movedGraphSet: Set<Graph>) => {
  const newGraphs: Graph[] = [];
  const tailGraphs: Graph[] = [];
  for (let i = 0; i < graphs.length; i++) {
    const graph = graphs[i];
    if (movedGraphSet.has(graph)) {
      tailGraphs.push(graph);
    } else {
      newGraphs.push(graph);
    }
  }
  newGraphs.push(...tailGraphs);
  return newGraphs;
};

图形树可能会是链表，或者有 group 的概念，实现代码或许不同，但思路是一样的。

Back 置底

置底同理。

这次是从右往左遍历。另外因为要减少数组搬移的操作，我们需要额外将数组做一个倒序。

往数组的头部插入新元素，是要将原来的整个数组往后移动一格的，时间复杂度是 O(n)，往末尾加则不需要。

const back = (graphs: Graph[], movedGraphSet: Set<Graph>) => {
  const newGraphs: Graph[] = [];
  const tailGraphs: Graph[] = [];
  for (let i = graphs.length - 1; i >= 0; i--) {
    const graph = graphs[i];
    if (movedGraphSet.has(graph)) {
      tailGraphs.push(graph);
    } else {
      newGraphs.push(graph);
    }
  }
  newGraphs.push(...tailGraphs);
  return newGraphs.reverse(); // 反向
};

Forward 上移一层

将存在于 movedGraphSet 的图形都往后移动一个位置。需要注意多个需要移动的图形如果紧邻，是要将它们作为一个整体放到它们之后的第一个不移动图形的后面的。

比如被操作数组为 [0, 1, 2, 3, 4, 5, 6, 7]，指定数组元素为 [1, 2, 6]，返回 [0, 3, 1, 2, 4, 5, 7, 6]。

一开始我想的从左往右遍历，用多个指针记录连续需要移动的图形的，然后发现实现上也太复杂了吧。要维护指针，还要判断指针什么时候应该移动什么的。

后面我换了个思路，改为从右往左遍历。如果当前元素是需搬移元素，就和下一个元素交换。

这样，一个不用搬移的元素就能往前挤过被搬运元素的集群。

const forward = (graphs: Graph[], movedGraphs: Set<Graph>) => {
  const newGraphs = [...graphs];
  for (let i = newGraphs.length - 2; i >= 0; i--) {
    if (movedGraphs.has(newGraphs[i])) {
      // 交换
      [newGraphs[i], newGraphs[i + 1]] = [newGraphs[i + 1], newGraphs[i]];
    }
  }
  return newGraphs;
};

Backward 下移一层

同理。

换个方向。

const backward = (graphs: Graph[], movedGraphs: Set<Graph>) => {
  const newGraphs = [...graphs];
  for (let i = 1; i < newGraphs.length; i++) {
    if (movedGraphs.has(newGraphs[i])) {
      [newGraphs[i], newGraphs[i - 1]] = [newGraphs[i - 1], newGraphs[i]];
    }
  }
  return newGraphs;
};