红黑树插入有五种情况,每种情况对应着不同的调整方法:
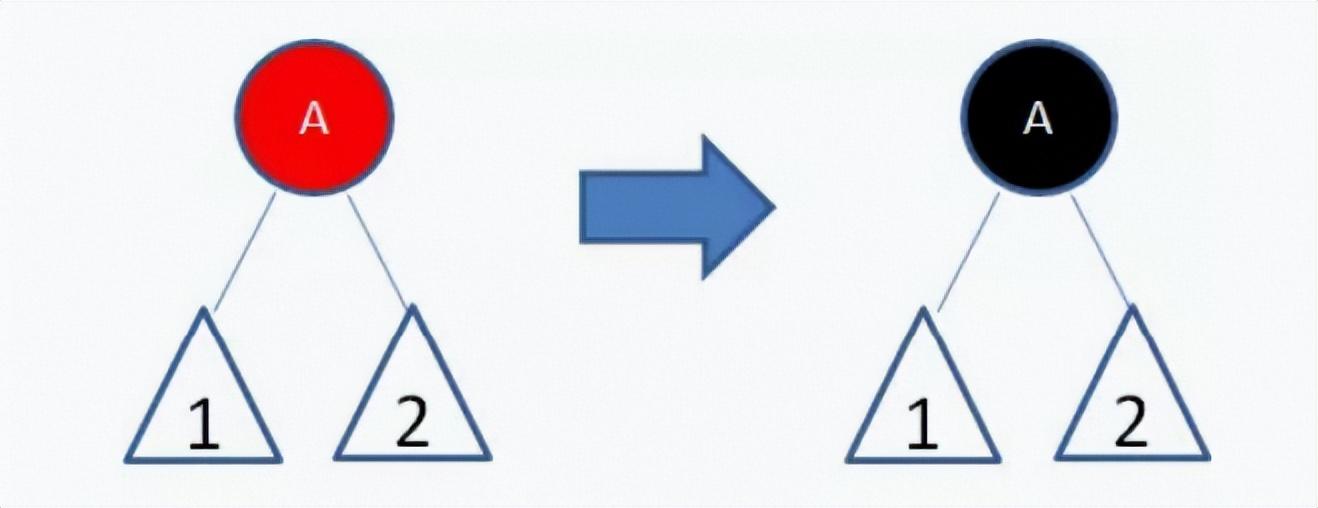
一、 新结点(A)位于树根,没有父结点。
直接让新结点变色为黑色,规则2得到满足。同时,黑色的根结点使得每条路径上的黑色结点数目 都增加了1,所以并没有打破规则5。
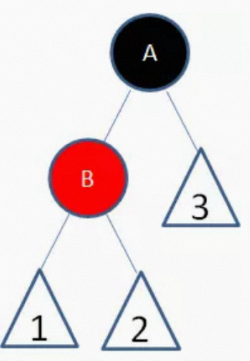
二、 新结点(B)的父结点是黑色
新插入的红色结点B并没有打破红黑树的规则,所以不需要做任何调整
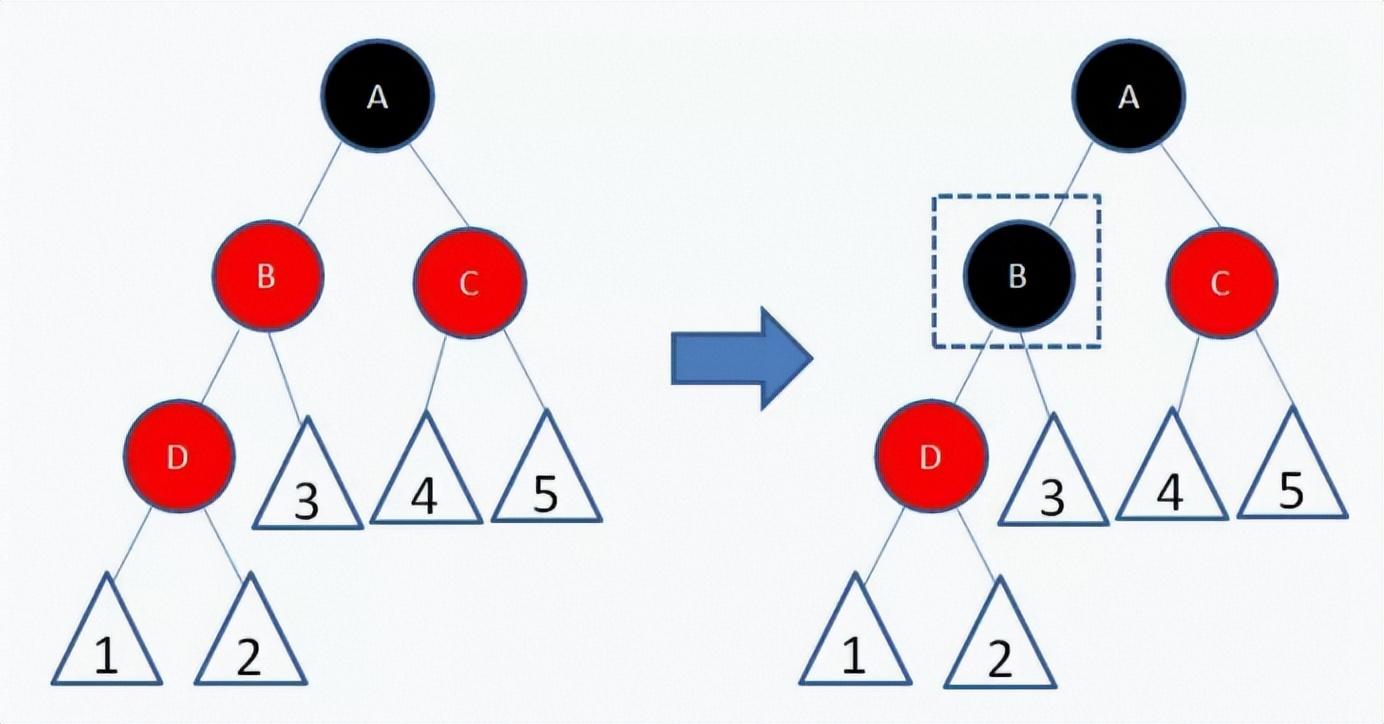
三、 新结点(D)的父结点和叔叔结点都是红色
两个红色结点B和D连续,违反了规则4。因此我们先让结点B变为黑色。
这样一来,结点B所在路径凭空多了一个黑色结点,打破了规则5。因此我们让结点A变为红色
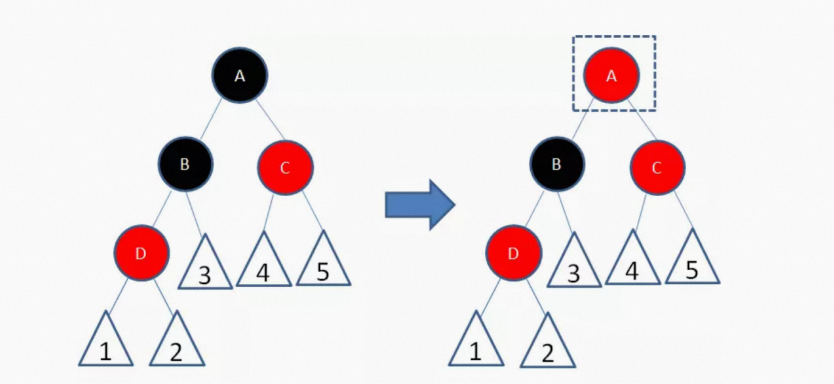
结点A和C又成为了连续的红色结点,我们再让结点C变为黑色
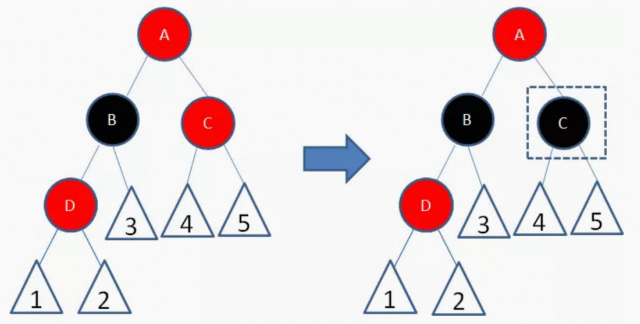
四、 新结点(D)的父结点是红色,叔叔结点是黑色或者没有叔叔,且新结点是父结点的右孩子,父结 点(B)是祖父结点的左孩子
我们以结点B为轴,做一次左旋转,使得新结点D成为父结点,原来的父结点B成为D的左孩子
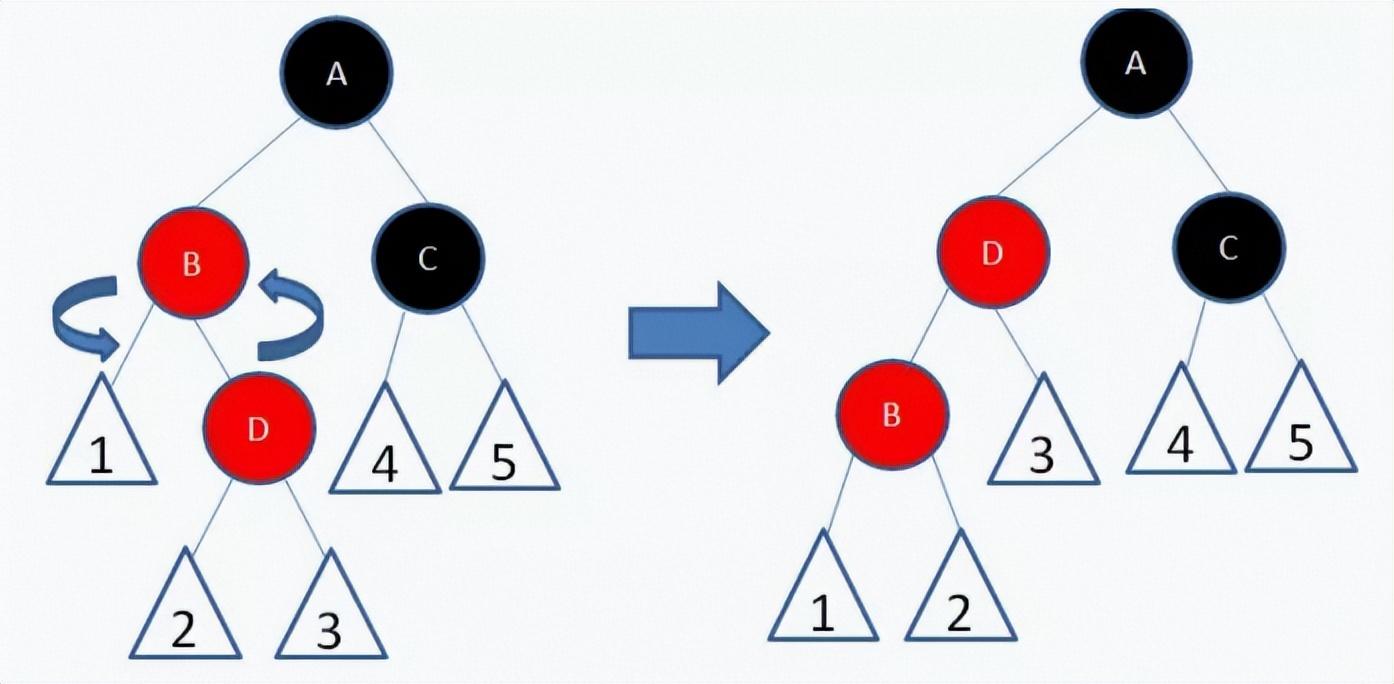
这样进入了情况5。
五、新结点(D)的父结点是红色,叔叔结点是黑色或者没有叔叔,且新结点是父结点的左孩子,父结 点(B)是祖父结点的左孩子
我们以结点A为轴,做一次右旋转,使得结点B成为祖父结点,结点A成为结点B的右孩子
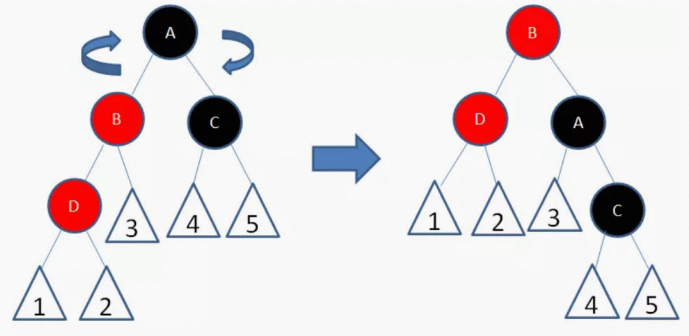
接下来,我们让结点B变为黑色,结点A变为红色。
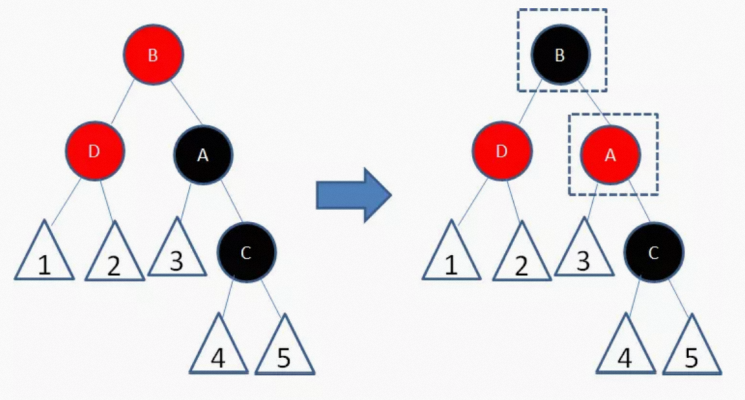
经过上面的调整,这一局部重新符合了红黑树的规则。




































