时间序列特征提取的Python和Pandas代码示例-51CTO.COM

使用Pandas和Python从时间序列数据中提取有意义的特征，包括移动平均，自相关和傅里叶变换。

前言

时间序列分析是理解和预测各个行业(如金融、经济、医疗保健等)趋势的强大工具。特征提取是这一过程中的关键步骤，它涉及将原始数据转换为有意义的特征，可用于训练模型进行预测和分析。在本文中，我们将探索使用Python和Pandas的时间序列特征提取技术。

在深入研究特征提取之前，让我们简要回顾一下时间序列数据。时间序列数据是按时间顺序索引的数据点序列。时间序列数据的例子包括股票价格、温度测量和交通数据。时间序列数据可以是单变量，也可以是多变量。单变量时间序列数据只有一个变量，而多变量时间序列数据有多个变量。

有各种各样的特征提取技术可以用于时间序列分析。在本文中，我们将介绍以下技术:

Resampling
Moving Average
Exponential Smoothing
Autocorrelation
Fourier Transform

1、Resampling

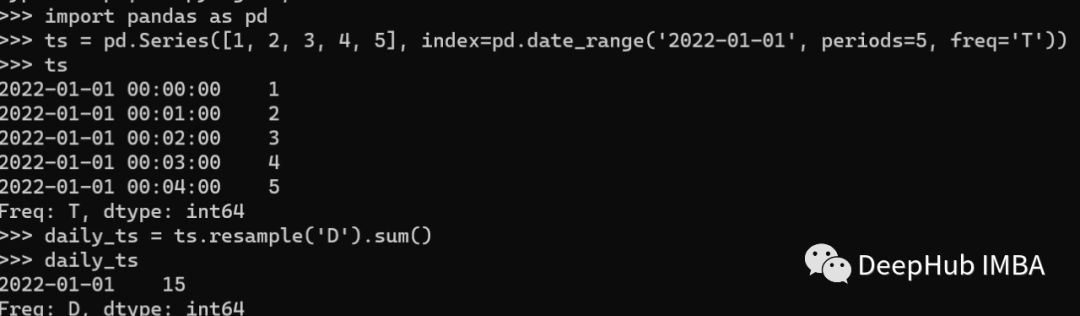
Resampling 重采样主要是改变时间序列数据的频率。这对于平滑噪声或将数据采样到较低的频率很有用。Pandas提供了resample()方法对时间序列数据进行重新采样。resample()方法可用于对数据进行上采样或下采样。下面是一个如何将时间序列降采样到每日频率的示例:

import pandas as pd
 
 # create a time series with minute frequency
 ts = pd.Series([1, 2, 3, 4, 5], index=pd.date_range('2022-01-01', periods=5, freq='T'))
 
 # downsample to daily frequency
 daily_ts = ts.resample('D').sum()
 
 print(daily_ts)

在上面的例子中，我们创建了一个以分钟为频率的时间序列，然后使用resample()方法将其采样到每天的频率。

2、Moving Average

Moving Average 移动平均是一种通过在滚动窗口上求平均值来平滑时间序列数据的技术。可以帮助去除噪声并得到数据的趋势。Pandas提供了rolling()方法来计算时间序列的平均值。下面是一个如何计算时间序列的平均值的例子:

import pandas as pd
 
 # create a time series
 ts = pd.Series([1, 2, 3, 4, 5])
 
 # calculate the rolling mean with a window size of 3
 rolling_mean = ts.rolling(window=3).mean()
 
 print(rolling_mean)

我们创建了一个时间序列，然后使用rolling()方法计算窗口大小为3的移动平均值。

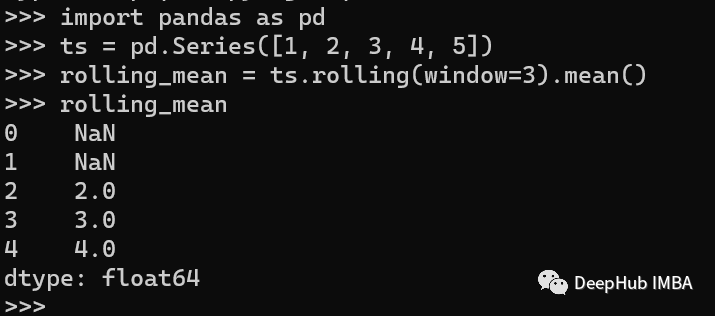
可以看到前两个值因为没有到达移动平均的最小数量3，所以会产生NAN，如果需要的话可以再使用fillna方法进行填充。

3、Exponential Smoothing

Exponential Smoothing 指数平滑是一种通过赋予最近值更多权重来平滑时间序列数据的技术。它可以帮助去除噪声获得数据的趋势。Pandas提供了计算指数移动平均的ewm()方法。

import pandas as pd
 ts = pd.Series([1, 2, 3, 4, 5])
 ts.ewm( alpha =0.5).mean()

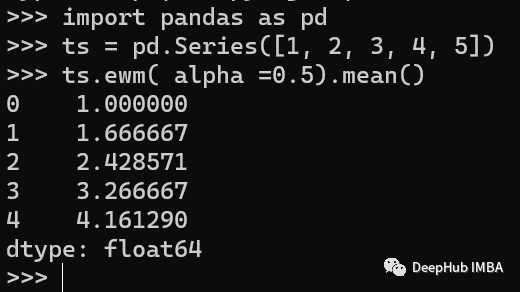
在上面的例子中，我们创建了一个时间序列，然后使用ewm()方法计算平滑因子为0.5的指数移动平均。

ewm有很多的参数，这里我们介绍几个主要的。

com：根据质心指定衰减

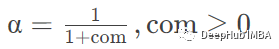
span 根据范围指定衰减

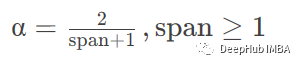
halflife 根据半衰期指定衰减

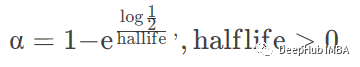
alpha 指定平滑系数α

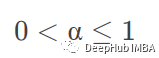
以上4个参数都是指定平滑系数α，只是前三个是根据条件计算出来的，最后一个是手动指定，所以至少要有一个，例如上面的例子我们就直接手动设定了0.5

min_periods 窗口中具有值的最小观察数，默认 0。

adjust 是否进行误差修正默认True。

adjust =Ture时公式如下：

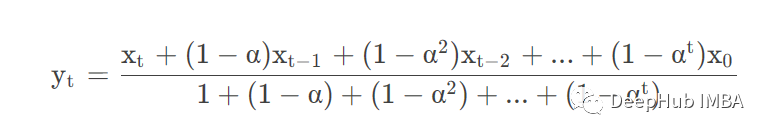
adjust =False

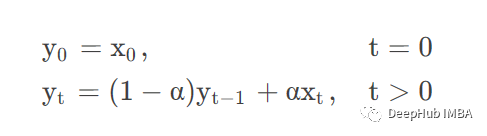
4、Autocorrelation

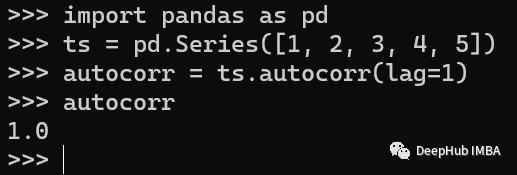
Autocorrelation 自相关是一种用于测量时间序列与其滞后版本之间相关性的技术。可以识别数据中重复的模式。Pandas提供了autocorr()方法来计算自相关性。

import pandas as pd
 
 # create a time series
 ts = pd.Series([1, 2, 3, 4, 5])
 
 # calculate the autocorrelation with a lag of 1
 autocorr = ts.autocorr(lag=1)
 
 print(autocorr)

5、Fourier Transform

Fourier Transform 傅里叶变换是一种将时间序列数据从时域变换到频域的技术。可以识别数据中的周期性模式。我们可以使用numpy的fft()方法来计算时间序列的快速傅里叶变换。

import pandas as pd
 import numpy as np
 
 # create a time series
 ts = pd.Series([1, 2, 3, 4, 5])
 
 # calculate the Fourier transform
 fft = pd.Series(np.fft.fft(ts).real)
 
 print(fft)

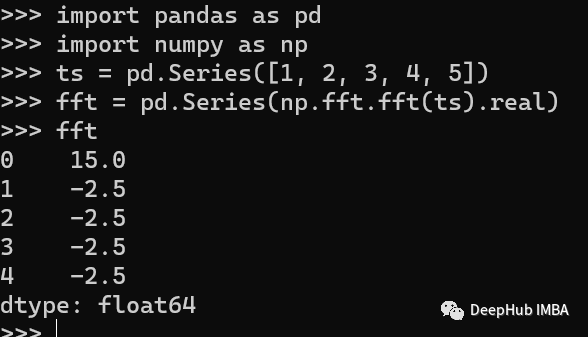
这里我们只显示了实数的部分。

总结

在本文中，我们介绍了几种使用Python和Pandas的时间序列特征提取技术。这些技术可以帮助将原始时间序列数据转换为可用于分析和预测的有意义的特征，在训练机器学习模型时，这些特征都可以当作额外的数据输入到模型中，可以增加模型的预测能力。