几何算法：矩形碰撞和包含检测算法-51CTO.COM

大家好，我是前端西瓜哥。今天来讲讲几何算法中，比较经典的算法：矩形碰撞和包含检测算法。

矩形碰撞检测是被广泛使用的算法。

比如在游戏中，为了优化图形碰撞判断效率（复杂不规则图形之间的碰撞算法很复杂），经常会使用到包围盒。

所谓包围盒子是一个矩形，通常正好包围住一个规则或不规则的图形。如果两个图形的包围盒没有发生碰撞，那这两个图形一定不会发生碰撞，因为矩形的碰撞算法很简单，所以能够很好地优化性能。

算法实现

考虑到有些读者对原理不感兴趣，想赶紧找到算法复制粘贴，很急，我这里先直接贴上代码实现。

判断矩形是否碰撞：

function isRectIntersect(rect1, rect2) {
  return (
    rect1.x <= rect2.x + rect2.width &&
    rect1.x + rect1.width >= rect2.x &&
    rect1.y <= rect2.y + rect2.height &&
    rect1.y + rect1.height >= rect2.y
  );
}

判断矩形 1 是否包含矩形 2：

function isRectContain(rect1, rect2) {
  return (
    rect1.x <= rect2.x &&
    rect1.x + rect1.width >= rect2.x + rect2.width &&
    rect1.y <= rect2.y &&
    rect1.y + rect1.height >= rect2.y + rect2.height
  );
}

矩形碰撞检测原理

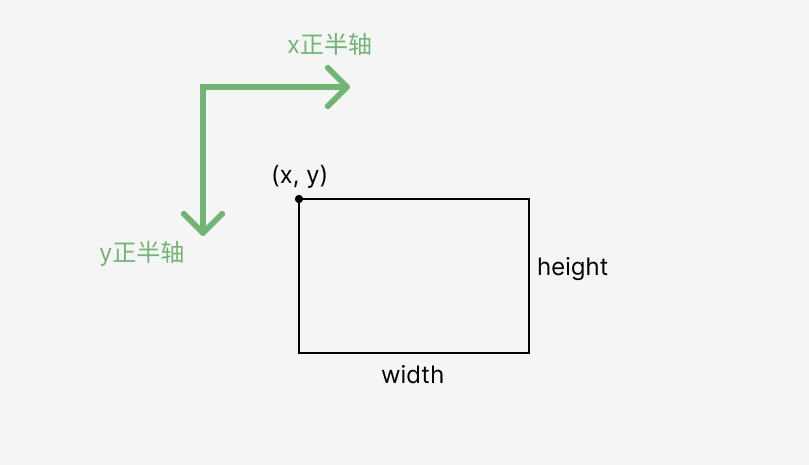
首先明确矩形的定义。我们用 4 个属性来描述一个矩形，分别为 x、y、width、height，表示矩形的左上角位置和尺寸。

这里用主流的坐标系统表示，以屏幕左上角为原点，x轴正方向向右，y 轴正方形向下。

或者我们可以用 minX、minY、maxX，minY 来表示：

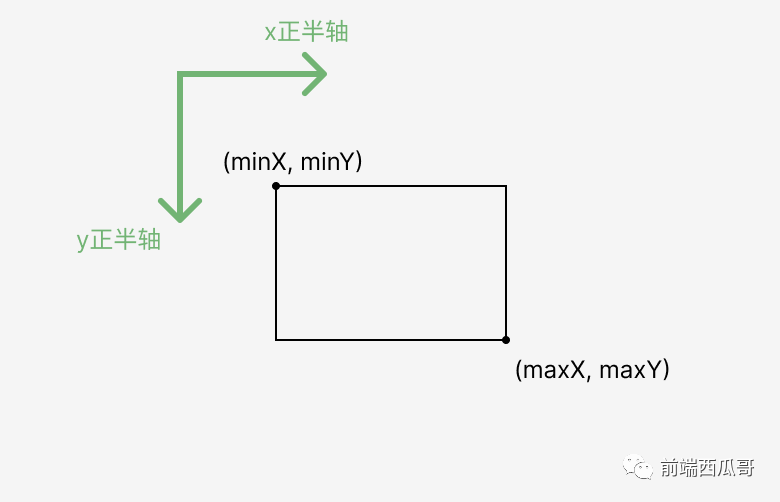
矩形碰撞，也叫矩形相交。矩形发生碰撞的条件是：两个矩形有重叠的区域。

下图是两个矩形碰撞的一些情况：

先看 x 维度，将两个矩形往 x 轴线上投影，我们得到两条线段。

矩形要相交，首先 x 的范围上就应该有交集，等价于判断两个线段是否有交点。

先看看什么情况下它们不会相交？答案是：一条线段的右端点在另一条线的的左端点的左侧。

所以相交的逻辑是：

!(rect1.x > rect2.x + rect2.width || rect1.x + rect1.width < rect2.x)

转换一下，就是：

rect1.x <= rect2.x + rect2.width &&
rect1.x + rect1.width >= rect2.x

y 维度同理，为：

rect1.y <= rect2.y + rect2.height &&
rect1.y + rect1.height >= rect2.y

所以最终算法实现为：

function isRectIntersect(rect1: IRect, rect2: IRect) {
  return (
    rect1.x <= rect2.x + rect2.width && // minX1 <maxX
    rect1.x + rect1.width >= rect2.x &&
    rect1.y <= rect2.y + rect2.height &&
    rect1.y + rect1.height >= rect2.y
  );
}

矩形包含原理

思路类似矩形碰撞。

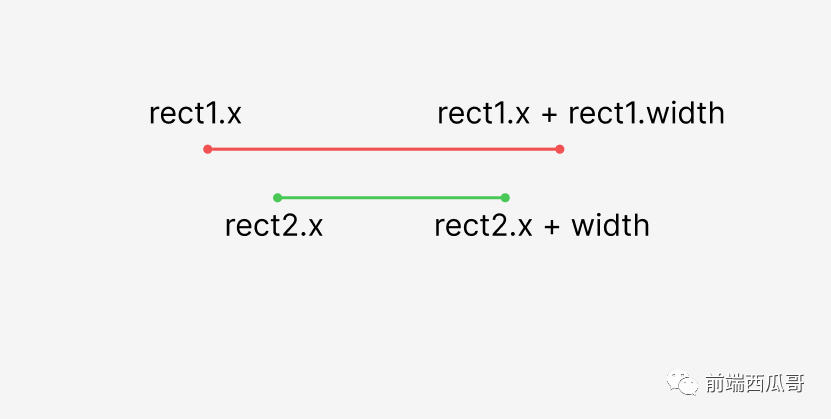
也是判断两条线段的位置关系，rect 1 包含 rect 2，首先在 x 维度上需要满足 rect 2 的两个点都在 rect 1 的 x 范围内。

代码为：

rect1.x <= rect2.x &&
rect1.x + rect1.width >= rect2.x + rect2.width

y 同理，最终代码实现为：

function isRectContain(rect1, rect2) {
  return (
    rect1.x <= rect2.x &&
    rect1.x + rect1.width >= rect2.x + rect2.width &&
    rect1.y <= rect2.y &&
    rect1.y + rect1.height >= rect2.y + rect2.height
  );
}

结尾

矩形算法的碰撞和包含算法，思路是降低维度，分解为判断线段的相交关系。