1.什么是 AB 实验?
AB 实验是为了验证某一个产品能力或者策略的好坏,制作两个(A/B)或多个(A/B/n)版本,在同一时间维度,分别让组成成分相同(相似)的访客群组(目标人群)随机的访问这些版本,收集各群组的用户体验数据和业务数据,并且结合统计学原理,分析评估出最好版本正式采用。
通过 AB 实验前置的验证收益,使决策有据可依。同时也可以利用 AB 实验分流出小部分流量进行测试,防止错误决策对整体用户产生负面影响。
2 为什么要引入 AB 实验
价格系统作为基础的公共服务,是需要满足各业务方的不同应用场景下的报价需求,提供不同场景下不同类型的报价能力。
同时,我们会针对各自的需求,去选择合适的报价方式,制定不同的报价策略,当市场价格出现变动,业务需求或目标及运营策略发生改变时,我们也需要进行调整,这种调整可能是策略上的调整、报价方选择的调整、算法模型的调整;也可能是新增报价策略、报价方式或引入新的算法模型。
但价格对于各使用业务方来说大多数情况下是敏感的,有些调整和改变,我们事先是不能够明确知道,到底能不能给业务带来正向的收益或达到预期的目标及效果,也很有可能出现未预知的负面结果。
所以我们不能全部简单粗暴的进行大规模的应用,而是需要建立在数据基础上的思维方式,通过数据反馈会告诉我们做出的决策好不好,哪里有问题,以及衡量可以带来多少确定性的增长。
而 A/B-test 正是我们进行决策验证的一个“利器”。
另外从产品研发流程来看,基于 AB 实验的研发流程相比传统产品的研发流程,其优势也是全方位的。

3 如何进行 AB 实验
A/B 实验可以看作一个“无尽”的学习环,不断的通过业务驱动做迭代,数据驱动做决策。通过提出假设、定义成功指标、检验假设(A/B 实验)、分析学习、发布、建立另一个假设,这就形成一个完整的闭环,通过多轮实验迭代,使策略趋于更优。
A/B 实验流程:

3.1 提出假设
实验的第一步就是明确实验需求产生的背景以及实验目标,即我们希望借助实验验证什么猜想假设达到什么样的目标,并且我们需要从用户角度以及数据角度去论证假设的结果。
这里我们需要先对总体均值提出一个假设,然后用样本信息去检验这个假设是否成立。我们把提出的这个假设叫做原假设,与原假设对立的结论叫做备择假设,如果原假设不成立,就要拒绝原假设,进而接受备择假设。
3.2 定义评价指标
评价指标是用于评估实验结果的各项指标数据,因为实验的效果主要是通过实验指标来判断的,所以对于评价指标的一个基本要求就是,评价指标要能反映实验者的意图,并且可测、易测。
在选取指标时,从指标重要程度来看,指标可以分为主要指标、次要指标和护栏指标三类:
主要指标:需要优化的目标指标,决定这个实验的最终发展方向,主要由实验的目标来选择;
次要指标:次要指标可以从多个角度反映实验策略的效果,辅助进行全量决策。
护栏指标:用于辅助保障 A/B 测试的质量,衡量 A/B 测试是否符合业务上的长期目标,不会因为优化短 期指标而打乱长期目标,防止发生“捡芝麻掉西瓜”的情况。
3.3 实验设计
3.3.1 选取实验单位
首先要知道分流指的是我们直接将整体流量切割为几块,每个流量只能在一个实验中。AB 实验的核心思想在于寻找两组同质且与大盘类似的小流量对象群体,通过观察不同策略在这两组同质对象群体上的表现,来预估策略应用到全量后的效果。
因此,如何合理的分流找到这样的对象群体,则成为了影响 AB 实验评估准确性的关键因素。
这里需要注意分流对象与随机单元,分流对象是需要根据核心指标来确定的根据什么来进行分流;随机单元就是 AB 实验要达到随机的最小单元。
3.3.2 计算样本量
从理论上讲,样本量越多越好,因为当样本数量很少的时候,实验容易被新的样本点带偏,造成了实验结果不稳定,难以得出确信的结论。相反的,样本数量变多,实验说服性也更强。但是在现实操作中,样本量应该越少越好,这是因为:
流量有限:大公司因为用户数量足够多,同时跑几十个甚至上百个实验也没问题。但小公司流量有限,还要持续对产品进行迭代。在保证不同实验的样本不重叠的情况下,产品迭代的速度会大大降低。
试错成本大:如果使用 50%的流量进行实验,一周后结果表明实验组的总收入下降了 20%。算下来,实验在一周内给整个公司带来了 10%的损失。试错成本太高。
在计算样本量时有两种情况,一种是均值,一种是比率,两种情况计算方式有所差异:
均值:

比率:

我们根据自己有的数据带入公式就能计算出所需样本量了。
3.3.3 流量分割
确定好实验流量之后,就可以制定分流策略将实验流量划分到对照组和不同的实验组中
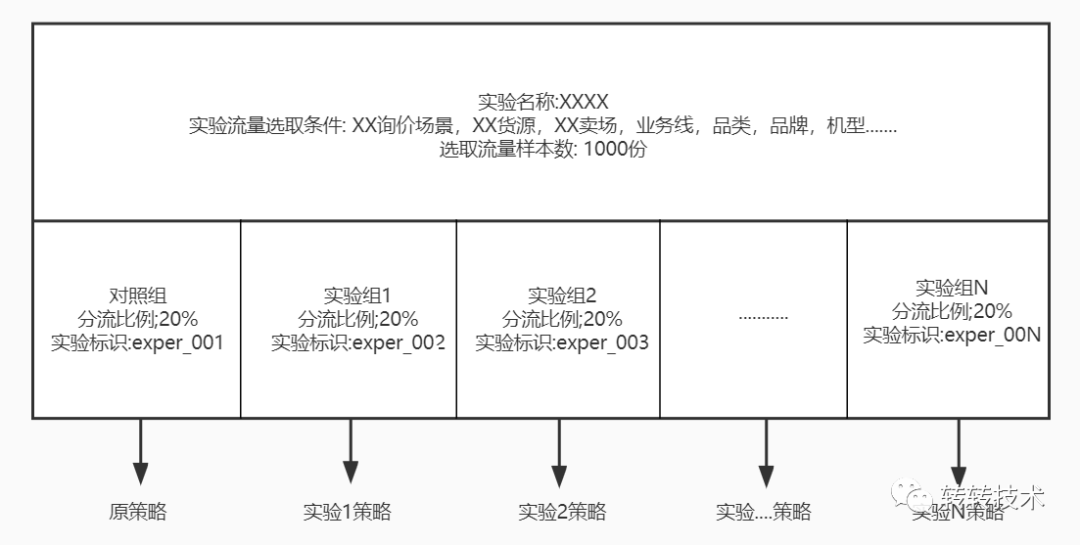
确保在实验前分出无差别的实验组和对照组,避免因流量分配不平衡导致的 AB 群组差异过大,最终造成对于实验结果的误判,在进行 AB 实验之前我们需要保证实验的分流是均匀的,一般实践中,主要采取 AA 空跑的方式来验证:
AA 空跑:针对选定的实验组和对照组,在上实验策略前先空跑一段时间。如果空跑期的样本量和各项指标均无显著差异,则认为实验分流是均匀的。这种方式的缺点是需要空跑期,会延长实验所需时间。(分流也可以前置在随机分流时观测两组历史数据的差异,差异大建议重新分流)
3.3.4 实验周期计算
实验周期的设定是个权衡的问题,一方面,我们希望有足够多的流量,保证实验策略可以充分体现出来;另一方面,也希望缩短实验周期、提升迭代效率、降低实验风险。
在评估周期的时候,有两点需要格外注意!!!
其一:周期效应。考虑到用户在周中和周末的表现存在差异,因此实验周期最好跨越一周,消除不同时间周期实验效果的不同。
其二:新奇效应。策略的调整对于用户而言,是从陌生到熟悉的过程,而在陌生阶段,往往会有一些不真实的表现,因此最好等实验指标趋于平稳之后再进行评估。
4 进行分流实验埋点上报
进行实验分流阶段其实就是按照事先设计好的实验计划进行线上执行,但需要注意的是需要验证实验进行是否符合预期的设定。
实验过程中会将实验标识标记到每个实验流量请求的日志中用于记录,然后数据计算系统根据带有实验标记的日志计算用户的各种实验数据指标,最终用于产出分析报表。
如发现实验过程中出现异常情况应及时预警进行处理或回退。
5 实验结果分析(假设验证)并决策
实验结束后,我们基于实验样本进行数据统计,进而验证实验前假设的正确性,我们得出这一有效结论的科学依据便是假设检验。
假设检验是利用样本统计量估计总体参数的方法; 对于原假设提出的命题,我们需要作出判断,要么原假设成立,要么原假设不成立。因为基于样本对总体的推断,会面临着犯两种错误的可能:第一类错误,原假设为真,我们却拒绝了;第二类错误,原假设为伪,我们却接受了。
显然,我们希望犯这两类错误的概率越小越好,但对于一定的样本量 n,不能同时做到犯这两类错误的概率很小。
在假设检验中,就有一个对两类错误进行控制的问题。一般来说,哪一类错误所带来的后果严重、危害越大,在假设检验中就应该把哪一类错误作为首要的控制目标。
在假设检验中,我们都执行这样一个原则,首先控制犯第一类错误的概率。这也是为什么我们在实际应用中会把要推翻的假设作为原假设,这样得出的结论更具说服力(我们有足够充分的证据证明原来确定的结论是错误的),所以通常会看到,我们把要证明的结论作为备择假设。
5.1 T检验
常见的假设检验方法有 Z 检验、T 检验和卡方检验等,不同的方法有不同的适用条件和检验目标。
Z 检验和 T 检验都是用来推断两个总体均值差异的显著性水平,具体选择哪种检验由样本量的大小、总体的方差是否已知决定。
在样本量较小且总体的方差未知的情况下,这时只能使用样本方差代替总体方差,样本统计量服从 T 分布,应该采用 T 统计量进行检验。T 统计量具体构造公式如下图所示,其中 f 是 T 统计量的自由度,S1、S2 是样本标准差。

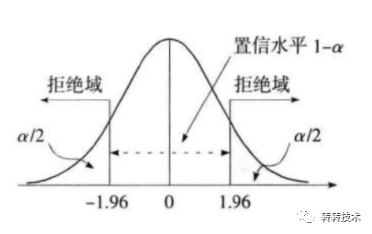
T 检验的流程是,在给定的弃真错误概率下(一般取 0.05),依据样本统计量 T 是否落在拒绝域来判断接受还是拒绝原假设。实际上在确定弃真错误概率以后,拒绝域的位置也就相应地确定了。
使用 T 统计量进行判断的好处是,进行决策的界限清晰,但缺陷是决策面临的风险是笼统的。
例如 T=3 落入拒绝域,我们拒绝原假设,犯弃真错误的概率为 0.05;T=2 也落入拒绝域,我们拒绝原假设,犯弃真错误的概率也是 0.05。
事实上,依据不同的统计量进行决策,面临的风险也是有差别的。为了精确地反映决策的风险度,我们仍然需要 P 值来帮助业务来做决策。
5.2 利用 P 值决策
P 值是当原假设为真时,所得到的样本观察结果或更极端的结果出现的概率。如果 P 值很小,说明这种情况发生的概率很小,但是在这次试验中却出现了,根据小概率原理,我们有理由拒绝原假设,P 值越小,我们拒绝原假设的理由越充分。
P 值可以理解为犯弃真错误的概率,在确定的显著性水平下(一般取 0.05),P 值小于显著性水平,则拒绝原假设。
5.3 基于假设验证的科学评估
围绕着科学评估要解决的两个问题,实验前,针对圈定的流量使用假设检验,通过 AA 实验确保分出无差别的实验组和对照组;
实验后,基于实验前选定的用于验证假设结论的指标,构造 T 统计量并计算其对应的 P 值,依据 P 值帮我们做决策。
5.4 决策
实验结果分析,假设验证后就进入了决策阶段,根据实验分析结果决定是否继续优化实验策略再次实验或终止实验或进入实验放量阶段。
如果进入实验放量阶段,需要综合考虑三个因素:效率、质量、风险。对于一个实验,我们希望在评估正向的前提下,尽快上线。但往往由于策略 bug、新功能不符合预期、用户体感不好等问题,使得在放量阶段需要更加的谨慎,以下为一个标准的放量流程:
第一阶段:小流量阶段
此阶段衔接在小流量评估后,整体放量比例控制在(5%)以下,评估实验是否对指标有负向影响。同时验证策略的触发,以及排查是否存在潜在风险。在无风险的前提下,一般建议持续 3-5 日左右,进入下一个阶段。
第二阶段:放量阶段
这个阶段,随着样本量的逐渐放开,实验的结果也会更加精准;与此同时,伴随而来可能会出现流量压力等问题的发生,因此在此阶段需要跟进放量,观察是否有出现问题。逐级放量建议持续至少一周,以观测周中和周末的影响。
第三阶段:长期存放阶段
针对部分实验,如果希望长期观测实验效果,可以保留 5%以下的原始策略,作为「反转桶」。
6 总结
AB测试不能解决所有的问题,但是仍然不失为衡量线上优化迭代的最有效方式之一。可衡量的实验目标、有效的实验分流、实验结果的正确解读是AB测试成功的关键。
关于作者:王梦龙,转转研发技术部软件工程师































