本文经AI新媒体量子位(公众号ID:QbitAI)授权转载,转载请联系出处。
随着光学算法发展,如今我们用低维传感器也能“捕获”高维信号了。
举个例子,这是我们用2D传感器拍到的一张“照片”,看起来充满了噪声数据:

然而,正是通过这张“照片”所包含的数据,我们就能还原出一段动态的视频来!

听起来很神奇,但通过一种名叫快照压缩成像(Snapshot Compressive Imaging, SCI)的方法,确实能实现。
这种方法能将高维数据作为二维测量进行采样, 从而实现高效地获取高维视觉信号。
以相机为例,虽然它是2D传感器,但如果想办法在相机镜头后加个数字微镜器件测量设备 (Digital Micromirror Devices,DMD,这是一种能精确地控制光源的器件),就有办法使普通的相机对高维数据进行降维测量,得到简易的的2D数据,再还原出高维3D的视觉信号。
比如,普通的相机帧率很低,一秒最多只能拍几十张照片(假设能拍30张)。
当我们想拍摄高速运动的物体时,只要给普通相机加上这个数字微镜器件,它就会沿时间维度压缩视频信号,每拍到一张照片就能还原出来几帧甚至几十帧照片(也就是还原出来一段视频)。
假设我们给数字微镜器件预设的压缩率是10,那么,现在拍一张照片就能还原出来10张照片(或者说是一段包含了10帧照片的视频),而相机的帧率也直接翻了10倍,变成一秒能拍300张照片。
现在问题来了,要如何从这些含有噪声的压缩低维测量数据中,尽可能高效地恢复原始高维信号呢?
随着深度学习发展,各种重建算法也都被提了出来,然而这些算法重建信号的准确性和稳定性仍然不够好。
为此,来自港大、中科院和西湖大学的研究人员,提出了一种用于视频快照压缩成像的Deep Equilibrium Models(DEQ)方法,目前已被AAAI 2023收录:

这种方法不仅提升了重建准确度和稳定性,还进一步优化了内存占用空间——
算法在训练和测试中只需要常数级内存,即:在使用深度学习时,它所消耗的内存空间不随网络深度变化(而在使用传统优化方法时,它所消耗的内存空间不随迭代次数变化)。
一起来看看。
快照压缩成像难点是什么?
受益于新颖光学硬件和成像算法的设计,快照压缩成像(Snapshot Compressive Imaging, SCI)系统可以在一次快照测量中,将高维数据作为二维测量进行采样, 从而实现高效地获取高维视觉信号。
如图1所示,SCI系统可以分为两个部分,硬件编码和软件解码:
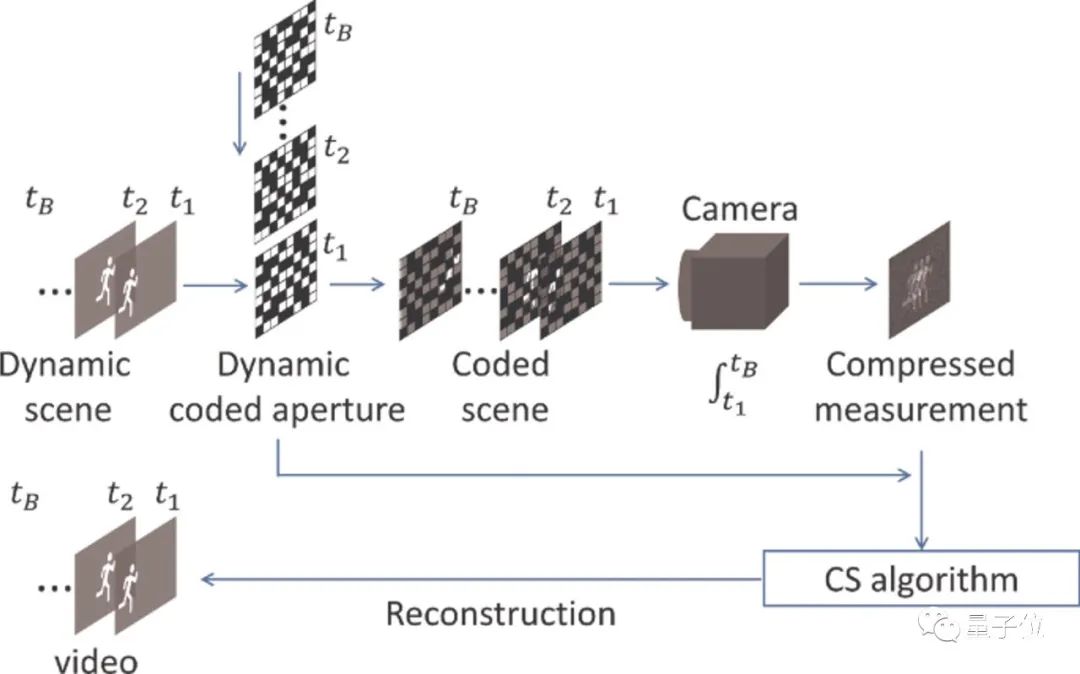
△图1. 快照压缩成像系统使用低维传感器在快照测量中捕获高维数据
以拍摄视频为例,通过硬件编码,SCI系统对视频数据进行采样,在时间维度上压缩;此后,采用算法来重建原始的高维视频数据。
这里考虑视频SCI系统,如视频1所示,视频上半部分展示的是SCI系统硬件部分得到的压缩测量,视频下半部分是使用该论文提出的算法恢复出来的视频结果。
显然,整个成像过程中需要求解一个逆问题:如何从含噪声的压缩测量中恢复视频。
尽管目前已经有很多重建方法可以求解SCI成像的逆问题,但这些方法各有缺陷,如图2所示:
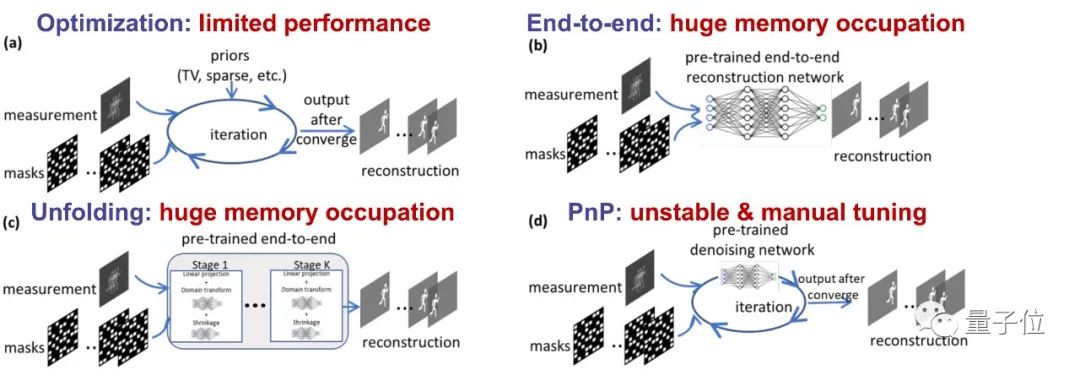
△图2. SCI重建的现有方法和主要问题
其中,传统的优化算法(a)性能有限。
而随着深度学习的发展,端到端的深度网络(b)和unfolding方法(c)虽然能提高性能,但不可避免地随着层网络深度的增加而遭受不断增长的内存占用需求,并且需要精心地设计模型。
即插即用(PnP)框架(d)虽然享受数据驱动正则化和灵活迭代优化的优点,但是这种算法必须通过适当的参数设置来保证准确的结果,甚至需要采用一些复杂的策略来获得令人满意的性能。
相比于其他方法,论文提出了新算法DE-RNN和DE-GAP,来保证重建结果的准确性和稳定性,其重建结果的性能可以收敛到一个较高水平,如图3所示:
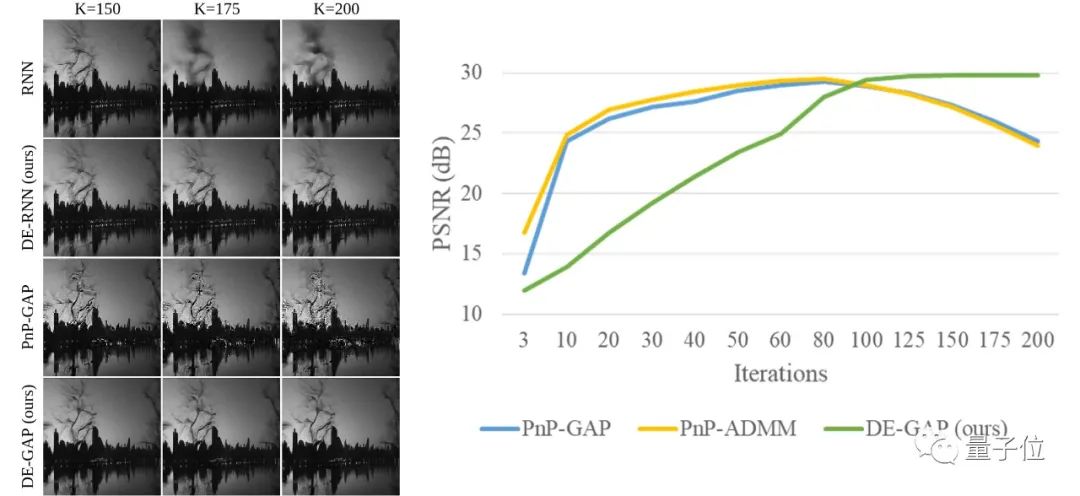
△图3. DE-GAP与其他方法重建结果对比
通常来说,以往方法如RNN和PnP的重建结果不稳定,甚至在长期迭代中性能变差。
但DE-GAP重建结果却能随着迭代次数的增加保持性能的提升,并最终收敛到稳定的结果。
这是怎么做到的?
引入先进模型提升性能
为了解决以往方法存在的问题、实现更先进的SCI重建,这篇论文首次提出了一种新思路——
使用DEQ模型,解决视频SCI重建的逆问题。
DEQ模型在2019年被首次提出,主要应用于自然语言处理中的大规模长序列语言处理任务。
如图4所示,DEQ模型可以通过牛顿迭代法等求根方法,在前向传播和反向传播的过程中直接求解出不动点,从而仅使用常数级内存就等效实现了无穷深网络:
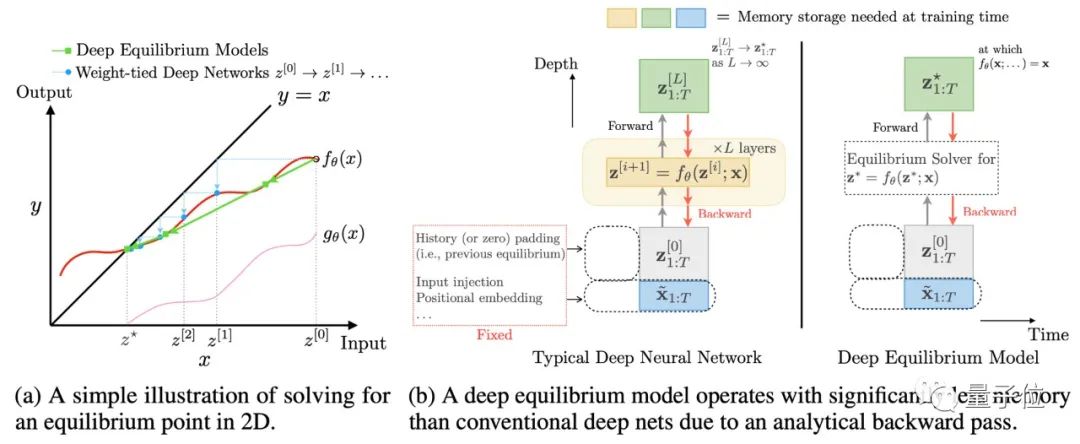
△图4. DEQ模型的求解不动点方法(左)和常数级内存占用(右)
(图4出自论文:S. Bai et al, “Deep equilibrium models”, NeurIPS 2019.)
具体来说,这篇论文首次将DEQ模型应用于两个现有的视频SCI重建框架:RNN和PnP。
效果也非常不错,RNN相当于仅使用常数级内存实现了无穷深网络,PnP等效于实现了无穷多迭代优化步骤,并且在迭代优化过程中直接求解不动点。
如图5所示,论文为RNN和PnP分别设计了结合DEQ模型的迭代函数,这里x是重建结果,y是压缩测量,Φ是测量矩阵:
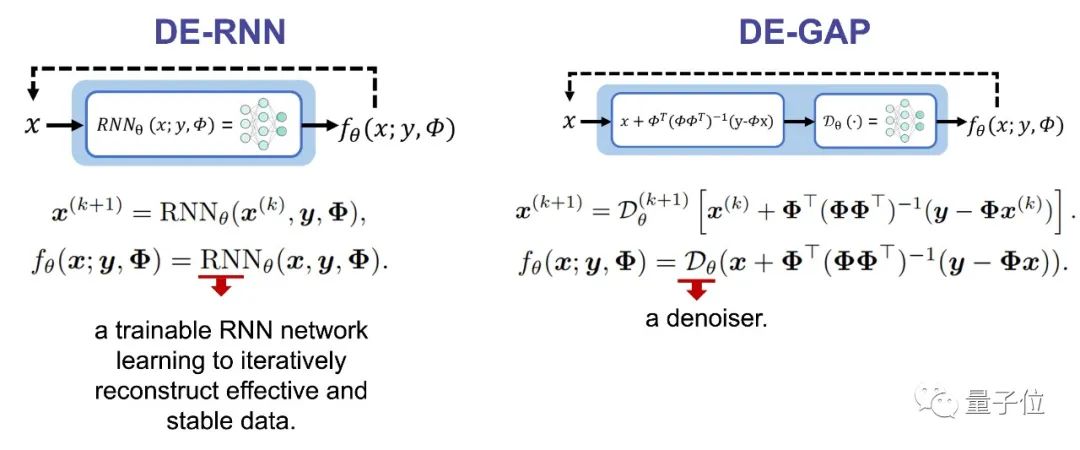
△图5. RNN和PnP分别结合DEQ模型后的迭代函数
(具体推导过程和前后向传播的细节请见论文)
实验结果如何?
论文在六个经典的SCI数据集和真实数据上都进行了实验,相较以往的方法,整体重建结果都要更好。
如表1显示,平均而言,这种方法在PSNR实现了大约0.1dB的改善,SSIM实现了大约0.04的改善。SSIM的改进表明,这种方法可以重建具有相对精细结构的图像:
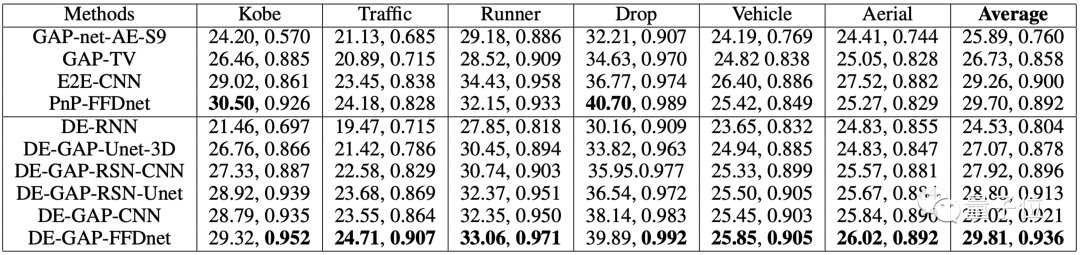
△表1. 视频SCI重建的六个经典数据集上不同算法的PSNR(dB)和SSIM
图6则是经典数据集上不同算法的重建结果对比,在一些细节的呈现上更加流畅清晰:

△图6
图7则是真实数据上不同算法的重建结果对比,效果相比之下也要更好:
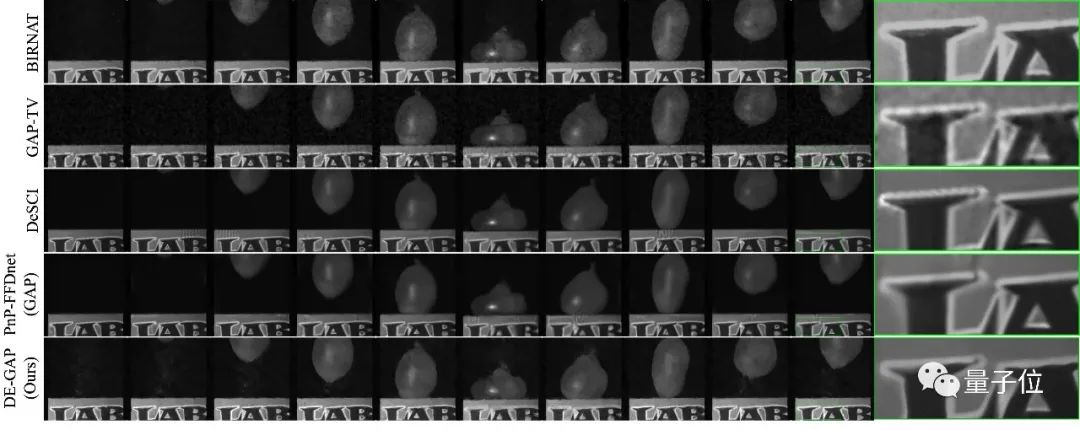
△图7
更多实验结果可见论文。
目前论文代码已开源,感兴趣的小伙伴们可以用起来了~
(文末还附上了作者的讲解视频,深入浅出)
论文地址:
https://arxiv.org/pdf/2201.06931
代码地址:
https://github.com/IndigoPurple/DEQSCI
论文讲解视频by作者:
英语:https://www.bilibili.com/video/BV1X54y1g7D9/
中文:https://www.bilibili.com/video/BV1V54y137QK/
塑料粤语:https://www.bilibili.com/video/BV1224y1G7ee/