超越Transformers——基于PyNeuraLogic的神经符号编程

译者 | 朱先忠​

审校 | 孙淑娟​

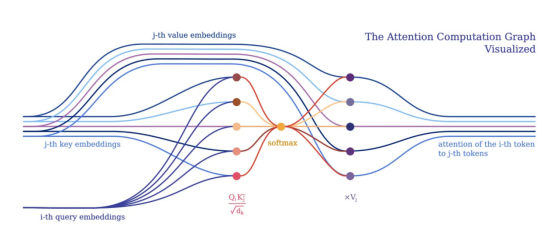
从令牌角度的注意力计算图可视化（注意令牌间的关系）​

在过去几年中，我们看到了不少基于Transformer的模型的兴起（引文1），并在许多领域得到成功的应用，如自然语言处理或计算机视觉等。在本文中，我们将探索一种简洁、可解释和可扩展的方式，将深度学习模型（特别是Transformer）表达为混合架构，即通过将深度学习与符号人工智能相结合。为此，我们将使用一个名为PyNeuraLogic的基于Python语言的神经符号框架中实现模型设计。​

【注意】本文作者也是​​PyNeuraLogic框架​​的设计者之一。

“如果没有混合架构、丰富的先验知识和复杂的推理技术这三大要素，我们就无法以充分、自动化的方式构建丰富的认知模型。”（引文2）​

-加里·马库斯（新硅谷机器人创业公司Robust.AI首席执行官兼创始人）​

将符号表示与深度学习相结合，填补了当前深度学习模型中的空白，例如开箱即用的可解释性或缺少推理技术等。也许，提高参数的数量并不是实现这些理想结果的最佳方法，就像增加相机百万像素的数量不一定会产生更好的照片一样。​

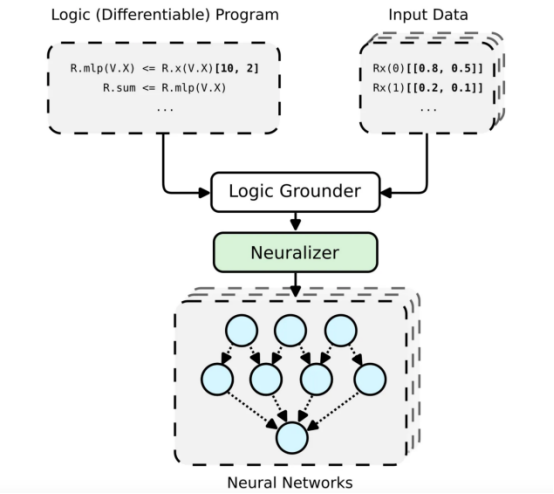
PyNeuraLogic框架工作流总体架构​

神经符号概念的高级可视化提升关系神经网络（LRNN，见引文3），这可以借助（Py）NeuraLogic实现。这里我们展示了一个简单的模板（逻辑程序）——通过一个线性层后面跟着一个求和聚合。对于每个（输入）样本，构建一个独特的神经网络。​

PyNeuraLogic框架是基于特别设计的逻辑编程（逻辑程序中包含可微参数）实现的。该框架非常适合于较小的结构化数据（如分子）和复杂模型（如Transformers和图形神经网络）。但是，另一方面需要注意的是，PyNeuraLogic不是非关系型和大张量数据的最佳选择。​

框架的关键组成部分是一个可微逻辑程序，我们称之为模板。模板由以抽象方式定义神经网络结构的逻辑规则组成，我们可以将模板视为模型架构的蓝图。然后，将模板应用于每个输入数据实例以产生（通过接地和神经化）输入样本特有的神经网络。这个过程与其他具有预定义架构的框架完全不同，预定义架构无法根据不同的输入样本进行调整。为了更详细地介绍该框架，您可以参考另一篇关于从图形神经网络的角度关注​​PyNeuralogic的文章​​。

符号式Transformer​

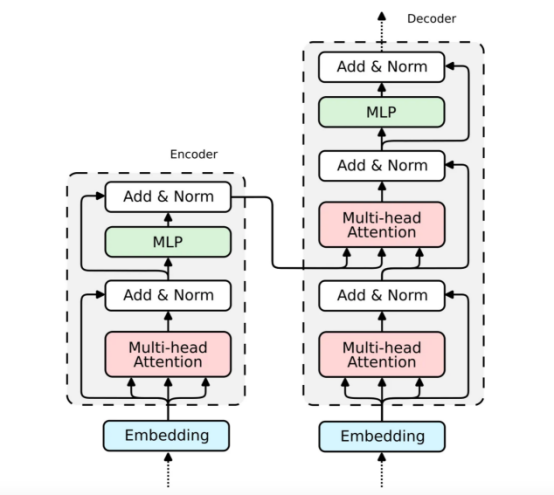
经典Transformer模型示意图​

Transformer架构由两个块组成——编码器（左）和解码器（右）。两个块共享相似之处——解码器是一个扩展编码器。因此，在本文中我们将只关注编码器的解析，因为解码器的实现是类似的。​

我们通常倾向于将深度学习模型实现为对批量输入到一个大张量中的输入令牌的张量操作。这是有意义的，因为深度学习框架和硬件（例如GPU）通常被优化为处理更大的张量，而不是不同形状和大小的多个张量。Transformers也不例外，通常将单个令牌向量表示批量化为一个大矩阵，并将模型表示为这些矩阵上的运算。然而，这样的实现隐藏了各个输入令牌之间的相互关系，正如Transformer的注意力机制所展示的那样。​

注意力机制​

注意力机制是所有Transformer模型的核心。具体来说，它的经典版本利用了所谓的多头缩放点积注意力。为了清晰起见，我们不妨借助于一个头来将缩放的点积注意力分解成一个简单的逻辑程序。​

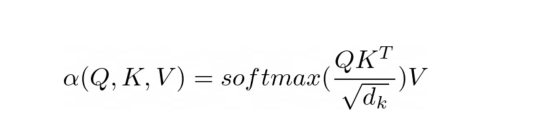
缩放的点积注意力方程​

注意力的目的是决定网络应该关注输入的哪些部分。注意力是通过计算值V的加权和来实现的，其中权重表示输入键K和查询Q的兼容性。在该特定版本中，通过查询Q和键K的点积的softmax函数除以输入特征向量维度d_k的平方根来计算权重。​

(R.weights(V.I, V.J) <= (R.d_k, R.k(V.J).T, R.q(V.I))) | [F.product, F.softmax_agg(agg_terms=[V.J])],​
(R.attention(V.I) <= (R.weights(V.I, V.J), R.v(V.J)) | [F.product]​

在PyNeuraLogic中，我们可以通过上述逻辑规则充分捕捉注意力机制。第一个规则表示权重的计算，它计算维度的平方根与转置的第j个关键向量和第i个查询向量的乘积。然后我们用softmax聚合给定i和所有可能j的所有结果。​

然后，第二条规则计算该权重向量与对应的第j个值向量之间的乘积，并对每个相应的第i个令牌的不同j的结果求和。​

注意力掩码​

在训练和评估期间，我们通常会限制输入令牌可以注意的内容。例如，我们希望限制令牌向前看并注意即将出现的单词。如PyTorch这样的流行框架是通过掩码技术实现这一点的，即通过将缩放的点积结果的元素子集设置为非常低的负数。这些数字强制softmax函数将零分配为相应令牌对的权重。​

(R.weights(V.I, V.J) <= (​
 R.d_k, R.k(V.J).T, R.q(V.I), R.special.leq(V.J, V.I)​
)) | [F.product, F.softmax_agg(agg_terms=[V.J])],​

通过我们的符号表示，我们可以通过简单地添加一个单体关系作为约束来实现这一点。在计算权重时，我们将j索引限制为小于或等于i索引。与掩码方案相反，我们只计算所需的缩放点积。​

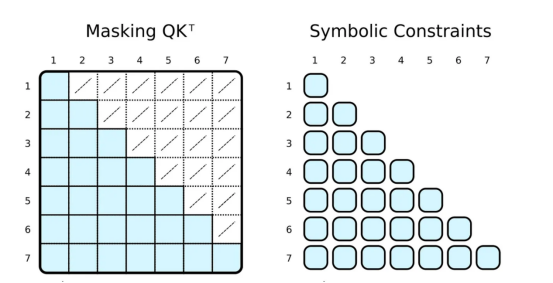
正则张量表示与符号表示中注意力的可视化​

常规的深度学习框架通过掩码（左侧）限制注意力。首先，计算整个QK^T矩阵，然后通过覆盖低值（白色交叉单元格）来屏蔽值，以模拟只注意相关的令牌（蓝色单元格）。在PyNeuraLogic中，我们通过应用符号约束（右侧）只计算所需的标量值，因此没有多余的计算。这一优势在以下注意力版本中更为显著。​

更优秀的注意力聚合​

当然，符号式的“掩码”可以是完全任意的。我们大多数人都听说过基于稀疏Transformer的GPT-3（或其应用程序，如ChatGPT，【引文4】）。稀疏Transformer的注意力（跨步版本）可分为两种类型的注意力头部：​

• 只关注前面的n个令牌（0≤i−j≤n）​
• 仅关注每n-th个前面的令牌（（i−j）%n=0）​

两种类型的头部的实现同样只需要微小的修改（例如，对于n＝5）。​

(R.weights(V.I, V.J) <= (​
 R.d_k, R.k(V.J).T, R.q(V.I),​
 R.special.leq(V.D, 5), R.special.sub(V.I, V.J, V.D),​
)) | [F.product, F.softmax_agg(agg_terms=[V.J])],​

(R.weights(V.I, V.J) <= (​
 R.d_k, R.k(V.J).T, R.q(V.I),​
 R.special.mod(V.D, 5, 0), R.special.sub(V.I, V.J, V.D),​
)) | [F.product, F.softmax_agg(agg_terms=[V.J])],​

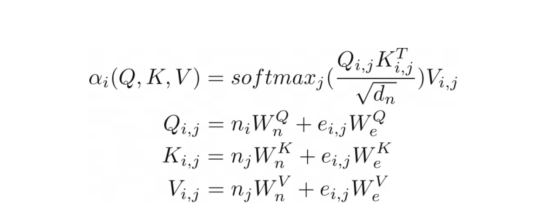
关系注意力方程​

其实，我们可以更进一步将注意力推广到类似于图的（关系）输入，就像在关系注意力中一样。这种类型的注意力作用于图，其中节点只关注其邻节点（由边连接的节点）。然后，查询Q、键K和值V是与节点向量嵌入相加的边缘嵌入。​

(R.weights(V.I, V.J) <= (R.d_k, R.k(V.I, V.J).T, R.q(V.I, V.J))) | [F.product, F.softmax_agg(agg_terms=[V.J])],​
(R.attention(V.I) <= (R.weights(V.I, V.J), R.v(V.I, V.J)) | [F.product],​

R.q(V.I, V.J) <= (R.n(V.I)[W_qn], R.e(V.I, V.J)[W_qe]),​
R.k(V.I, V.J) <= (R.n(V.J)[W_kn], R.e(V.I, V.J)[W_ke]),​
R.v(V.I, V.J) <= (R.n(V.J)[W_vn], R.e(V.I, V.J)[W_ve]),​

在我们的示例中，这种注意力与之前显示的缩放点积注意力几乎相同。唯一的区别是添加了额外的术语来捕捉边缘。将图形作为注意力机制的输入似乎很自然，考虑到Transformer是一种​​图形神经网络​​，作用于完全连接的图形（当不应用掩码时），这并不完全令人惊讶。在传统的张量表示中，这不是那么明显。

Transformer编码器​

现在，我们已经展示注意力机制的实现。其实，构建整个Transformer编码器块所缺少的部分也是比较直观的。​

嵌入​

我们已经在关系注意（Relational Attention）中看到了如何实现嵌入。对于传统的Transformer，嵌入都是非常相似的。我们只需将输入向量投影为三个嵌入向量——键、查询和值。​

R.q(V.I) <= R.input(V.I)[W_q],​
R.k(V.I) <= R.input(V.I)[W_k],​
R.v(V.I) <= R.input(V.I)[W_v],​

跳过连接、标准化和前馈网络​

查询嵌入通过跳过连接与注意力输出相加。然后将得到的向量归一化并传递到多层感知器（MLP）中。​

(R.norm1(V.I) <= (R.attention(V.I), R.q(V.I))) | [F.norm],​

对于MLP，我们将实现具有两个隐藏层的完全连接的神经网络，这可以优雅地表示为一个逻辑规则。​

(R.mlp(V.I)[W_2] <= (R.norm(V.I)[W_1])) | [F.relu],​

最后一个带有规范化的跳过连接与前一个相同。​

(R.norm2(V.I) <= (R.mlp(V.I), R.norm1(V.I))) | [F.norm],​

组装到一起​

至此，我们已经构建了Transformer编码器所需的所有部件。解码器使用相同的组件；因此，它的实现是类似的。现在，让我们将上面所有的代码块组合成一个可微的逻辑程序中。该程序可以嵌入到Python脚本内，并通过使用PyNeuraLogic被编译成神经网络。​

R.q(V.I) <= R.input(V.I)[W_q],​
R.k(V.I) <= R.input(V.I)[W_k],​
R.v(V.I) <= R.input(V.I)[W_v],​

R.d_k[1 / math.sqrt(embed_dim)],​
(R.weights(V.I, V.J) <= (R.d_k, R.k(V.J).T, R.q(V.I))) | [F.product, F.softmax_agg(agg_terms=[V.J])],​
(R.attention(V.I) <= (R.weights(V.I, V.J), R.v(V.J)) | [F.product],​

(R.norm1(V.I) <= (R.attention(V.I), R.q(V.I))) | [F.norm],​
(R.mlp(V.I)[W_2] <= (R.norm(V.I)[W_1])) | [F.relu],​
(R.norm2(V.I) <= (R.mlp(V.I), R.norm1(V.I))) | [F.norm],​

结论​

在本文中，我们分析了Transformer架构，并演示了它在一个称为​​PyNeuraLogic​​​的神经符号框架中的实现。通过这种方法，我们能够在只需对代码进行微小的更改的情况下实现各种类型的Transformer，从而向广大读者展示了如何快速地转向和开发新的Transformer架构。此外，文章还指出了各种版本的Transformer以及带有图形神经网络（GNN）的Transformer的明显相似之处。

参考文献​

[1]: Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A., Kaiser, L., & Polosukhin, I.. (2017). Attention Is All You Need.​

[2]: Marcus, G.. (2020). The Next Decade in AI: Four Steps Towards Robust Artificial Intelligence.​

[3]: Gustav Šourek, Filip Železný, & Ondřej Kuželka (2021). Beyond graph neural networks with lifted relational neural networks. Machine Learning, 110(7), 1695–1738.​

[4]: Brown, T., Mann, B., Ryder, N., Subbiah, M., Kaplan, J., Dhariwal, P., Neelakantan, A., Shyam, P., Sastry, G., Askell, A., Agarwal, S., Herbert-Voss, A., Krueger, G., Henighan, T., Child, R., Ramesh, A., Ziegler, D., Wu, J., Winter, C., Hesse, C., Chen, M., Sigler, E., Litwin, M., Gray, S., Chess, B., Clark, J., Berner, C., McCandlish, S., Radford, A., Sutskever, I., & Amodei, D.. (2020). Language Models are Few-Shot Learners.​

[5]: Child, R., Gray, S., Radford, A., & Sutskever, I.. (2019). Generating Long Sequences with Sparse Transformers.​

1. : Diao, C., & Loynd, R.. (2022). Relational Attention: Generalizing Transformers for Graph-Structured Tasks.​

译者介绍​

朱先忠，51CTO社区编辑，51CTO专家博客、讲师，潍坊一所高校计算机教师，自由编程界老兵一枚。​

原文标题：​​Beyond Transformers with PyNeuraLogic​​，作者：Lukáš Zahradník