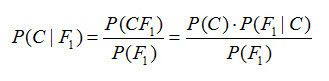CRPS：贝叶斯机器学习模型的评分函数-机器学习贝叶斯

连续分级概率评分（Continuous Ranked Probability Score, CRPS）或“连续概率排位分数”是一个函数或统计量，可以将分布预测与真实值进行比较。

机器学习工作流程的一个重要部分是模型评估。这个过程本身可以被认为是常识：将数据分成训练集和测试集，在训练集上训练模型，并使用评分函数评估其在测试集上的性能。

评分函数（或度量）是将真实值及其预测映射到一个单一且可比较的值 [1]。例如，对于连续预测可以使用 RMSE、MAE、MAPE 或 R 平方等评分函数。如果预测不是逐点估计，而是分布呢？

在贝叶斯机器学习中，预测通常不是逐点估计，而是值的分布。例如预测可以是分布的估计参数，或者在非参数情况下，来自MCMC方法的样本数组。

在这种情况下，传统的评分函数不适合统计设计;预测的分布聚合成它们的平均值或中值会导致关于预测分布的分散和形状的大量信息的损失。

CRPS

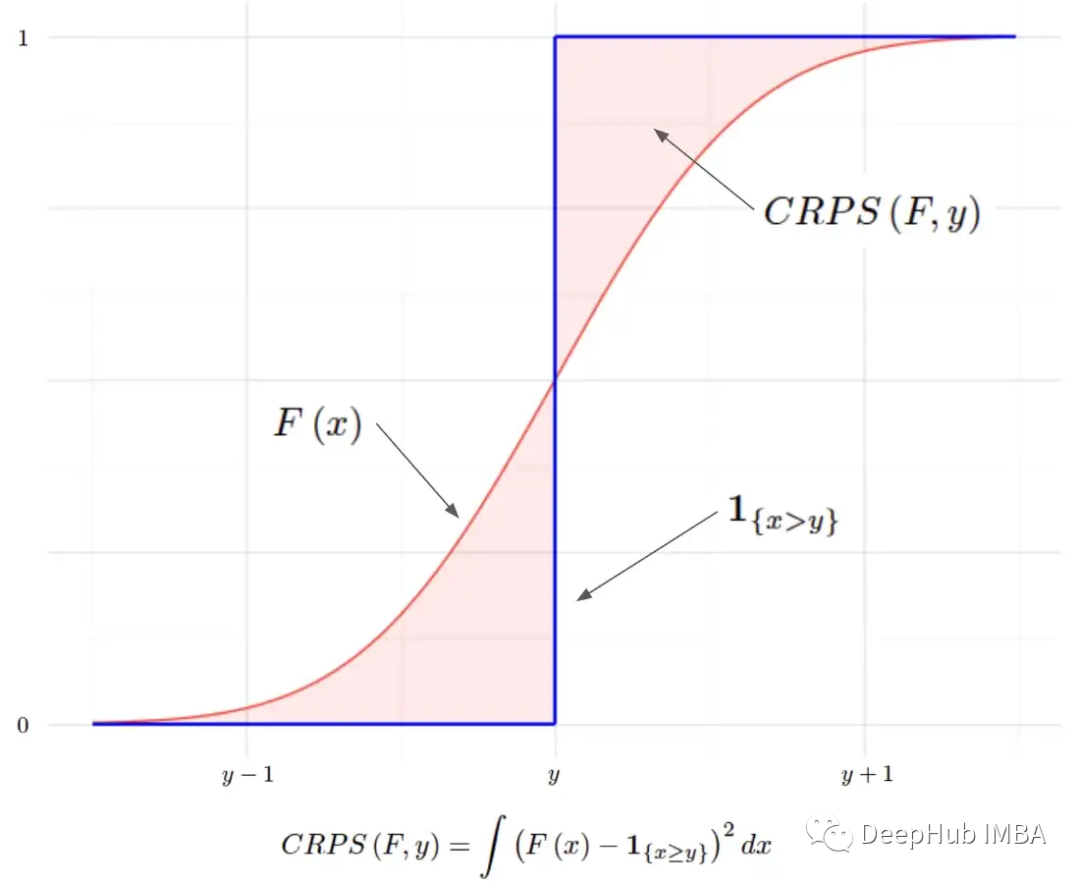
连续分级概率评分(CRPS)是一个分数函数，它将单个真实值与累积分布函数(CDF)进行比较:

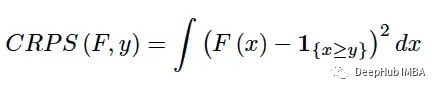
它于 70 年代首次引入 [4]，主要用于天气预报，现在在文献和行业中重新受到关注 [1] [6]。当目标变量是连续的并且模型预测目标的分布时，它可以用作评估模型性能的指标；示例包括贝叶斯回归或贝叶斯时间序列模型 [5]。

通过使用CDF， CRPS 对于参数和非参数预测都很有用：对于许多分布，CRPS [3] 都有一个解析表达式，对于非参数预测， CRPS 使用经验累积分布函数 (eCDF)。

在计算测试集中每个观察值的 CRPS 后，还需要将结果聚合成一个值。与 RMSE 和 MAE 类似，使用（可能是加权的）平均值对它们进行汇总：

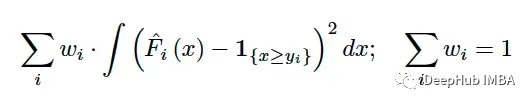
将单个值与分布进行比较的主要挑战是如何将单个值转换成为分布的表示。CRPS通过将基本真值转换为带有指标函数的退化分布来解决这一问题。例如如果真值是7，我们可以用:

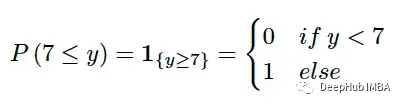
指标函数是一个有效的 CDF，可以满足 CDF 的所有要求。然后就可以将预测分布与真值的退化分布进行比较。我们肯定希望预测的分布尽可能接近真实情况；所以可以通过测量这两个 CDF 之间的（平方）面积来数学表示：

MAE与MAE关系

CRPS与著名的MAE(平均绝对误差)密切相关。如果采用逐点预测将其视为退化 CDF 并将其注入 CRPS 方程可以得到：

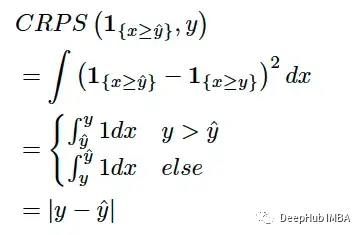
所以如果预测分布是退化分布（例如逐点估计），则 CRPS 会降低为 MAE。这有助于我们从另一个角度理解CRPS：它可以被视为将 MAE 推广到分布的预测中，或者说当预测分布退化时，MAE 是 CRPS 的特例。

当模型的预测是参数分布时（例如需要预测分布参数），CRPS 对一些常见的分布有一个解析表达式 [3]。如果模型预测正态分布的参数 μ 和 σ，则可以使用以下公式计算 CRPS：

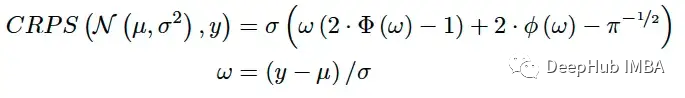
这个方案可以解决已知的分布，如Beta, Gamma, Logistic，对数正态分布和其他[3]。

当预测是非参数的，或者更具体地说——预测是一系列模拟时，计算 eCDF 是一项繁重的任务。但是CRPS 也可以表示为：

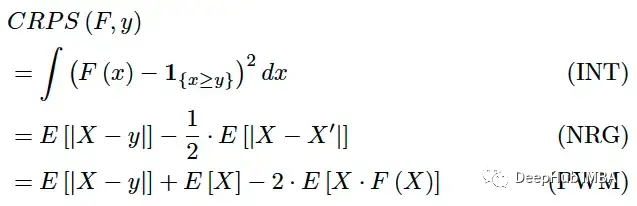
其中 X, X' 是 F 独立同分布。这些表达式虽然仍然需要一些计算量，但更易于计算。

Python实现

import numpy as np
 
 
 # Adapted to numpy from pyro.ops.stats.crps_empirical
 # Copyright (c) 2017-2019 Uber Technologies, Inc.
 # SPDX-License-Identifier: Apache-2.0
 def crps(y_true, y_pred, sample_weight=None):
     num_samples = y_pred.shape[0]
     absolute_error = np.mean(np.abs(y_pred - y_true), axis=0)
 
     if num_samples == 1:
         return np.average(absolute_error, weights=sample_weight)
 
     y_pred = np.sort(y_pred, axis=0)
     diff = y_pred[1:] - y_pred[:-1]
     weight = np.arange(1, num_samples) * np.arange(num_samples - 1, 0, -1)
     weight = np.expand_dims(weight, -1)
 
     per_obs_crps = absolute_error - np.sum(diff * weight, axis=0) / num_samples**2
     return np.average(per_obs_crps, weights=sample_weight)

根据NRG形式[2]实现的CRPS函数。改编自pyroppl[6]

import numpy as np
 
 
 def crps(y_true, y_pred, sample_weight=None):
     num_samples = y_pred.shape[0]
     absolute_error = np.mean(np.abs(y_pred - y_true), axis=0)
 
     if num_samples == 1:
         return np.average(absolute_error, weights=sample_weight)
 
     y_pred = np.sort(y_pred, axis=0)
     b0 = y_pred.mean(axis=0)
     b1_values = y_pred * np.arange(num_samples).reshape((num_samples, 1))
     b1 = b1_values.mean(axis=0) / num_samples
 
     per_obs_crps = absolute_error + b0 - 2 * b1
     return np.average(per_obs_crps, weights=sample_weight)

上面代码是根据PWM形式[2]实现CRPS。

总结

连续分级概率评分 (CRPS) 是一种评分函数，用于将单个真实值与其预测分布进行比较。此属性使其与贝叶斯机器学习相关，其中模型通常输出分布预测而不是逐点估计。它可以看作是众所周知的 MAE 对分布预测的推广。

它具有用于参数预测的解析表达式，并且可以针对非参数预测进行简单计算。CRPS 可能会成为评估具有连续目标的贝叶斯机器学习模型性能的新标准方法。