我们一起再聊聊B-Tree的Golang实现-51CTO.COM

这是B-Tree合集的第二部分。在这一部分会实现基本的数据结构和Search。

基本数据结构

根据Part1介绍的B-Tree的属性，我们可以建立node和tree两个基本的数据结构

type BTreeNode struct {
  keys []int        // An array of keys
  t    int          // Minimum degree
  c    []*BTreeNode // An array of child pointers
  n    int          // Current number of keys
  leaf bool         // Is true when node is leaf. Otherwise false
}

type BTree struct {
  root *BTreeNode // Pointer to root node
  t    int        // Minimum degree
}

// Constructor for BTreeNode
func NewBTreeNode(t int, leaf bool) *BTreeNode {
  return &BTreeNode{
    keys: make([]int, t<<1-1),
    t:    t,
    c:    make([]*BTreeNode, t<<1),
    leaf: leaf,
  }
}

// Constructor (Initializes tree as empty)
func NewBTree(t int) *BTree {
  return &BTree{
    t: t,
  }
}

Search

比如要在下面这个B树中找120

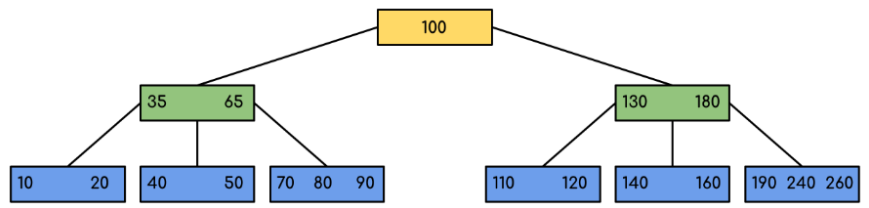
那么从Part1可知，我们都会从root出发，所以有下面3步即可找到120

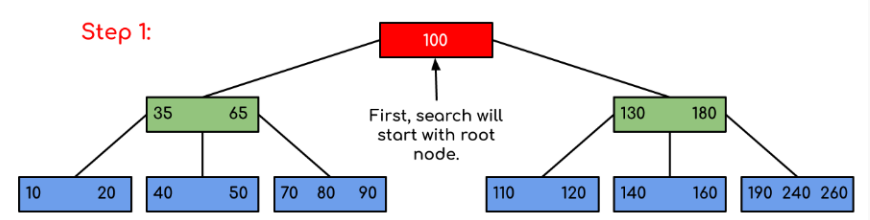
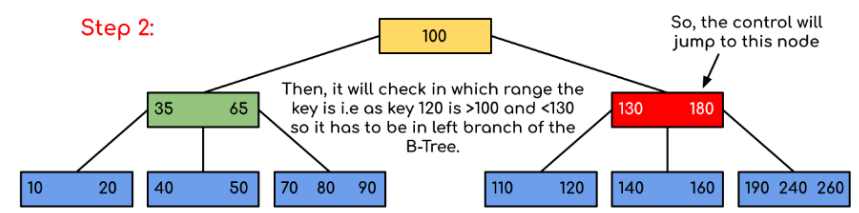
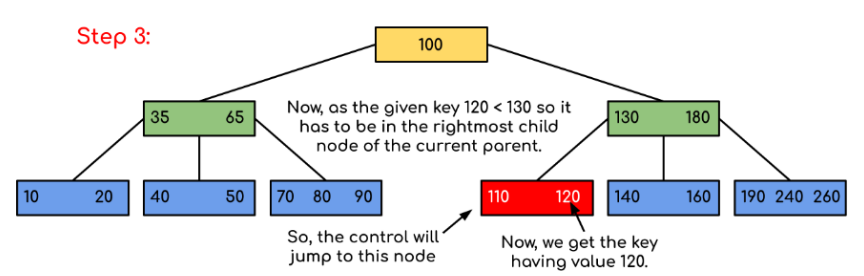
可见，可以用下面的伪代码来描述Search方法

对于红框里面的，意思是找第一个大于等于k的键index，但是伪代码用了顺序查找的方法，即O(N)。从Part1可知，node中的元素是从小到大排列的，所以我们可以用二分的方式优化。

// find the index of the first key which is greater or equal to k
func findGE(s []int, left, right, k int) int {
  if left <= right {
    mid := left + (right-left)>>1

    if k == s[mid] {
      return mid
    } else if k > s[mid] {
      return findGE(s, mid+1, right, k)
    } else {
      return findGE(s, left, mid-1, k)
    }
  }

  return left
}

下面是Search的代码

func (n *BTreeNode) search(k int) *BTreeNode {
  i := findGE(n.keys, 0, n.n-1, k)

  if n.keys[i] == k {
    return n
  }
  if n.leaf {
    return nil
  }
  return n.c[i].search(k)
}

func (t *BTree) Search(k int) *BTreeNode {
  if t.root != nil {
    return t.root.search(k)
  }

  return nil
}

在下次的Part3中，将实现B-Tree的Insert。