手写图表指南，你学会了吗？-51CTO.COM

1、前言

说到数据可视化，大家应该都不陌生。它旨在借助于图形化手段，清晰有效的传达与沟通信息。广义的数据可视化涉及信息技术、自然科学、统计分析、图形学等多种学科。

图例来源网络

我们熟知的图形、图表以及地图等都属于数据可视化的范畴。今天我们主要讨论数据可视化中的图表，像柱状图、折线图、面积图、饼图、热力图都是使用频率非常高的图表。

图例来源网络

如果要在移动端绘制一个类似于下图，使用真实数据渲染的简单面积图表，我们应该如何实现它呢？相信大家脑子里应该都有各种方案了，那么接下来我们就来一步步实现它。

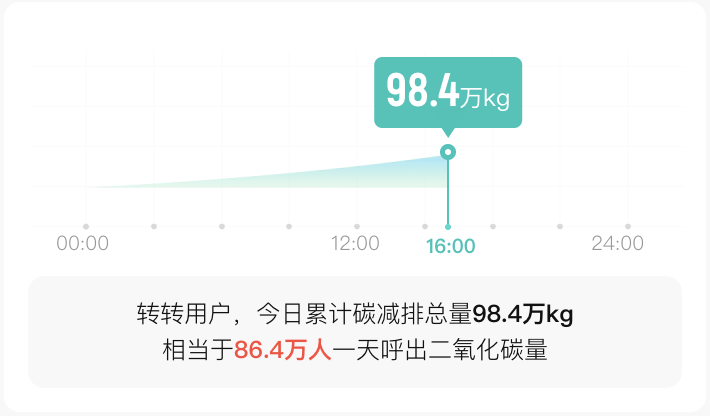
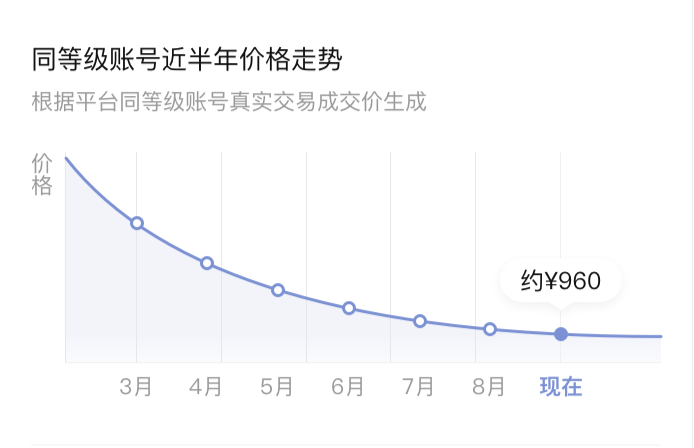
2、技术选型

需求

图表样式定制化图表样式为我司设计师独立设计，最终实现效果应该做到100%还原设计细节；
交互效果默认情况下数据游标只显示当前数据点，如需查看其他月份或者时刻数据，需要用户手动点击切换；
曲线面积图最终需要绘制出一个面积图，也就是用真实数据绘制出的曲线与坐标轴相交而形成的一个区域；

明确了具体的需求之后，我们就可以考虑技术方案选型了。

2.1 图表库

目前业界有很多成熟的图表库，像我们熟知的highcharts、echarts，Bizcharts，G2，更高阶的three.js等等。如果采用现有图表库来实现上述图表的话，会存在以下一些问题。

无法100%还原图表样式
包体积大，引入会造成项目性能问题

引入现有图表库的方案固然非常简单，大大节省了前端同学的开发量。但是存在着以上两个比较突出的问题。

图表库的图表样式都是通过配置完成，实现出来的效果在某些细节上难以完全还原设计稿，并且翻文档测试配置项的过程也比较繁琐。而且如果后续设计同学需要优化图表样式，并且此优化难以通过现有图表库配置项实现的话，那可能就需要二次开发图表库，对我们来说，也是一个不小的工作量；

通常C端的图表需求并不是那么通用，可能一个项目也就实现这么一两个图表，如果引入图表库的话，对项目本身来说，无形中又增加了一些打包成本。那有些同学可能会说，现在的某些图表库已经可以按需引用了，这样增加打包体积这个问题可能就不是问题了，虽然现在的某些比较成熟的图表库可以按需引用，但是在引用某个图表文件之前还是要引入一些核心文件，这些核心文件依然会占据不小的包体积。总结来说，引入现有图表库的方案成本高、灵活性差。

2.2 canvas

canvas相信对每一个前端开发者来说都不陌生，如果我们采用canvas来绘制图表的话，有两个问题比较棘手，上文中有提到过，我们要实现的图表是有交互效果的，当用户点击数据点的时候，则需要显示当前数据点的数据游标，再点击其他数据点的时候，数据游标也要相应的切换。大家都知道，使用原生canvas来实现事件系统异常麻烦，并且canvas的重绘机制也是我非常不喜欢的一点。总结一下，原生canvas没有完备的事件系统，重绘机制繁琐；

当然，现在也有很多优秀的canvas框架能够解决上述问题，比如fabric.js和konva.js，尤其是fabric.js，让我们使用canvas不再别扭，感兴趣的同学也可以尝试一下。

2.3 svg

svg是一种基于XML语法的图像格式，是可缩放的矢量图形。那什么是矢量图形呢？矢量图是计算机图形学中用点、直线或者多边形等基于数学方程的几何图元表示的图像，所以矢量图具有无论放大多少倍都不会失真的特性。而与之相对应的则是位图，位图是用像素阵列表示的图像。svg在绘制图表上有天然的优势，

开发成本低svg基于XML语法，XML语法是一种类似于HTML语法的可扩展标记语言，也就是说svg是使用一系列的元素(line、circle，polygon等)来描述图形的。那svg元素和dom元素之间是不是存在着某种关联呢？

我们由元素间的继承关系可以得出的结论是：svg元素和dom元素基本相似，因此对于svg元素，完全可以从dom元素的角度去理解和应用，上手成本几乎就可以忽略不计了。并且svg和css，javascript等其他网络标准无缝衔接。本质上，svg相对于图像，就好比html相对于文本；
完备的事件系统由于svg元素与dom元素类似，因此dom元素中的事件系统对于svg同样适用；
文件体积小，兼容性好前文已经介绍过，svg绘制出来的是一种矢量图形，而矢量图形都是使用点、直线等几何图元构成的图形，是对图像的图形描述，本质上依然是文本文件，所以它具有体积小的天然优势。svg是由万维网联盟（W3C）自1999年开始开发的开放标准。兼容性方面几乎所有主流浏览器都支持。

因此，最终我选择了使用svg来绘制图表。

3、svg基础

在我们正式绘制图表之前，首先需要了解一些svg的基础知识。

3.1 svg元素

svg图像就是使用不同的svg元素来创建的，svg元素常用的主要分为动画元素，形状元素，字体元素，图形元素，文本元素等。

形状元素<circle>, <ellipse>, <line>, <mesh>, <path>, <polygon>, <polyline>, <rect>形状元素是绘制svg图像最常用的，path元素是svg中一个非常强大的元素，它类似于canvas中的path，利用它能够绘制出任何你想要的图形。在我们本次绘制图表过程中，path元素亦不可或缺；
动画元素<animate>，<animateColor>，<animateMotion>，<animateTransform>，<discard>，<mpath>，<set>想要给svg元素添加动画，最简单的方式是使用动画元素，即用动画元素包裹住svg图形，即可添加动画；

其他元素就不再赘述。

3.2 svg应用场景

iconfont图标库和字体库iconfont图标库应该是svg最常见的一个使用场景，svg矢量图、文件小的特性使得它非常适合来绘制小图标，像我们转转的图标库也是使用svg来绘制的。svg绘制图标也有一些小小的缺点，比如它只能绘制纯色或者css渐变色图标，从颜色方面来说没有图片色系丰富，层次分明。
业务动画我们业务中一些常用的动画场景也会使用svg实现，比如loading效果，圆环进度条，商品添加购物车特效等；像商品添加购物车的特效在电商网站是非常常见的，一般我们的实现思路是使用js+css动画实现；其实svg中的路径动画更适用于这个场景，我们可以在需要加购的商品和购物车之间绘制一条隐形的path，当用户触发加购操作的时候触发路径动画，即animateMotion，这样也可以实现同样的功能。

4、svg如何绘制图表？

通过以上对背景以及一些前置知识的介绍，相信大家已经对svg有了一个初步的了解，接下来我们就回到最初的问题，如何通过svg来从头开始绘制一个曲线面积图？我主要分了以下几个步骤，下文会对每个步骤逐一进行说明。

4.1 坐标系

计算机绘图使用的坐标系统都是网格坐标系。其以左上角作为坐标系的原点，X轴正方形向右逐渐开始增大，Y轴正方向向下逐渐开始增大。

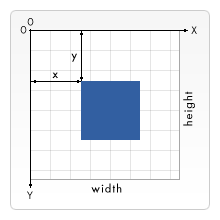
图例来源于网络

了解了svg的坐标系之后，我们来绘制曲线面积图中的坐标系，坐标系其实就是由两条线相交而成，svg中的line元素就是用来绘制直线的，所以使用line元素就可以绘制出X轴和Y轴。需要注意的是svg的坐标系原点在左上角，而我们需要实现的图表中坐标系原点在左下角，所以在实现的时候要对y轴的实际坐标进行处理。

createCoordinate() {
      this.svg.createLine(
        [
          {
            x1: '0',
            y1: '0',
            x2: '0',
            // ui设计稿上y轴高度为205，由于顶部游标的存在（游标高度57，宽度122），所以y轴变为205+57；
            // 由于整个坐标轴往下平移了57，所以最下面的坐标会出现不显示的情况，故再增加50的buffer
            y2: `${this.$toRealPx(262 + 50)}px`,
            stroke: '#F0F0F0',
            'stroke-width': '1',
          },
          {
            x1: '0',
            y1: `${this.$toRealPx(262 + 50)}px`,
            x2: `${this.$toRealPx(595)}px`,
            y2: `${this.$toRealPx(262 + 50)}px`,
            stroke: '#F0F0F0',
            'stroke-width': '1',
          },
        ],
        this.svgObj
      )
    }1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.

4.2 网格

在我们需要实现的两个图表中，图表背景处均有网格，网格的实现原理也是使用line元素，只要标记好起点以及终点，就可以完美绘制。此处不再展开。

4.3 数据点和数据游标

数据点：即用来标记当前数据位置的小原点，数据点有两种状态，分别是未点击态和点击态，实现数据点我们使用svg中的circle元素即可。当数据点被点击时，我们只需要更改circle元素的填充属性。

const circlePoints = this.graphAxisData.map((v, idx) => {
        return {
          cx: v.xAxis,
          cy: v.yAxis || 0,
          r: this.$toRealPx(5),
          stroke: '#7792D8',
          'stroke-width': this.$toRealPx(3),
          fill: 'white',
          title: `class${idx + 1}`,
          imageIndex: `imageClass${idx + 1}`,
        }
      })1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.

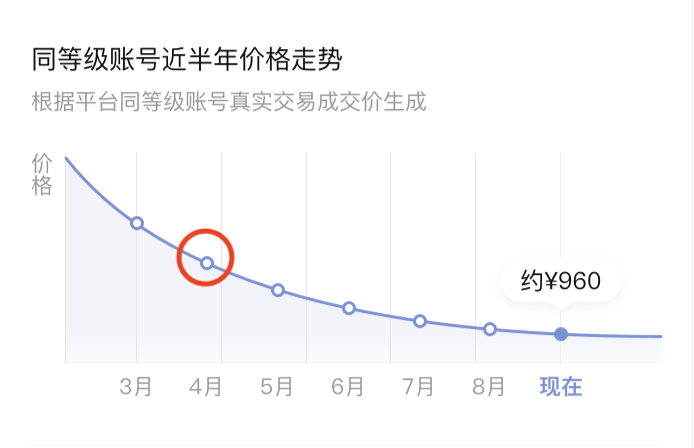
数据游标：数据游标在我们的图表里是一个不规则图形，其有点类似于会话气泡。我们要实现数据游标有两种方式，第一种方式是使用svg的path元素来绘制，那path元素的参数具体应该怎么设置呢？其实可以跟设计师同学沟通，一般设计同学在用设计软件导出的时候，设计软件会携带path元素的具体参数，这是方案一；还有第二种比较简单的方案是利用svg中的image元素，也就是将数据游标当作一个图片绘制到图表中，这种方案比较简单省事，我采用的也是此方案。

const circleImage = this.graphAxisData.map((v, idx) => {
        return {
          x: (v.xAxis - this.$toRealPx(122) / 2),
          y: (v.yAxis - this.$toRealPx(52) - this.$toRealPx(8)) || 0,
          height: this.$toRealPx(52),
          width: this.$toRealPx(122),
          id: `imageClass${idx + 1}`,
          href: 'https://pic3.zhuanstatic.com/zhuanzh/b13744dd-c240-4961-8054-9f923586ea5a.png',
        }
      })
      const circleText = this.graphAxisData.map((v, idx) => {
        return {
          x: v.xAxis,
          y: (v.yAxis - this.$toRealPx(52 / 2)) || 0,
          fill: '#111111',
          'font-size': this.$toRealPx(24),
          'text-anchor': 'middle',
          title: `¥${v.oriYAxis}`,
          id: `class${idx + 1}`,
        }
      })1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.

4.4 曲线

接下来就要绘制图表中最重要的一个部分，也就是用真实数据渲染出来的一条曲线，绘制曲线我们依然是利用path元素绘制贝塞尔曲线，贝塞尔曲线只需要少量的点就可以绘制一条光滑曲线。在svg中，path元素用来绘制贝塞尔曲线的命令有两组，第一组是C,S命令，用来绘制三次贝塞尔曲线；第二组是Q,T命令，用来绘制二次贝塞尔曲线。

我绘制图表使用的是三次贝塞尔曲线，那首先了解一下三次贝塞尔曲线。

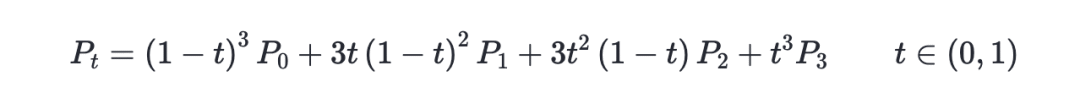
其中，t代表斜率，取值为0-1;p0代表起始点坐标(x0,y0);p1代表第一个控制点坐标(x1,y1);p2代表第二个控制点坐标(x2,y2);p3代表终点坐标(x3,y3);pt代表这条曲线上的任意一个点坐标(xt,yt)。当t由0-1逐渐变化的时候，可以得到一系列的(xt,yt),这一系列(xt,yt)就组成了一条三次贝塞尔曲线，这就是三次贝塞尔曲线的定义。

通过以上介绍可知，绘制三次贝塞尔曲线必须得知道起始点、两个控制点以及终点。后端会返回给我们相应的几个数据点，也就是说这几个数据点的坐标是已知的，现在的问题就成了给定一组已知数据点，如何拟合成一条曲线？其实思路很简单，假如说有已知的5个点，那么我们将第一个点作为起始点，第二个点作为终点，计算出他们之间的控制点，绘制一条曲线，同样的，又以第二个点作为起点，第三个点作为终点，再重复以上过程，最终即绘制出一条横穿五个点的平滑曲线。

此处附上算法源码

createBezierLine() {
      const polygonPath = this.getCubicBezierCurvePath(
        this.graphAxisData.map((v) => {
          return {
            x: v.xAxis,
            y: v.yAxis,
          }
        })
      )

      this.svg.createPath(
        {
          d: polygonPath,
          fill: 'none',
          stroke: '#7792D8',
          'stroke-width': 2
        },
        this.svgObject
      )
    }
    
getCubicBezierCurvePath(knots) {
      const firstControlPoints = []
      const secondControlPoints = []
      const path = []

      this.getCubicBezierCurvePoints(knots, firstControlPoints, secondControlPoints)

      for (let i = 0, len = knots.length; i < len; i++) {
        if (i === 0) {
          path.push(['M', knots[i].x, knots[i].y].join(' '))
        } else {
          const firstControlPoint = firstControlPoints[i - 1]
          const secondControlPoint = secondControlPoints[i - 1]
          path.push(
            [
              'C',
              firstControlPoint.x,
              firstControlPoint.y, // 第一个控制点
              secondControlPoint.x,
              secondControlPoint.y, // 第二个控制点
              knots[i].x,
              knots[i].y, // 实点
            ].join(' ')
          )
        }
      }

      return path.join(' ')
    }
    
getCubicBezierCurvePoints(knots, firstControlPoints, secondControlPoints) {
      const rhs = []
      const n = knots.length - 1
      let x = 0
      let y = 0
      let i = 0

      if (n < 1) {
        return
      }

      // Set right hand side X values0
      for (i = 0; i < n - 1; ++i) {
        rhs[i] = 4 * knots[i].x + 2 * knots[i + 1].x
      }
      rhs[0] = knots[0].x + 2 * knots[1].x
      rhs[n - 1] = 3 * knots[n - 1].x

      // Get first control points X-values
      x = this.getFirstControlPoints(rhs)

      // Set right hand side Y values
      for (i = 1; i < n - 1; ++i) {
        rhs[i] = 4 * knots[i].y + 2 * knots[i + 1].y
      }
      rhs[0] = knots[0].y + 2 * knots[1].y
      rhs[n - 1] = 3 * knots[n - 1].y

      // Get first control points Y-values
      y = this.getFirstControlPoints(rhs)

      for (i = 0; i < n; ++i) {
        // First control point
        firstControlPoints[i] = {
          x: x[i],
          y: y[i],
        }

        // Second control point
        if (i < n - 1) {
          secondControlPoints[i] = {
            x: 2 * knots[i + 1].x - x[i + 1],
            y: 2 * knots[i + 1].y - y[i + 1],
          }
        } else {
          secondControlPoints[i] = {
            x: (knots[n].x + x[n - 1]) / 2,
            y: (knots[n].y + y[n - 1]) / 2,
          }
        }
      }
    }
    
getFirstControlPoints(rhs) {
      const n = rhs.length
      const x = [] // Solution vector.
      const tmp = [] // Temp workspace.
      let b = 2.0
      let i = 0
      x[0] = rhs[0] / b

      for (i = 1; i < n; i++) {
        // Decomposition and forward substitution.
        tmp[i] = 1 / b
        b = (i < n - 1 ? 4.0 : 2.0) - tmp[i]
        x[i] = (rhs[i] - x[i - 1]) / b
      }

      for (i = 1; i < n; i++) {
        x[n - i - 1] -= tmp[n - i] * x[n - i] // Backsubstitution.
      }
      return x
    }1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
79.
80.
81.
82.
83.
84.
85.
86.
87.
88.
89.
90.
91.
92.
93.
94.
95.
96.
97.
98.
99.
100.
101.
102.
103.
104.
105.
106.
107.
108.
109.
110.
111.
112.
113.
114.
115.
116.
117.
118.
119.
120.
121.
122.
123.
124.

4.5 面积

最后一步就是绘制曲线与X轴和Y轴相交而形成的面积部分。假如说这条曲线不是一条曲线而是一条折线的话，那么其实很容易就能实现。我们将这条折线与X轴和Y轴连接起来形成一个闭合图形polygon，然后通过给polygon进行填充即可得到折线的面积图。

我们利用这个思路，如果一条折线上的点足够多的话，那么这条折线就会无限趋近于一条曲线。反之，一条曲线也可以看成是无限多的点构成的折线，所以我们利用svg中的getTotalLength()和getPointAtLength()这两个方法就可以将path转换为多边形，最后再填充多边形即可得到最终的面积图。

5、结语

通过以上5个步骤，我们就能够基于svg从头开始实现一个简单的曲线面积图。svg的使用场景还是非常丰富的，并且兼容性一直都不错，如果需要实现这种相对不那么复杂且交互少的图形，svg还是一个不错的方案。如果要实现复杂图层、复杂动效以及复杂交互，canvas框架可能会是一个更好的选择。

最后，开年第一篇，祝大家新年快乐，2023突（兔）飞猛进，大展鸿图（兔），前途（兔）无量！

参考

https://www.infoq.cn/article/ogwddr4u8x0s*5aaytsh https://gist.github.com/mingzhi22/be3324ffd9765687ea2f