单核M1 CPU上实现FP32 1.5 TFlops算力？这是一份代码指南-51CTO.COM

1.5 TFlops 到底有何魅力？

首先，这是在电池供电的单核 MacBook Air 2020 上运行；

其次，这会以每条指令约 0.5 纳秒的延迟运行。

那些强大的加速器或 GPU 张量核不在我们的考虑范畴。我们这里讨论的是与 CPU 寄存器相隔一个周期的实际线性代数性能。

奇怪的是，苹果一直在向我们隐瞒这一点。在本文中，我们将通过一些代码来揭开迷雾。

什么是 AMX 协处理器？

它可以说是 SIMD 的典范。一个重要的区别是 AMX:CPU 比率不是 1:1；并非每个内核都有自己的 AMX 协处理器。

以下是用于加载或存储值的规格：

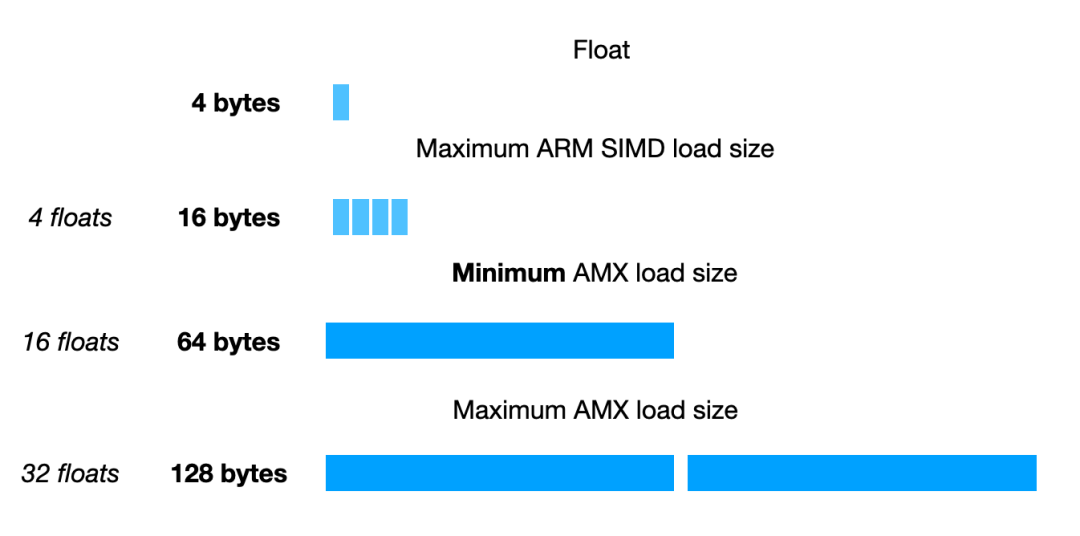
最小值与完整的 AVX512 寄存器一样宽

但这些值是从哪里加载或存储的？显然，这样的大小会很快用完整个 NEON 寄存器文件。不过 AMX 有一个单独的寄存器文件，这有些奇怪。

寄存器分为三组：X、Y 和 Z。对每个指令，X 和 Y 组保存输入，Z 组保存输出。

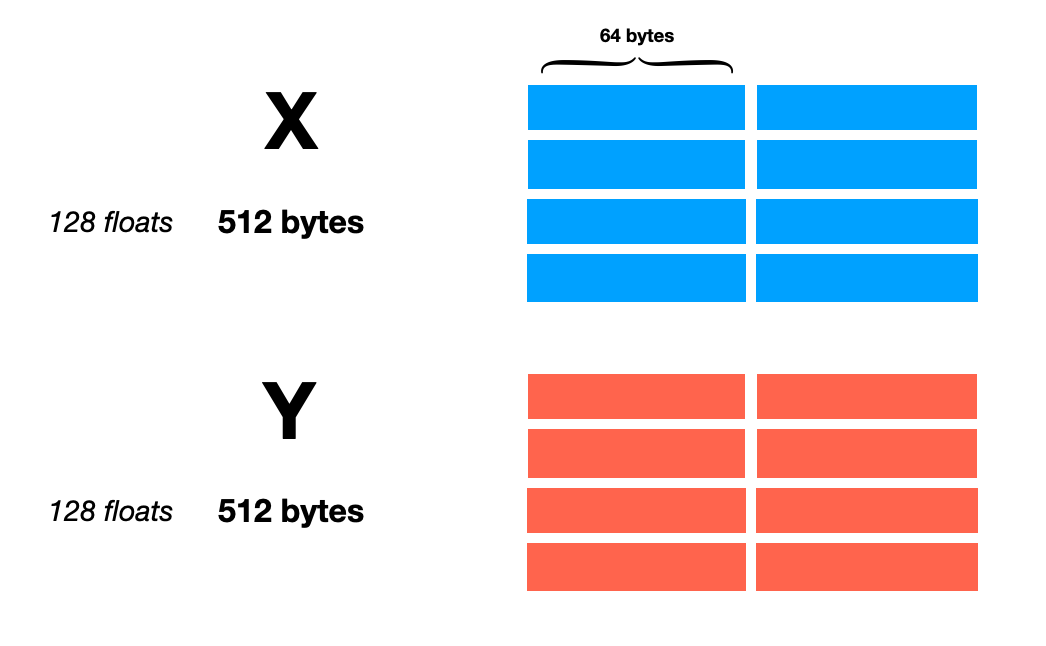
如我们所见，X 和 Y 相当大。二者之间有一个完整的 KB。Z 则令人称奇，然后是一些：

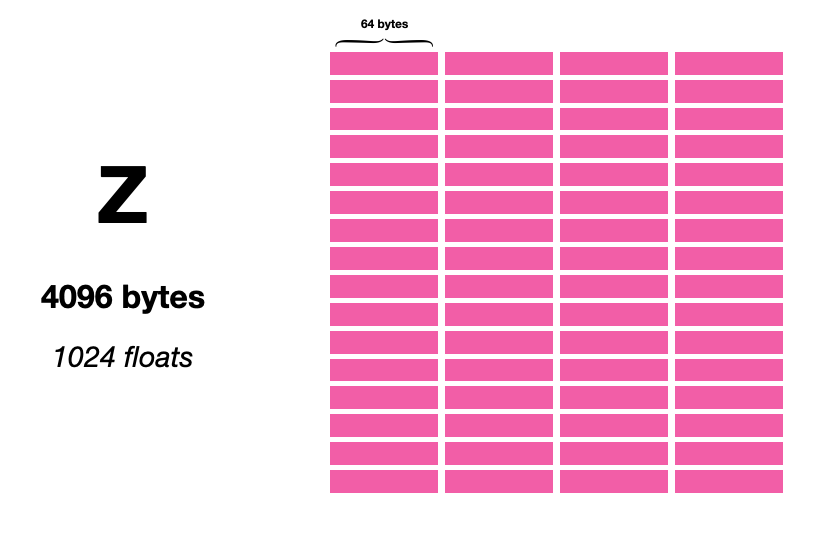
（剧透：一条 AMX 指令可以填充 1024 字节（Z 寄存器的 1/4）。）

那么如何从 X 和 Y 到 Z？方法很多，以至于它不那么适合 ISA 编码。所以苹果决定将大部分指令信息编码在通用寄存器中。事实证明，这个决定很赞，因为可以在 AMX 上执行代码的运行时（动态）配置。

这篇文章旨在提高协处理器利用效率。有一些 vector-vector 指令可以输出长度相同的向量，但不会使芯片的计算能力饱和。反而必须借助外积来进行。

何为外积？假设有两个输入向量 u 和 v：

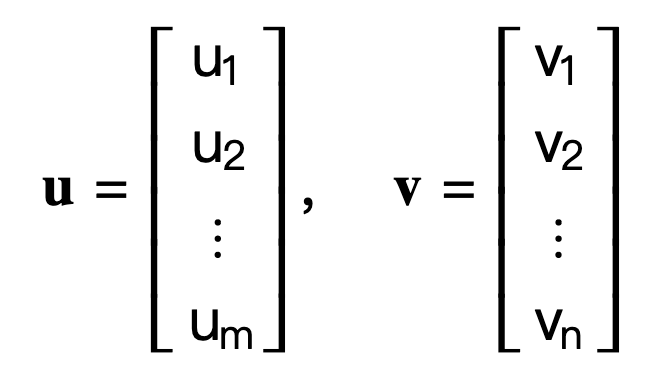
外积是一个矩阵，包含各元素可能组合对的乘积。（这里给出一些提示，说明为什么 Z 寄存器组比 X 和 Y 大得多。）

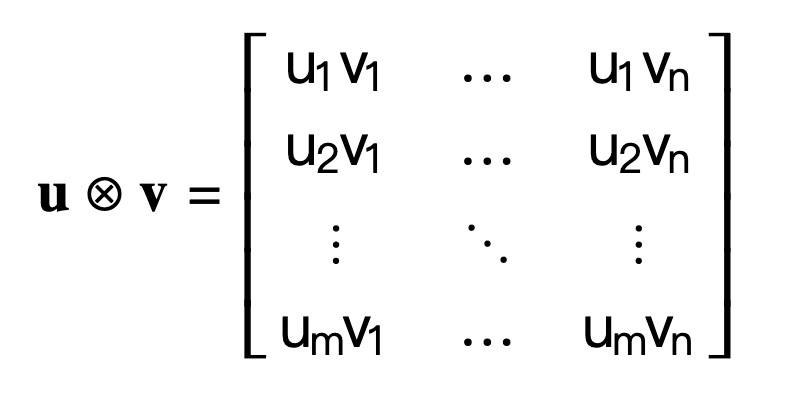
在 AMX 芯片上，可归结为一个非常简单的指令，就像这样：

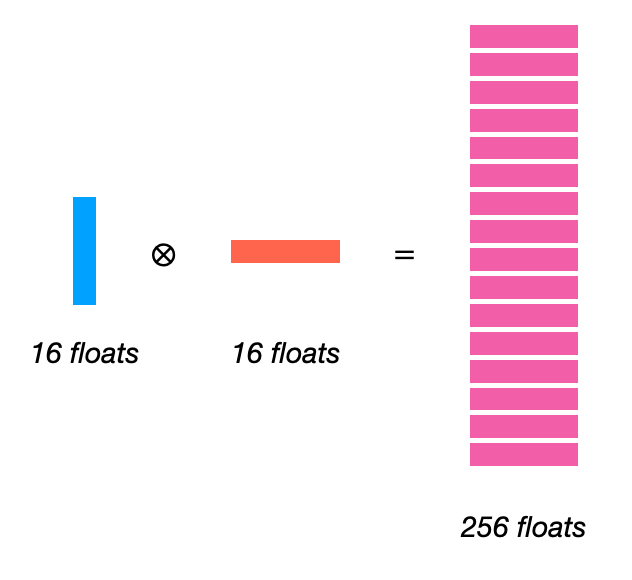
可以设置一个标志，使其从上一个结果中累加：

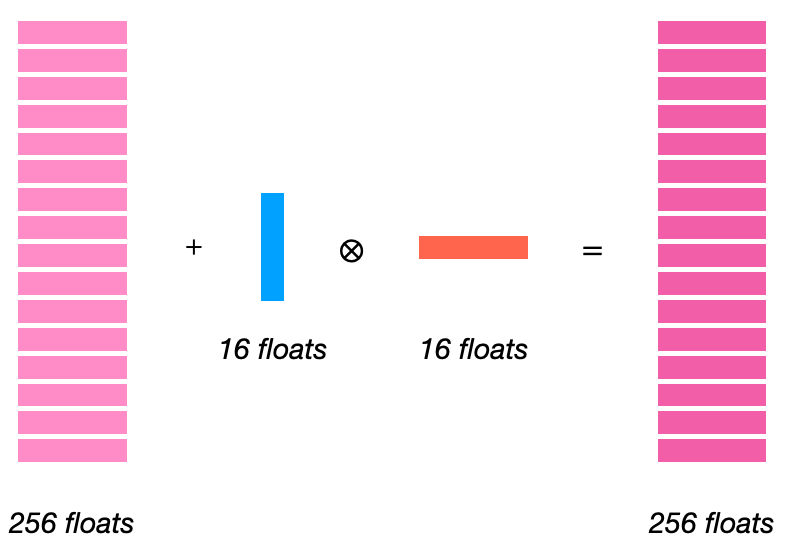
这样，我们就完全具备了编写矩阵乘法所需：从输入矩阵中重复加载 16 个浮点数，并将它们的外积累加成 16x16 输出。缩小 K 尺寸甚至无关紧要！

我们简化一下这个问题，并隐式转置矩阵乘法。A 和 B（输入）都将 K（缩减维度）作为主导维度。这在实践中并不重要，但它大大简化了我们的代码。

这里有一个参考，可用来检查我们提出的解决方案：

void reference_16x16xK (float *A, float *B, float *C, uint64_t K) {
  for (uint32_t m = 0; m < 16; ++m) {
    for (uint32_t n = 0; n < 16; ++n) {
      C [n * 16 + m] = 0;
      for (uint32_t k = 0; k < K; ++k) {
        C [n * 16 + m] += A [k * 16 + m] * B [k * 16 + n];
      }
    }
  }
}

下面是我们在 AMX 中的实现方法：

/only set for k == 0uint64_t reset_z = 1ull << 27;
for (uint32_t k = 0; k < K; ++k) {
  uint64_t idx = k % 4;
  // 64 bytes = 16 floats
  AMX_LDX ((uint64_t) A + k * 64);
  AMX_LDY ((uint64_t) B + k * 64);
  
  //now we do 4 indepedent outer products (avoiding pipeline hazards)
  AMX_FMA32 (reset_z);
  reset_z = 0;
}

神奇的是，我们没有处理任何寄存器，但却悄悄做了些处理。以同样的方式将 reset_z 编码为位掩码，寄存器地址也编码在传递给 AMX_* 的参数中。指向 A 和 B 的指针最多只能使用 56 位，因此苹果工程师将信息存储在其他 8 位中。我们只是意外将其全部设置为 0。因此，在本例中，对 X 和 Y 我们将寄存器置 “0”。

将 Z 寄存器存储到内存的代码有点复杂，因为我们只填充了第一列。所以需要获取寄存器 0、4、8 等：

for (uint64_t i = 0; i < 16; ++i) {
  const uint64_t z_register = (i * 4ull) << 56;
  AMX_STZ (z_register | (uint64_t) C + i * 64);
}

但你会发现，运行上面的代码非常慢。只有区区几百 GFlops。

为什么会这样？有两个原因。

开始的减速是流水线冒险。每个 AMX_FMA32 都依赖于前一个，因为全都累积到寄存器文件的一个子集中。我们最终只达到了寄存器文件全节流的 25%，剩余部分闲置，未能实现指令级并行。

接下来的问题是从内存中加载的效率很低。我们其实可以一次加载 128 个字节，但上面的代码只能加载 64 个字节。类似地，可以加载到其他寄存器，不必每次都加载到相同的寄存器。也可以实现一定程度的指令级并行。

那么计划是什么？

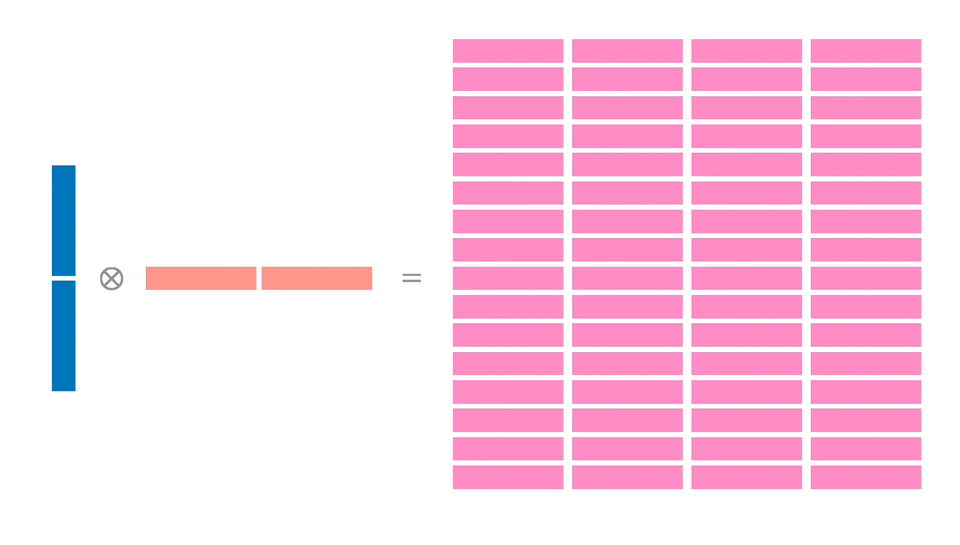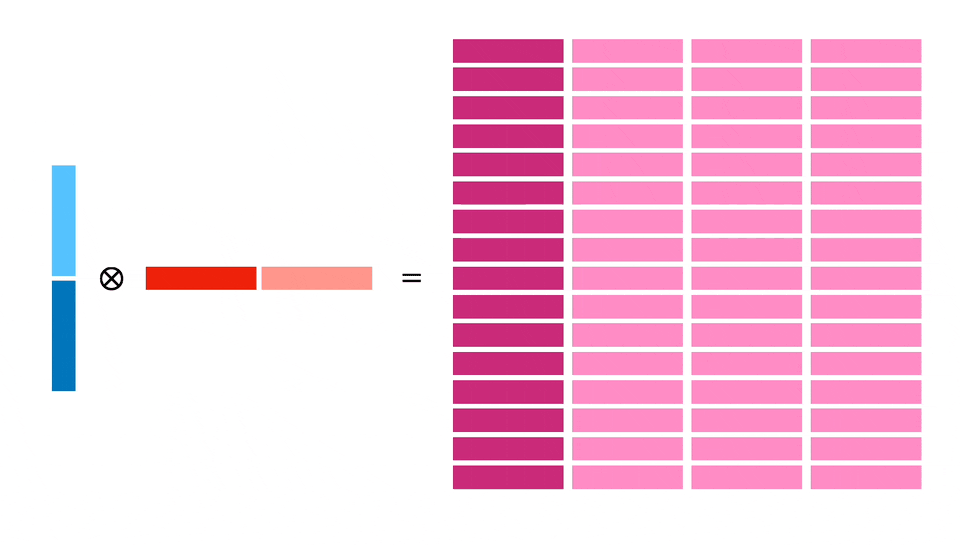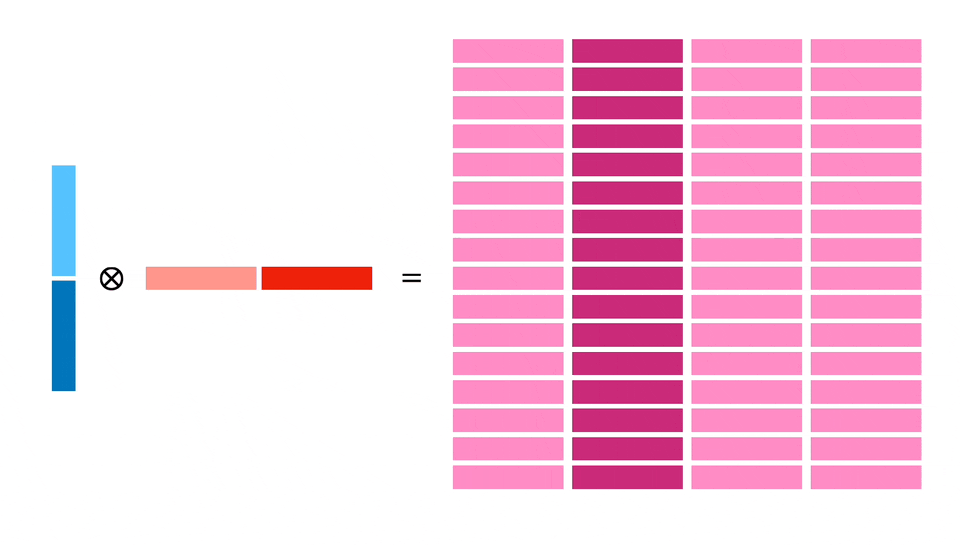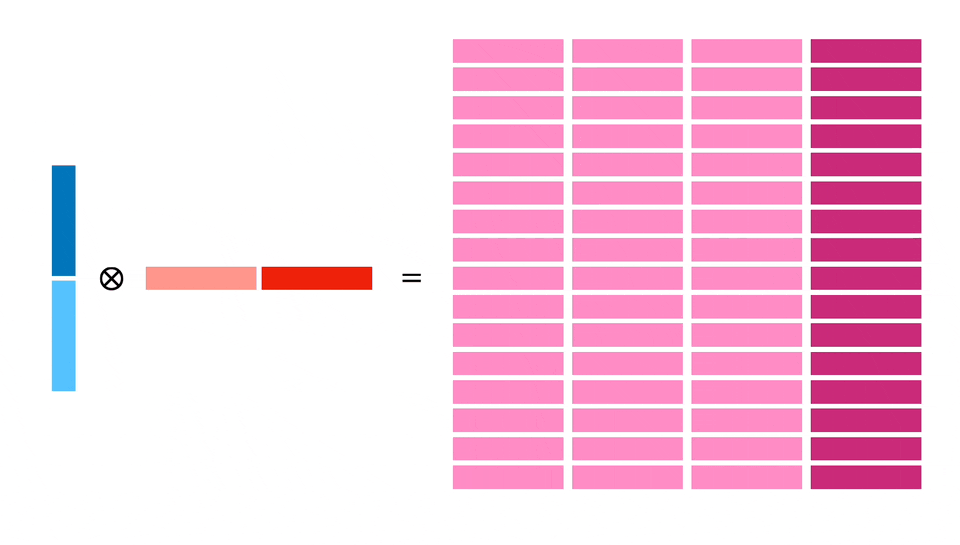
我们将向 X 和 Y 加载 128 个字节，然后计算一个 32x32 块。这将涉及 16x16 块的 4 次独立计算，形成指令级并行，可以更高效利用加载的内存（每个 64 字节寄存器使用两次）。

void mm32x32xK (float* A, float* B, float* C, uint64_t K) {

  //flag to load/store 128 bytes
  const uint64_t load_store_2 = 1ull << 62;
  const uint64_t load_store_width = 128; //in bytes

  //only set for k == 0
  uint64_t reset_z = 1ull << 27;


  for (uint32_t k = 0; k < K; ++k) {
    uint64_t idx = k % 4;
    //load to X, Y (skipping every other index because we're loading 128 bytes)
    AMX_LDX (load_store_2 | (idx * 2) << 56 | (uint64_t) A + k * load_store_width);
    AMX_LDY (load_store_2 | (idx * 2) << 56 | (uint64_t) B + k * load_store_width);

    //offset into X and Y registers is byte-wise
    const uint64_t offset = idx * load_store_width;

    //now we do 4 indepedent outer products (avoiding pipeline hazards)
    AMX_FMA32 (reset_z | (0ull << 20) | ((offset +  0ull) << 10) | ((offset +  0ull) << 0));
    AMX_FMA32 (reset_z | (1ull << 20) | ((offset + 64ull) << 10) | ((offset +  0ull) << 0));
    AMX_FMA32 (reset_z | (2ull << 20) | ((offset +  0ull) << 10) | ((offset + 64ull) << 0));
    AMX_FMA32 (reset_z | (3ull << 20) | ((offset + 64ull) << 10) | ((offset + 64ull) << 0));
    reset_z = 0;
  }

  for (uint64_t i = 0; i < 16; ++i) {
    //store interleaved
    AMX_STZ (load_store_2 | ((i * 4ull + 0) << 56) | (uint64_t) C + i * load_store_width);
    AMX_STZ (load_store_2 | ((i * 4ull + 2) << 56) | (uint64_t) C + (16 + i) * load_store_width);
  }
}

void mm32x32xK (float* A, float* B, float* C, uint64_t K){
  //flag to load/store 128 bytes  const uint64_t load_store_2 = 1ull << 62;  const uint64_t load_store_width = 128; //in bytes
  //only set for k == 0  uint64_t reset_z = 1ull << 27;

  for (uint32_t k = 0; k < K; ++k) {    uint64_t idx = k % 4;    //load to X, Y (skipping every other index because we're loading 128 bytes)    AMX_LDX (load_store_2 | (idx * 2) << 56 | (uint64_t) A + k * load_store_width);    AMX_LDY (load_store_2 | (idx * 2) << 56 | (uint64_t) B + k * load_store_width);
    //offset into X and Y registers is byte-wise    const uint64_t offset = idx * load_store_width;
    //now we do 4 indepedent outer products (avoiding pipeline hazards)    AMX_FMA32 (reset_z | (0ull << 20) | ((offset +  0ull) << 10) | ((offset +  0ull) << 0));    AMX_FMA32 (reset_z | (1ull << 20) | ((offset + 64ull) << 10) | ((offset +  0ull) << 0));    AMX_FMA32 (reset_z | (2ull << 20) | ((offset +  0ull) << 10) | ((offset + 64ull) << 0));    AMX_FMA32 (reset_z | (3ull << 20) | ((offset + 64ull) << 10) | ((offset + 64ull) << 0));    reset_z = 0;  }
  for (uint64_t i = 0; i < 16; ++i) {    //store interleaved    AMX_STZ (load_store_2 | ((i * 4ull + 0) << 56) | (uint64_t) C + i * load_store_width);    AMX_STZ (load_store_2 | ((i * 4ull + 2) << 56) | (uint64_t) C + (16 + i) * load_store_width);  }}

我在上面添加了注释，关于说明性标志有些有趣的细节。Corsix 在解释这一点上做得很好，所以我要留下链接：

加载和存储标志：https://github.com/corsix/amx/blob/main/ldst.md
FMA 标志：https://github.com/corsix/amx/blob/main/fma.md

那么我们到底能有多快？这一定程度上取决于 K，但我们达到了 1.5TFlops 处理的问题更大相对来说会获得更好的性能，这也不足为奇，因为缓存可以更好地预热，CPU 有更多时间交错指令。

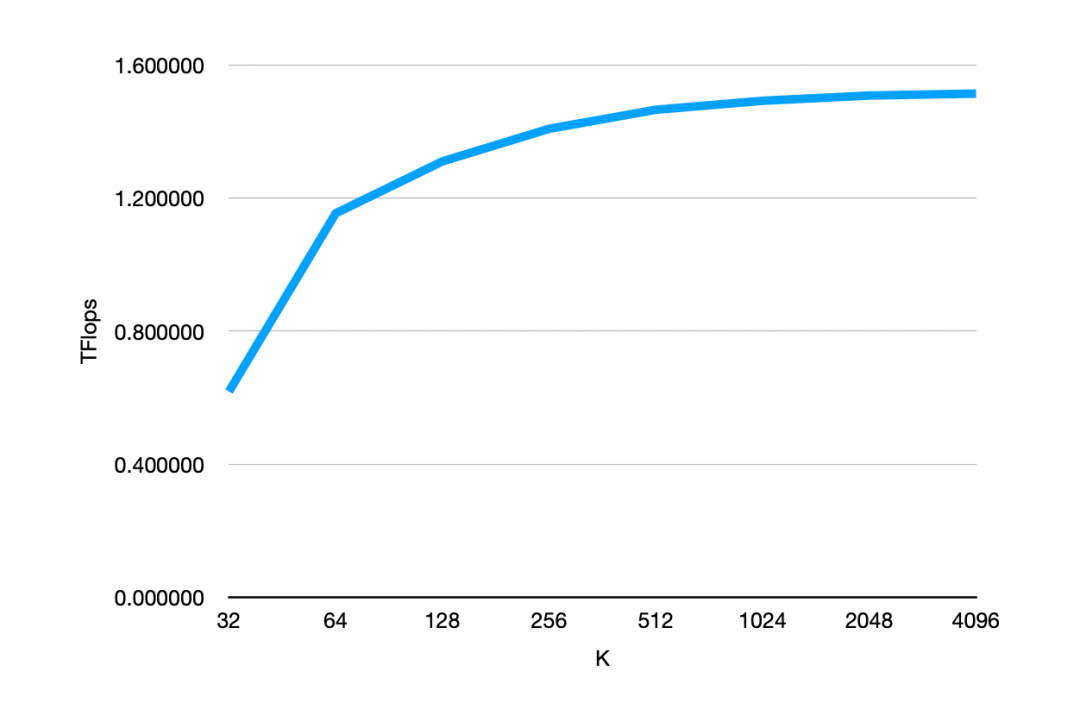
总的来说，在当今大型神经网络竞相追逐通用 AI 的背景下，这类问题显得微不足道，然而却为小型神经网络在现实计算中找到一席之地。如果一个预测模型可于几十纳秒内在电池供电的笔记本上运行，或将为原本可能使用探试算法的地方带来更多价值。你怎么看？

原文链接：https://jott.live/markdown/1.5tflop_m1