Part 01
● 什么是图嵌入 ●
图嵌入是将图结构数据映射为低维稠密向量的过程,同时使得原图中拓扑结构相似或属性接近的节点在向量空间上的位置也接近,能够很好地解决图结构数据难以高效输入机器学习算法的问题。
对于图的表示和存储,最容易想到的是使用邻接矩阵的方式。对图中的每个节点进行编号,构造出一个 的矩阵,其中
的矩阵,其中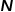 表示图中节点的数量。图中任意两个节点是否有边相连决定了邻接矩阵中对应位置的值,这种表示方法非常容易理解且直观,但是非常低效。因为现实场景中的图可能会包含成千上万甚至更多的节点,而大多数节点之间是没有边连接的,这会导致得到的邻接矩阵十分稀疏。使用邻接矩阵表示和存储图需要较高的计算成本和空间成本,而图嵌入算法能够高效解决图分析问题。
表示图中节点的数量。图中任意两个节点是否有边相连决定了邻接矩阵中对应位置的值,这种表示方法非常容易理解且直观,但是非常低效。因为现实场景中的图可能会包含成千上万甚至更多的节点,而大多数节点之间是没有边连接的,这会导致得到的邻接矩阵十分稀疏。使用邻接矩阵表示和存储图需要较高的计算成本和空间成本,而图嵌入算法能够高效解决图分析问题。
Part 02
● 基本概念 ●
概念1 图:
图表示为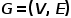 ,其中
,其中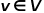 表示节点,
表示节点,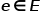 表示边。
表示边。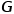 与节点类型映射函数
与节点类型映射函数 和边类型映射函数
和边类型映射函数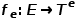 相关联。
相关联。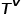 表示节点类型的集合,
表示节点类型的集合,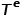 表示边类型的集合。
表示边类型的集合。
概念2 同构图:
图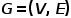 ,其中
,其中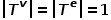 。也就是说,所有节点都属于一种类型,所有边都属于一种类型,比如社交网络中的用户关注关系图,只有用户这一种节点类型和关注关系这一种边类型。
。也就是说,所有节点都属于一种类型,所有边都属于一种类型,比如社交网络中的用户关注关系图,只有用户这一种节点类型和关注关系这一种边类型。
概念3 异构图:
图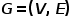 ,其中
,其中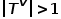 或
或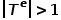 。也就是说,节点类型或边类型多于一种,比如学术网络中的图结构,存在论文、作者、会议等多种节点类型,边的关系包括作者与论文之间的创作关系、论文与会议之间的发表关系、论文与论文之间的引用关系等。
。也就是说,节点类型或边类型多于一种,比如学术网络中的图结构,存在论文、作者、会议等多种节点类型,边的关系包括作者与论文之间的创作关系、论文与会议之间的发表关系、论文与论文之间的引用关系等。
概念4 一阶相似度:
如果连接两个节点的边的权重较大,则它们之间的一阶相似度越大。节点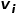 和节点
和节点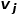 之间的一阶相似度表示为
之间的一阶相似度表示为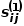 ,有
,有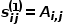 ,其中
,其中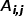 是节点
是节点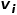 和节点
和节点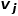 之间连边
之间连边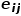 的权重。
的权重。
概念5 二阶相似度:
如果两个节点邻近的网络结构越相似,则它们之间的二阶相似度越大。节点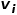 和节点
和节点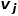 之间的二阶相似度
之间的二阶相似度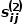 是
是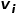 的邻域
的邻域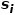 和
和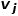 的邻域
的邻域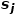 之间的相似性。如图1所示,因为有边连接节点f和节点g,所以节点f和节点g一阶相似。虽然没有边连接节点e和节点g,但是它们相同的邻居节点有四个,所以节点e和节点g二阶相似。
之间的相似性。如图1所示,因为有边连接节点f和节点g,所以节点f和节点g一阶相似。虽然没有边连接节点e和节点g,但是它们相同的邻居节点有四个,所以节点e和节点g二阶相似。
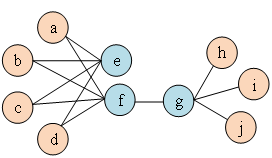
图1 二阶相似度示意图
概念6 图嵌入:
给定输入图,以及预定义的嵌入维数,图嵌入是要在尽可能保留图属性的前提下,将图转换到维空间。依赖一阶相似度或高阶相似度量化图属性的保留程度,使用一个维向量或一组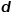 维向量来表示一个图,每个向量表示图的一部分的嵌入,例如节点或边。
维向量来表示一个图,每个向量表示图的一部分的嵌入,例如节点或边。
Part 03
● 图嵌入算法分类 ●
在过去几十年,研究人员们提出了许多优秀的算法,在社交网络、通信网络等场景中被证明具有显著的效果。业界通常根据输出粒度的差异将这些图嵌入算法分为以下三类:
(1)节点嵌入
节点嵌入是最常见的类型,在低维空间中用向量对图中的每一个节点进行表示,“相似”节点的嵌入向量表示也是相似的。当需要对图中的节点进行分析,进而执行节点分类或节点聚类等任务时,通常会选择节点嵌入。
(2)边嵌入
在低维空间中用向量对图中的每一条边进行表示。边由一对节点组成,通常表示节点对关系。当需要对图中的边进行分析,执行知识图谱关系预测或链路预测等任务时,适合选择边嵌入。
(3)图嵌入
在低维空间中用向量对整个图进行表示,通常是分子或蛋白质这样的小图。将图表示为一个向量便于计算不同图之间的相似性,从而解决图分类问题。
不同的任务需求决定了选用的图嵌入算法,由于篇幅原因,这里节选出节点嵌入中的DeepWalk算法和Node2Vec算法来进行相对详细的学习。
Part 04
● 经典图嵌入算法 ●
1.DeepWalk算法
受自然语言处理领域中word2vec思想的启发,Perozzi等为了建立学习图中节点表示向量的模型,将节点与节点的共现关系类比于语料库中词与词的共现关系,提出了DeepWalk算法。通过随机游走的方式采集图中节点的邻居节点序列,相当于节点上下文的语料库,进而可以解决图中节点之间共现关系的提取问题。预先设置好节点序列的长度和起点,随机游走策略将会指导如何在邻居节点中确定下一个游走节点,重复执行该步骤,即可获得满足条件的序列,随机游走示意图如图2所示。
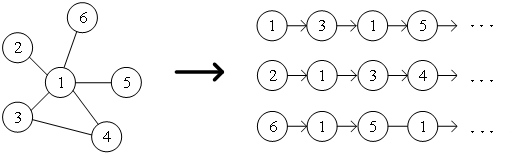
图2 随机游走示意图
将word2vec算法中的单词对应成图中的节点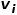 ,单词序列对应成随机游走得到的节点序列,那么对于一个随机游走
,单词序列对应成随机游走得到的节点序列,那么对于一个随机游走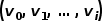 ,定义其优化目标函数如公式所示。
,定义其优化目标函数如公式所示。
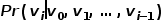
为了更进一步学习节点的潜在特征表示,DeepWalk算法引入了映射函数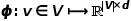 ,实现图中节点到
,实现图中节点到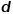 维向量的映射,那么问题就转换成要估算下列公式的可能性。
维向量的映射,那么问题就转换成要估算下列公式的可能性。
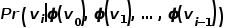
概率的计算同样需要参考word2vec算法中的skip-gram模型。
如图3所示,skip-gram模型包含两个关键的矩阵,一个是中心词向量矩阵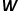 ,另一个是背景词向量矩阵
,另一个是背景词向量矩阵 ,这两个权重矩阵分别代表着作为不同角色时单词所关联的词向量。skip-gram是一个预测词上下文的模型,先从语料库中学习了词与词之间的关系,再用这些关系来表达一个特定词的上下文,即词的向量表示。也就是说,在同一个序列中,两个单词同时出现的频率越高,两个单词的向量表示越相似。将这个思想应用到图中,定义其优化目标函数如公式所示。
,这两个权重矩阵分别代表着作为不同角色时单词所关联的词向量。skip-gram是一个预测词上下文的模型,先从语料库中学习了词与词之间的关系,再用这些关系来表达一个特定词的上下文,即词的向量表示。也就是说,在同一个序列中,两个单词同时出现的频率越高,两个单词的向量表示越相似。将这个思想应用到图中,定义其优化目标函数如公式所示。
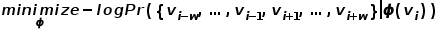
在随机游走过程中,不考虑采样序列中节点与节点的顺序关系,这能够更好地反映节点的邻近关系,同时减少了计算成本。
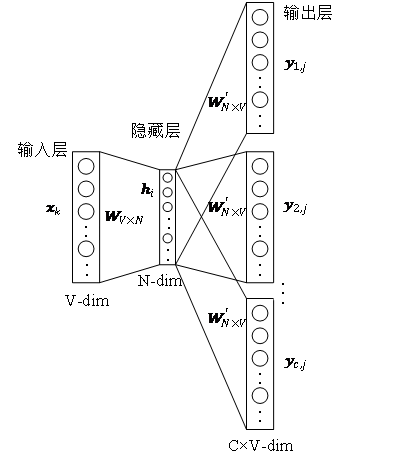
图3 skip-gram模型示意图
2.Node2Vec算法
在DeepWalk算法的基础上,研究者Grover A和Leskovec J提出了Node2Vec算法。Node2Vec算法对DeepWalk算法中通过随机游走生成节点序列的过程进行优化,定义参数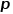 和参数
和参数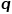 对每次随机游走是倾向于广度优先采样还是深度优先采样进行引导,因此适应性很高。假定当前访问节点
对每次随机游走是倾向于广度优先采样还是深度优先采样进行引导,因此适应性很高。假定当前访问节点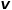 ,则下一个访问节点
,则下一个访问节点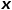 的概率如公式所示。
的概率如公式所示。
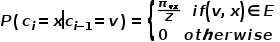
式中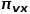 表示从节点
表示从节点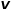 到节点
到节点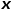 的转移概率,
的转移概率,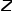 表示归一化常数。
表示归一化常数。
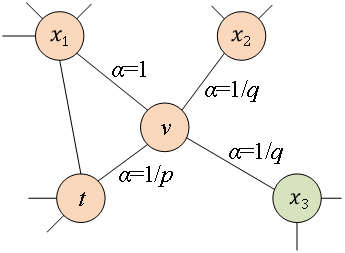
图4 Node2Vec随机游走策略示意图
Node2Vec的随机游走策略是根据两个参数进行控制的,如图4所示。假设经过边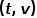 到达节点v,下一步准备访问节点x,设
到达节点v,下一步准备访问节点x,设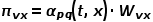 ,
,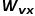 是节点
是节点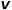 和
和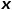 之间的边权。也就是说,当图是无权图时,
之间的边权。也就是说,当图是无权图时,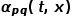 直接决定了节点的转移概率。当图是有权图时,
直接决定了节点的转移概率。当图是有权图时,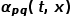 与边权重的乘积
与边权重的乘积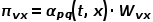 决定了节点最终的转移概率。
决定了节点最终的转移概率。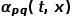 可以根据以下公式来计算,式中
可以根据以下公式来计算,式中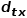 是节点
是节点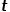 和节点
和节点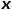 之间的最短路径距离。
之间的最短路径距离。
当游走采样从节点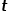 走到节点
走到节点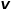 并需要选择下一跳节点时,会有以下三种情况。
并需要选择下一跳节点时,会有以下三种情况。
(1) 当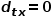 时,返回节点
时,返回节点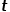 。
。
(2) 当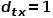 时,选择节点
时,选择节点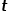 和节点
和节点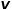 的共同邻接节点,例如节点
的共同邻接节点,例如节点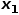 。
。
(3) 当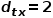 时,选择与节点
时,选择与节点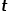 无关的节点
无关的节点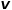 的邻接节点,例如节点
的邻接节点,例如节点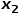 或
或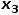 。
。
也就是说,参数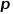 控制着返回上一跳节点的概率,参数
控制着返回上一跳节点的概率,参数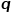 更多地控制的是探索网络的局部结构信息还是全局结构信息,DeepWalk模型其实是
更多地控制的是探索网络的局部结构信息还是全局结构信息,DeepWalk模型其实是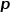 和
和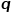 的值设置为1时的Node2Vec模型。
的值设置为1时的Node2Vec模型。
Part 05
● 总结 ●
随着信息技术的快速发展,网络环境变得日益复杂,网络攻击频发,其中APT攻击呈高发态势,是企业需要关注的安全问题。事实上,APT攻击发生的基本环境——网络,本身就是一个由计算机等元素构成的网络结构,这也不难联想到使用图数据结构来表达这些元素间的关系,再将攻击检测问题转化为图中的节点、边或子图分类任务。图嵌入是一个丰富且极具研究空间的问题,如何提高模型训练效率、创新模型构造方法、将图嵌入的思想应用于更多的生产实践,企业需要通过更进一步的研究,才能找到更好的答案。
参考文献
[1]Xu M. Understanding graph embedding methods and their applications[J]. SIAM Review, 2021, 63(4): 825-853.
[2]Cai H, Zheng V W, Chang K C C. A comprehensive survey of graph embedding: Problems, techniques, and applications[J]. IEEE Transactions on Knowledge and Data Engineering, 2018, 30(9): 1616-1637.
[3]Goyal P, Ferrara E. Graph embedding techniques, applications, and performance: A survey[J]. Knowledge-Based Systems, 2018, 151: 78-94.