机器学习能够处理海量数据,解决复杂场景下的科学难题,带领科学探索抵达过去无法触及的新领域。比如 DeepMind 用人工智能软件 AlphaFold 对科学界已知的几乎所有蛋白质结构进行了高度准确的预测;Christian Lagemann 提出的基于深度学习的粒子图像测速 (PIV) 方法一改原本的纯手动设置参数,大大提升模型的应用范围,对汽车、航空航天和生物医学工程等多个领域的研究具有至关重要的意义。
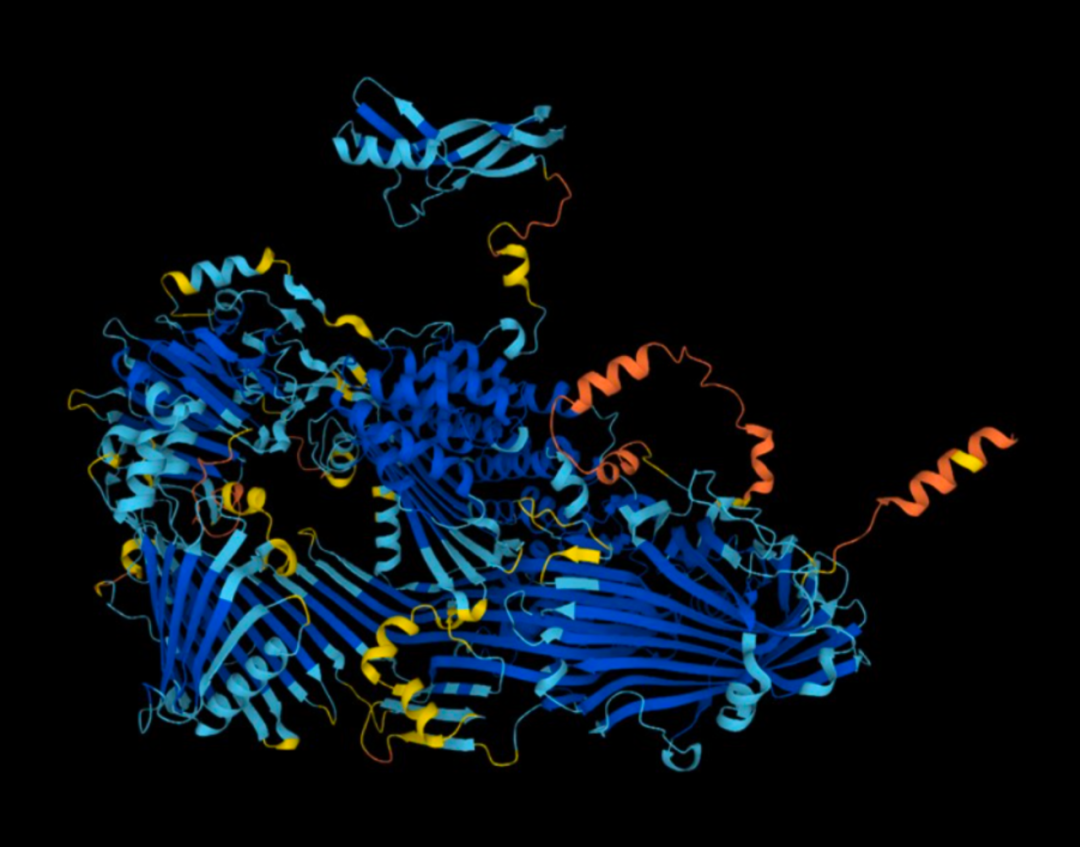
AlphaFold 能够预测出几乎所有已知蛋白质的结构(图源:DeepMind)
有充足的数据,有一个准确的模型来描述求解的科学问题,很多基础科学的 “百年未解之谜” 都能被机器学习迎刃而解。比如流体力学、凝聚态物理学、有机化学等等。
最近,字节跳动 AI Lab Research 团队和北京大学物理学院陈基课题组的工作《 Ab initio calculation of real solids via neural network ansatz》 给出了研究凝聚态物理的新思路,该工作提出了业内首个适用于固体系统的神经网络波函数,实现了固体的第一性原理计算,并将计算结果推向了热力学极限。其有力地证明了神经网络是研究固体物理的高效工具,也预示着深度学习技术将在凝聚态物理中发挥越来越重要的作用。相关研究成果于 2022 年 12 月 22 日发表于国际顶级刊物 Nature Communication 杂志上。

论文链接:https://www.nature.com/articles/s41467-022-35627-1
研究背景及研究方法
精确求解固体系统的薛定谔方程是凝聚态物理的圣杯之一。在过去数十年的凝聚态研究中,密度泛函理论被广泛采用并取得了巨大成功。
密度泛函理论:一种研究多电子体系电子结构的量子力学方法。
尽管如此,密度泛函理论仍存在着诸多不足:对于复杂的强关联系统,密度泛函理论无法给出精确描述;在泛函挑选上也缺乏系统性提高自身精度的方法。近年来,相比于密度泛函理论,更为精确和通用的波函数方法得到了越来越多的关注和研究。
针对这一现状,字节跳动 AI Lab Research 团队联合北京大学物理学院陈基课题组设计了适用于固体系统的周期性神经网络波函数,并与量子蒙特卡洛方法结合,实现了对于固体系统的第一性原理计算。在该工作中,深度学习技术被首次应用于连续空间的固体系统研究,并将计算推向了热力学极限。
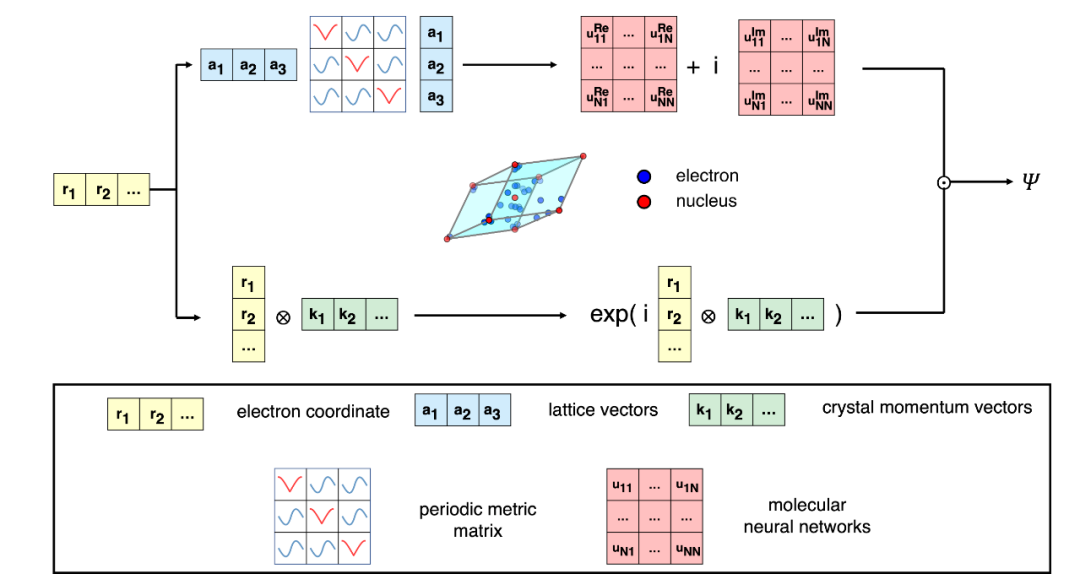
该工作的核心是将周期性推广后的系统特征向量与现有的分子神经网络波函数结合,构造出具有周期对称性和完全反对称性的固体系统波函数。之后,该工作运用量子蒙特卡洛方法高效地训练神经网络,并在一系列真实固体上进行了测试。
实验结果及分析
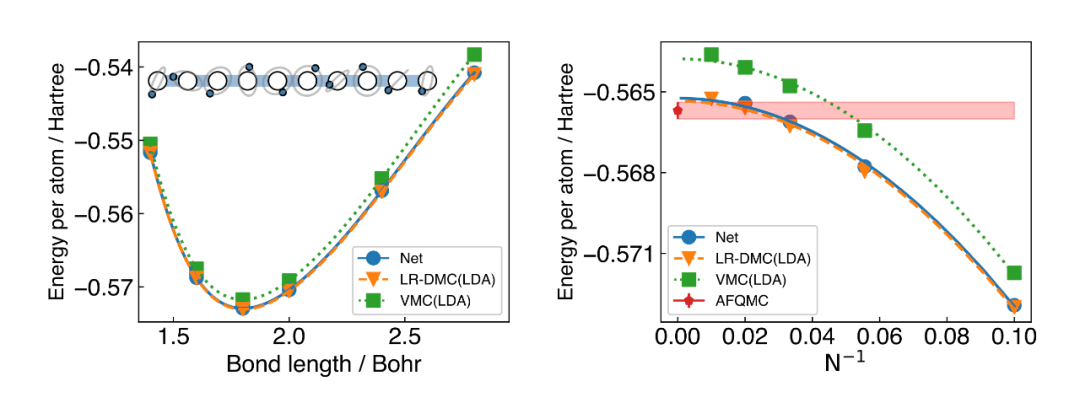
首先,作者在周期性的一维氢链上进行了测试。一维氢链是凝聚态中最为经典的系统之一,对于它的精确求解有助于人们理解强关联系统的特性。计算结果表明,神经网络可以达到与传统高精度方法(如辅助场蒙特卡洛)相近的精度。
随后,作者运用神经网络计算了二维石墨烯材料。石墨烯是近二十年来炙手可热的研究材料,它在导热、导电等方面的奇特性质具有重要的研究和应用价值。该工作精确计算了石墨烯的内聚能,计算结果与实验数据一致。
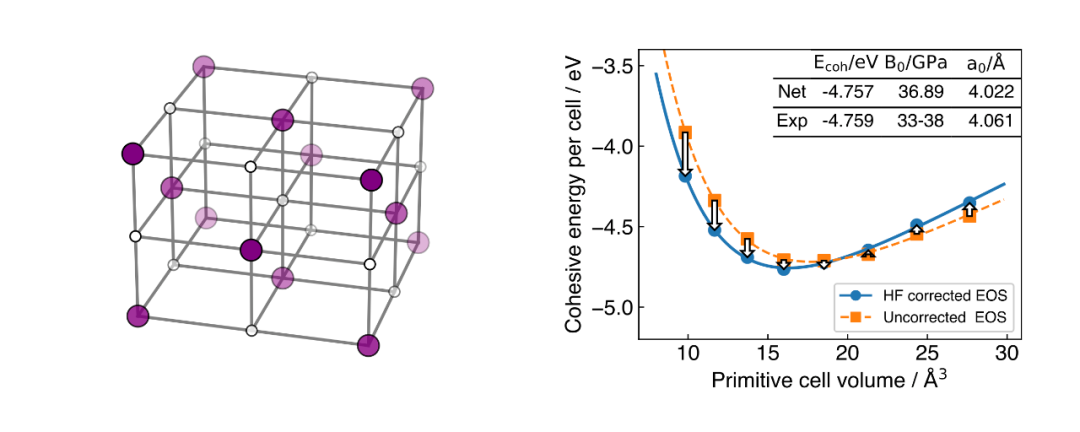
为了进一步验证工作的有效性,作者计算了三维的锂化氢材料并将计算规模推向了热力学极限,计算规模最大达到了 108 个电子,这也是至今为止神经网络所能模拟的最大固体系统。计算得到的材料内聚能,体积模量等均符合实验结果。
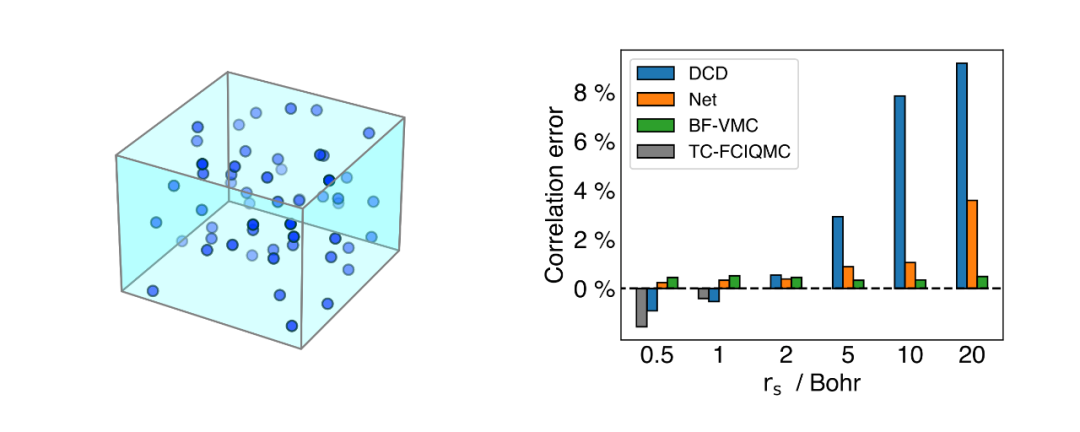
最后,作者研究了理论上更为有趣的均匀电子气系统。均匀电子气系统与许多新奇的物理效应(如量子霍尔效应)息息相关,因此深入理解均匀电子气具有重要的理论价值。计算结果表明,神经网络在均匀电子气上取得了不错的效果,接近甚至超越了许多传统高精度方法的结果。
该工作有力地证明了神经网络是研究固体物理的高效工具。随着算法的进一步完善,神经网络技术将在凝聚态物理中发挥更加重要的作用:如固体系统的相变,表面物理,非常规超导体等。这些课题的研究都需要高精度的固体波函数作为基石。同时,作者也在致力于研究更为高效的神经网络波函数,为凝聚态物理的研究提供更多可能性。