排序算法对于每个程序员来说,无疑是最常见的算法之一了。几乎每个新入行的程序员,在面试之前都会准备好一两种排序算法,例如冒泡排序、归并排序、快速排序之类的。而面试官们很多也都会现场让应聘者写一个简单的排序算法,来考验对方的基本功怎么样。
排序算法是让无序的数据变得有序起来,而反过来,让有一定顺序的数据变得无序起来,那么这个算法就是洗牌算法。洗牌算法是生活中常见的一种基础算法,最简单的应用就是在打扑克牌的时候,随机对扑克牌进行初始化。这时候要用到的算法就是洗牌算法。
大家在看王晶的赌王片里,肯定对于各种赌王的花式洗牌方法记忆很深刻。直观上来讲,洗牌算法非常好理解,无非就是把一副牌打乱。但是,什么样的结果才叫乱,很多人则说不太清楚了。
数学上,一个好的洗牌算法需要达到的目标是:在洗过牌之后,任意一张牌出现在任意位置的概率是一样的。例如对于n个数的洗牌算法,那么一张牌出现在任一位置的概率都是1/n,而洗牌算法最终的结果一共有n!种,即为数据的全排列。
这个目标很好理解,如果某种算法给出的结果是黑桃A在第一张的概率是50%,那么搞不好庄家就要吃大亏了。
所以洗牌算法最重要的就是结果要够乱。
最为经典的洗牌算法是Fisher-Yates Shuffle算法。该算法由Ronald A. Fisher 和 Frank Yates两人提出,其步骤如下:
1、初始化原始数组和新数组,数组长度设为n;
2、从还没有处理的数据中(假如还剩下k个),随机产生一个[0, k)之间的数字p;
3、从剩下的k个数中把第p个数字取出,按顺序放入新数组;
4、重复步骤2和3直到数字全部取完;
5、此时新数组中即是洗牌之后的数组。
下面我们证明一下该算法具有足够的随机性,即每个元素被放置在新数组中的第i个位置的概率是1/n。
证明:一个元素m被放入第i个位置的概率P = 前i-1个位置选择元素时没有选中m的概率 * 第i个位置选中m的概率,即
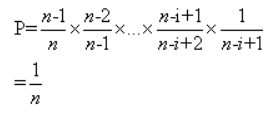
其中,第一次在n个中选没选到它,选中了另外n-1个的概率就是(n-1)/n,以此类推。
所以该算法具有足够的随机性。其时间复杂度为O(n*n),空间复杂度为O(n)。
后来Knuth和Durstenfeld在该算法基础上进行了改变,在原始数组上对数字进行交换,从而节省了额外的数组空间。该算法的基本思想和Fisher算法类似,只不过每次从未处理的数据中随机取出一个数字,然后把该数字放在数组的尾部,即把已经处理的数字存放在数组尾部。Knuth-Durstenfeld Shuffle算法是当前最为常用的洗牌算法。
































