这篇《Fast Counterfactual Inference for History-Based Reinforcement Learning》提出一种快速因果推理算法，使得因果推理的计算复杂度大幅降低——降低到可以和online 强化学习相结合的程度。
本文理论贡献主要有两点：
1、提出了时间平均因果效应的概念；
2、将著名的后门准则从单变量干预效应估计推广到多变量干预效应估计，称之为步进后门准则。
背景
需要准备关于部分可观测强化学习和因果推理的基础知识。这里不做过多介绍，给几个传送门吧：
部分可观测强化学习：
POMDP讲解 https://www.zhihu.com/zvideo/1326278888684187648
因果推理：
深度神经网络中的因果推理 https://zhuanlan.zhihu.com/p/425331915
动机
从历史信息中提取/编码特征是解决部分可观测强化学习的基本手段。主流方法是使用sequence-to-sequence（seq2seq）模型来编码历史，比如领域内流行使用的LSTM/GRU/NTM/Transformer的强化学习方法都属于这一类。这一类方法的共同之处在于，根据历史信息和学习信号（环境奖励）的相关性来编码历史，即一个历史信息的相关性越大所分配的权重也就越高。
然而，这些方法不能消除由采样导致的混杂相关性。举一个捡钥匙开门的例子，如下图所示：
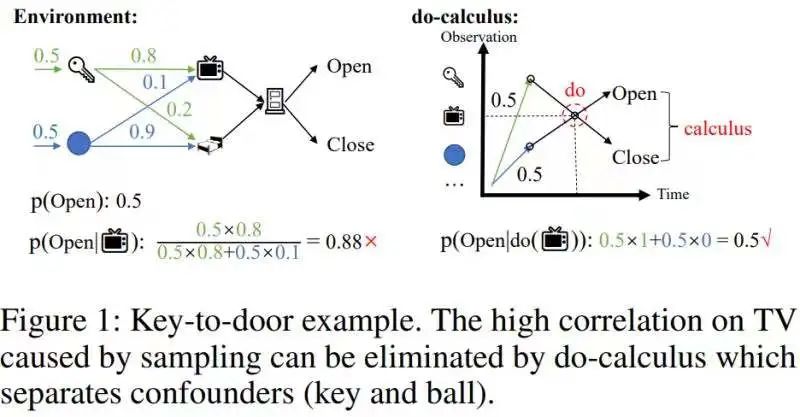
在这里agent能否开门只取决于历史上是否有拿到过钥匙，而不取决于历史上的其他状态。然而，如果agent的采样策略是对一些路径有偏好的，就会导致这些偏好路径上的状态具有高相关性。比如agent拿到钥匙之后，倾向于走 （上面那条路）开门而不是走 去开门（下面那条路）的话，就会使得开门这件事情和电视机有很高的相关性。这一类非因果但高度相关的状态就会被seq2seq赋予比较高的权重，使得编码的历史信息非常冗余。在这个例子里，当我们估计电视机和开门之间的相关性时，由于钥匙的存在，两者产生了混杂的高相关性。要估计电视机对开门的真实效应，就要去除这种混杂的相关性。
这种混杂相关性可以通过因果推理中的do-calculus来去除[1]：分离可能造成混淆的后门变量钥匙和球，从而切断后门变量（钥匙/球）和电视机之间的统计相关性，然后将p(Open| ，钥匙/球)的条件概率关于后门变量（钥匙/球）进行积分（Figure 1右图），得到真实的效应p(Open|do( ))=0.5。由于有因果效应的历史状态相对稀疏，当我们去除混杂的相关性以后，可以大幅压缩历史状态的规模。
因此，我们希望用因果推理来去除历史样本中混杂的相关性，然后再用seq2seq来编码历史，从而获得更紧凑的历史表征。（本文动机）
[1]注：这里考虑的是使用后门调整的do-calculus，附一个科普链接https://blog.csdn.net/qq_31063727/article/details/118672598
困难
在历史序列中执行因果推理，不同于一般的因果推理问题。历史序列中的变量既有时间维也有空间维，即观测-时间组合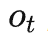
,其中o是观测，t是时间戳（相比之下MDP就很友好了，马尔可夫状态只有空间维）。两个维度的交叠，使得历史观测的规模相当庞大——用
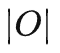表示每个时间戳上的观测取值个数，用T来表示时间总长度，则历史状态的取值有 
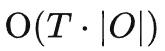种（其中正体O( )为复杂度符号）。[2]
以往的因果推理方法基于单变量干预检测，一次只能do一个变量。在具有庞大规模的历史状态上进行因果推理，将造成极高的时间复杂度，难以和online RL算法相结合。
[2]注：单变量干预因果效应的正式定义如下
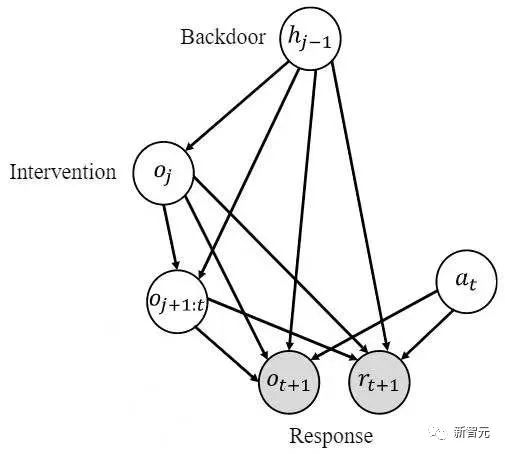
如上图所示，给定历史 ，要估计对转移变量 的因果效应，做以下两步：1）干预历史状态do ，2）以先前的历史状态 为后门变量，为响应变量，计算如下积分即为所要求取的因果效应
既然单变量干预检测难以和online RL相结合，那么开发多变量干预检测方法就是必须的了。
思路
本文的核心观察（假设）是，因果状态在空间维上稀疏。这个观察是自然而普遍的，比如拿钥匙开门，过程中会观测到很多状态，但钥匙这个观测值才决定了是否能开门，这个观测值在所有观测取值中占比稀疏。利用这个稀疏性我们可以通过多变量干预一次性就筛除掉大量没有因果效应的历史状态。但是时间维上因果效应并不稀疏，同样是拿钥匙开门，钥匙可以被agent在绝大部分时刻都观测到。时间维上因果效应的稠密性会妨碍我们进行多变量干预——无法一次性去除大量没有因果效应的历史状态。
基于上述两点观察，我们的核心思路是，先在空间维上做推理，再在时间维上做推理。利用空间维上的稀疏性大幅减少干预的次数。为了单独估计空间因果效应，我们提出先求取时间平均因果效应，就是把多个历史状态的因果效用在时间上进行平均（具体定义请见原文）。
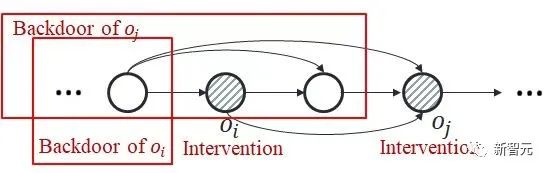
基于这个idea，我们将问题进行聚焦：要解决的核心问题是如何计算干预多个不同时间步上取值相同的变量(记作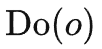
)的联合因果效应。这是因为后门准则不适用于多个历史变量的联合干预：如下图所示，考虑联合干预双变量
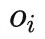和
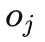，可以看到，时间步靠后的
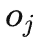的一部分后门变量里包含了
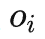，两者不存在公共的后门变量。
方法
我们改进后门准则，提出一个适用于估计多变量联合干预效应估计的准则。对于任意两个被干预的变量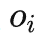
和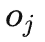
(i<j)，我们给出用于估计它们的联合干预效应的准则，如下
步进后门调整准则(step-backdoor adjustment formula)
该准则分离了，介于相邻两个时间步的变量之间的其他变量，称为步进后门变量。在满足这个准则的因果图中，我们可以估计任意两个被干预变量的联合因果效应。包括两步：step 1、以时间步上小于i的变量作为后门变量，估计do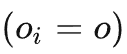
因果效应；step 2、以取定的
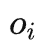后门变量和取定的
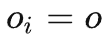为条件，以介于
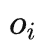和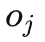
之间的变量为新的关于
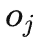的后门变量（即关于
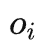和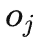
步进后门变量），估计do
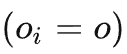的条件因果效应。则联合因果效应为这两部分的乘积积分。步进后门准则将普通的后门准则使用了两步，如下图所示
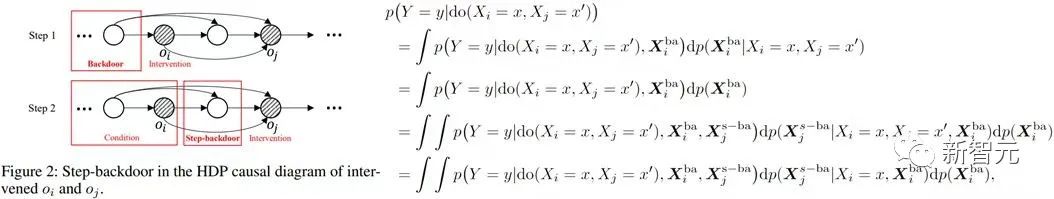
上式使用了更一般的变量表示符X。
对于三个变量以上的情况，通过连续使用步进后门准则——将每两个时间步相邻的干预变量之间的变量视作步进后门变量，连续计算上式，可以得到多变量干预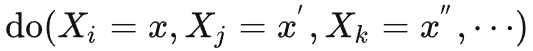
的联合因果效应如下：
Theorem 1. Given a set of intervened variables with different timestamps, if every two temporally adjacent variables meet the step-backdoor adjustment formula, then the overall causal effect can be estimated with
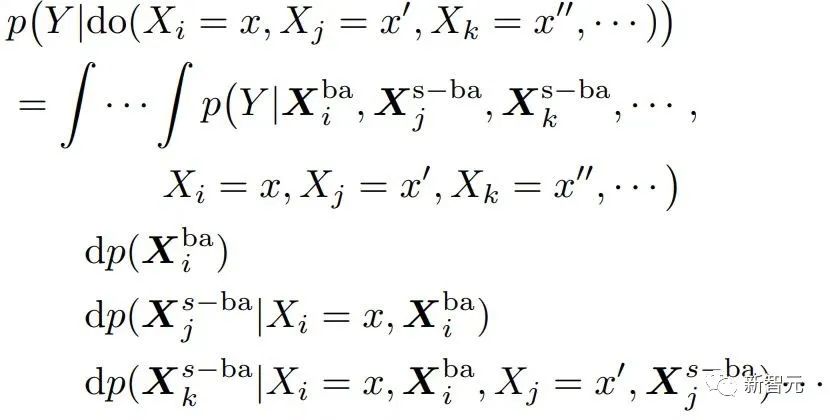
具体到部分可观测强化学习问题上，用观测o替换上式的x后，有如下因果效应计算公式：
Theorem 2. Given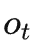 
and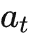 
, the causal effect of Do(o) can be estimated by
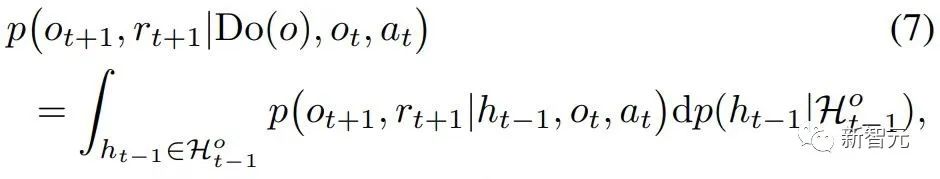
至此，论文给出了计算空间因果效应（即时间平均因果效应）的公式，这一段方法将干预的次数由O(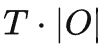
）降低为O（
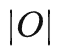）。接下来，就是利用（本章开头提及）空间因果效应的稀疏性，进一步对干预次数完成指数级缩减。将对一个观测的干预替换为对一个观测子空间的干预——这是一个利用稀疏性加速计算的通常思路（请见原文）。在本文中，开发了一个称为Tree-based history counterfactual inference （T-HCI）的快速反事实推理算法，这里不作赘述（详见原文）。其实基于步进后门准则后续还可以开发很多历史因果推理算法，T-HCI只是其中的一个。最后的结果是Proposition 3 (Coarse-to-fine CI). If
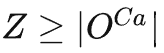, the number of interventions for coarse-to-fine CI is
）。
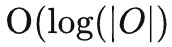算法结构图如下
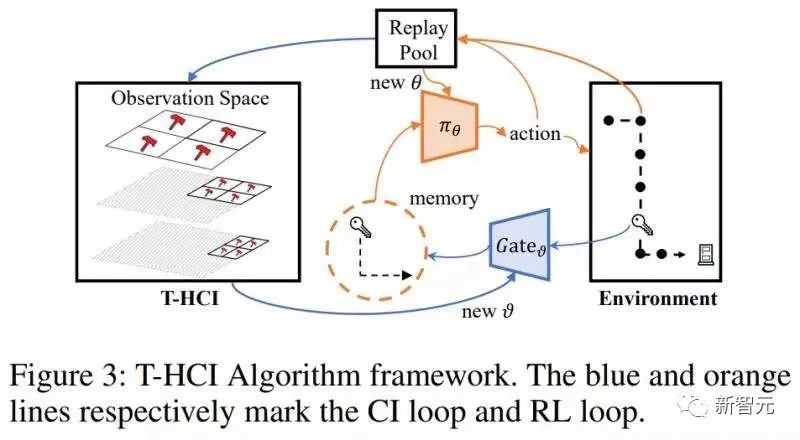
算法包含两个loops，一个是T-HCI loop，一个是策略学习loop，两者交换进行：在策略学习loop里，agent被采样学习一定回合数量，并将样本存在replay pool中；在T-HCI loop中，利用存储的样本进行上述的因果推理过程。
Limitations：空间维上的因果推理对历史规模的压缩幅度已经足够大了。尽管时间维上做因果推理可以进一步压缩历史规模，但考虑到计算复杂度需要平衡，本文在时间维上保留了相关性推理（在有空间因果效应的历史状态上端到端使用LSTM），没有使用因果推理。
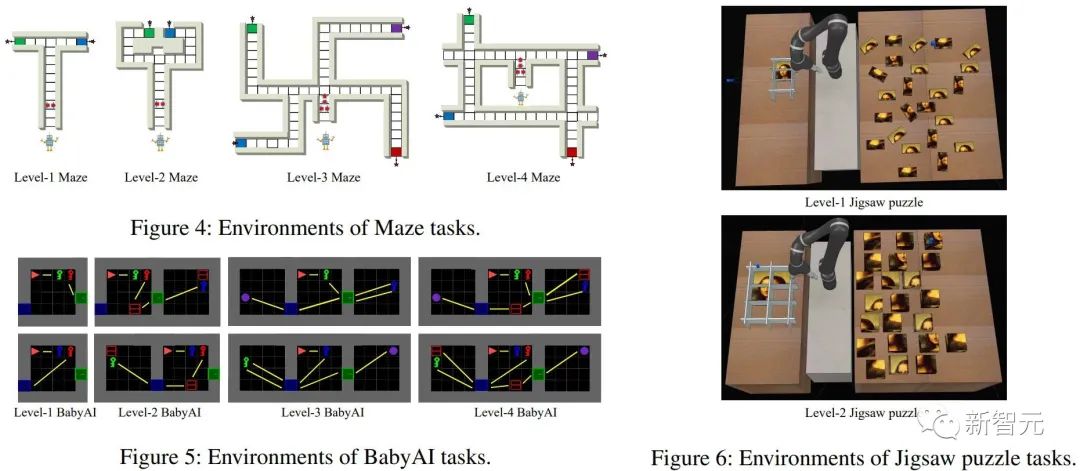
验证
实验上验证了三个点，回应了前面的claims：1) Can T-HCI improve the sample efficiency of RL methods? 2) Is the computational overhead of T-HCI acceptable in practice? 3) Can T-HCI mine observations with causal effects? 详见论文的实验章节，这里就不占用篇幅了。当然，有兴趣的小伙伴还可私信我/评论哦。
未来可拓展的方向
说两点，以抛砖引玉：
1、HCI不限于强化学习的类型。虽然本文研究的是online RL，但HCI也可自然地拓展到offline RL、model-based RL等等，甚至于可以考虑将HCI应用于模仿学习上；
2、HCI可以视作一种特殊的hard attention方法——有因果效性的序列点获注意力权值1，反之获注意力权值0。从这个角度看，一些序列预测问题也可能尝试使用HCI来处理。
