Openharmony 军棋工兵寻径算法的实现-军棋工兵对工兵

一、引言

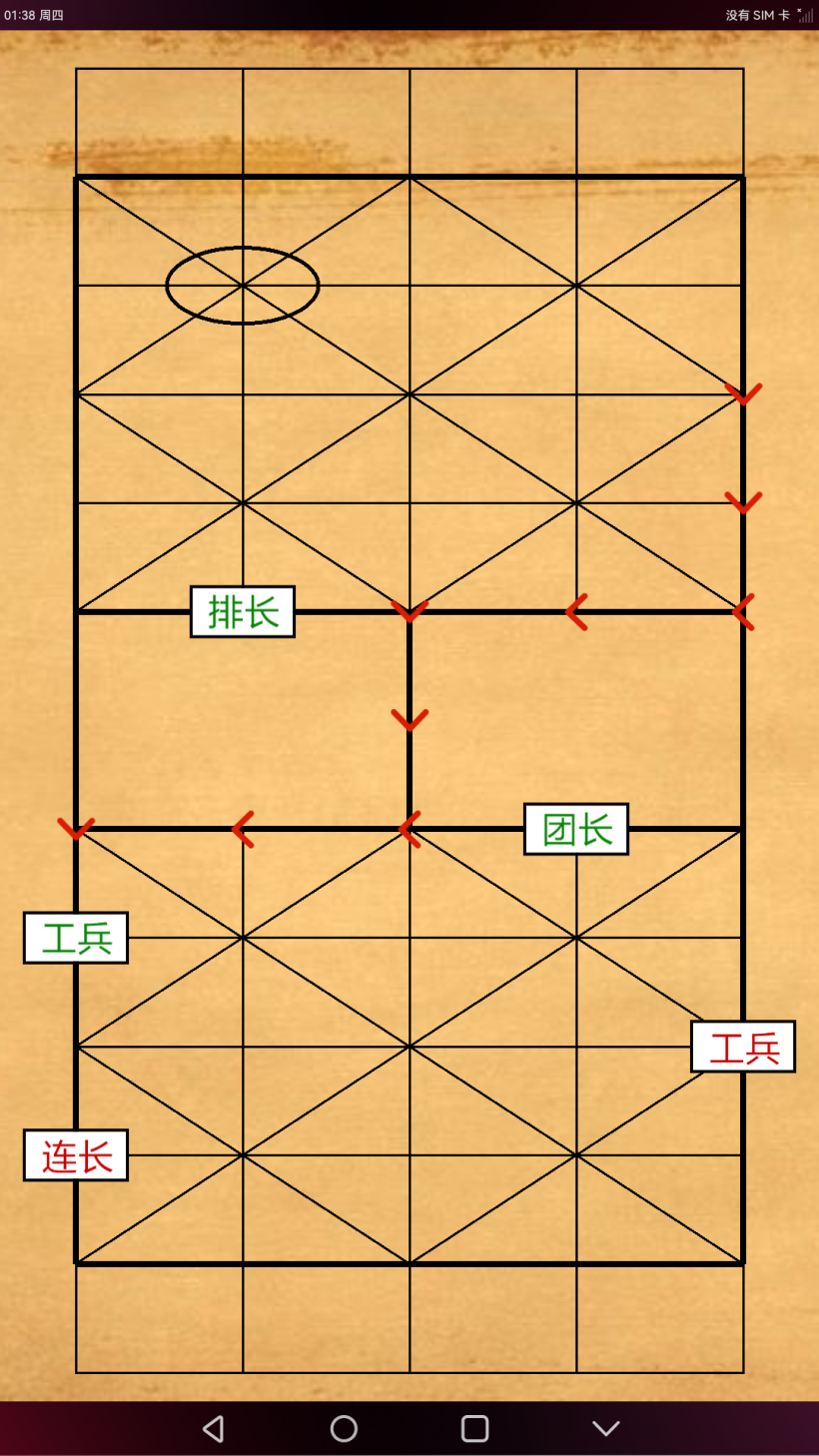
工兵可在铁路线上任意行走,其它棋子在铁路线上只能直走或经过弧形线,不能转直角弯; 工兵在普通路线上跟其他棋子一样,走一格。但是在轨道上,就如入无人之地了。可以在轨道上自由移动,怎样走都行,只要不超过轨道的区域,想走多远就走多远,但是如果有个棋子(不论敌我)堵住路线,你就不能按照那个路线行进；同时我们还要寻找到最近的路径。

openharmony 军棋工兵寻径算法的实现-开源基础软件社区

二、算法分析

大体要求

1、工兵从起点到终点过程中不能有障碍物阻挡。

2、如何寻求到路径最短？且是否用时最快。

3、也有可能起点到终点是死路。

军旗的工兵走法特别像迷宫走法。

迷宫算法

1、深度优先搜索（DFS）

它和递归的探测思路是基本一致的，可以看成是递归方式的非递归版本。

2、广度优先搜索（BFS）

广度优先搜索法利用队列的特点，一层层向外扩展查找可走的方块，直到找到出口为止，最先找到的这个答案就必然是最短的。

3、根据特点我们希望最先找到最短的距离故采用bfs的方式。

采用队列来记录探测点；当前探测点的四个方向，可以通过的点，保存到这个队列中，并移除当前探测点。

openharmony 军棋工兵寻径算法的实现-开源基础软件社区

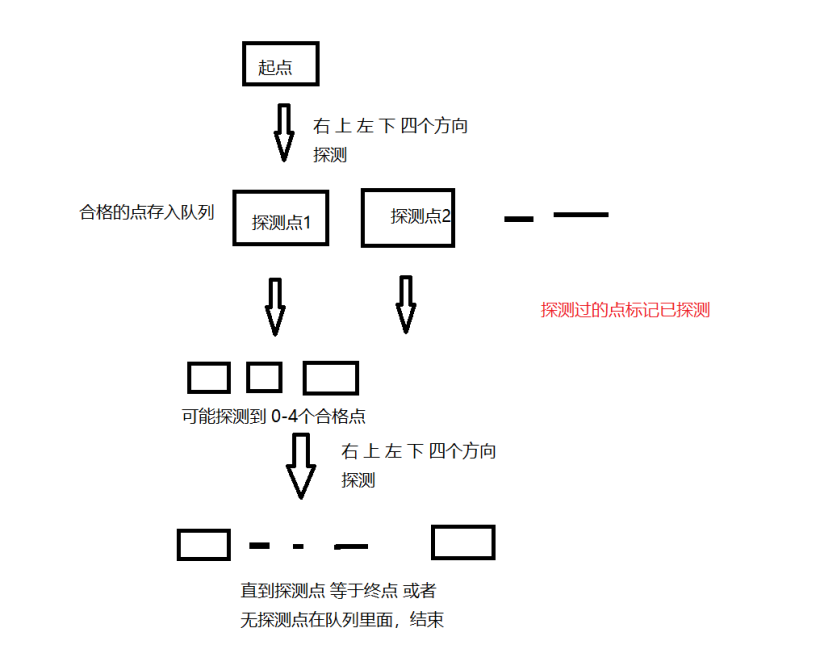
右下左上的四个方向探测。

openharmony 军棋工兵寻径算法的实现-开源基础软件社区

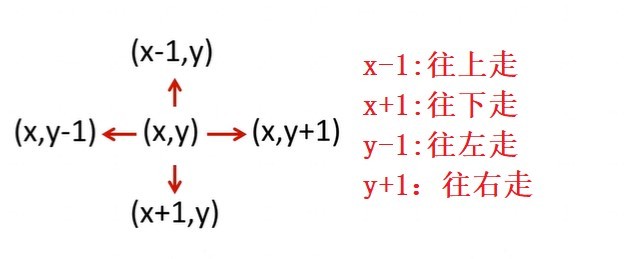
采用一个二维数组来存储 x,y上的障碍物，和探测的点。

let noChessBoard: number[][] = [ // a[j][h]代表j行h列数据  // 1,行：row 2、列：column  export const ROW = 12  export const COLUMN = 4
    [1, 1, 1, 1, 1],
    [0, 0, 0, 0, 0],
    [0, 1, 1, 1, 0],
    [0, 1, 1, 1, 0],
    [0, 1, 1, 1, 0],
    [0, 0, 0, 0, 0],
    [0, 1, 0, 1, 0],
    [0, 0, 0, 0, 0],
    [0, 1, 1, 1, 0],
    [0, 1, 1, 1, 0],
    [0, 1, 1, 1, 0],
    [0, 0, 0, 0, 0],
    [1, 1, 1, 1, 1]]

代码实现

（1）获取到起点和终点坐标。

this.routeNode = this.engineerRoute(firstChess, moveChess);

（2）获取二维数组迷宫标记。

二维数组是记录棋盘上 0 是表示可通状态，1表示不可通。默认是棋盘铁路都为0可通。

然后，敌方和友方其中全部设置为不可通1。

// 工兵路径寻找 （bfs 广度优先搜索）
private engineerRoute(start: Chess, end: Chess): RouteNode {
    let noChessBoard: number[][] = [ // a[j][h]代表j行h列数据  // 1,行：row 2、列：column  export const ROW = 12  export const COLUMN = 4
        [1, 1, 1, 1, 1],
        [0, 0, 0, 0, 0],
        [0, 1, 1, 1, 0],
        [0, 1, 1, 1, 0],
        [0, 1, 1, 1, 0],
        [0, 0, 0, 0, 0],
        [0, 1, 0, 1, 0],
        [0, 0, 0, 0, 0],
        [0, 1, 1, 1, 0],
        [0, 1, 1, 1, 0],
        [0, 1, 1, 1, 0],
        [0, 0, 0, 0, 0],
        [1, 1, 1, 1, 1]]

    for (let i = 0;i < this.aList.length; i++) {
        let a = this.aList[i]
        noChessBoard[a.y][a.x] = 1
    }
    for (let i = 0;i < this.bList.length; i++) {
        let b = this.bList[i]
        noChessBoard[b.y][b.x] = 1
    }

    return this.bfs(start, end, noChessBoard)
}

（3）进行广度优先搜索。

private bfs(start: Chess, end: Chess, roads: number[][]): RouteNode{
    Logger.d(TAG, `bfs roads:${JSON.stringify(roads)}`)
    Logger.d(TAG, `bfs start:${JSON.stringify(start)}`)
    Logger.d(TAG, `bfs end:${JSON.stringify(end)}`)
    let routeQueue = new MyArrayQueue()
    let first = new RouteNode(start.x, start.y, 0)
    routeQueue.push(first)
    while (routeQueue.size() != 0) {
        Logger.d(TAG, `bfs scan while routeQueue:${JSON.stringify(routeQueue)}`)
        let node = routeQueue.pop()
        Logger.d(TAG, `bfs scan pop node:${JSON.stringify(node)}`)
        let x = node.x
        let y = node.y
        if (x === end.x && y === end.y) {
            return node
            // break
        }
        for (var i = 0; i < 4; i++) {
            let tx = x + this.dx[i]
            let ty = y + this.dy[i]
            Logger.d(TAG, `bfs scan tx:${tx} ty:${ty}`)
            if (tx >= 0 && tx <= COLUMN && ty >= 0 && ty <= ROW && roads[ty][tx] === 0) { // 如果该位置可以走动
                // 入队
                Logger.d(TAG, `bfs add tx:${tx} ty:${ty}`)
                let temp = new RouteNode(tx, ty, node.step + 1)
                temp.prev = node
                routeQueue.push(temp)
                Logger.d(TAG, `bfs scan push :${JSON.stringify(routeQueue)}`)
                roads[ty][tx] = 1
            }
        }
        // 扩展完
        Logger.d(TAG, `bfs scan one end...`)
    }
    return null
}

（4）本案例还记录路径，采用的是链表数据结构。

每次把prev给记录下来。这下就可以追溯到整个完整的探测路线。

export class RouteNode extends Point {
    prev: RouteNode ; //前一个节点
    next: RouteNode  ; //下一个节点
    step: number
    constructor(x: number, y: number, step: number) {
        super(x, y)
        this.step = step
    }
}

（5）队列是自己利用数组改成的。

openharmony 目前 Deque、Queue 有bug，没法用；只能用数组，然后数组的pop是最后一个，就把探测顺序插入第一个。

export class MyArrayQueue {
    nodes: RouteNode[]
    constructor() {
        this.nodes = new Array
    }

    push(node: RouteNode) {
        Logger.d(TAG, `push ...:${JSON.stringify(node)}`)
        this.nodes.unshift(node)
        Logger.d(TAG, `push end.:${JSON.stringify(this.nodes.length)}`)
    }

    pop(): RouteNode{
        return this.nodes.pop()
    }

    size() {
        return this.nodes.length
    }
}

三，总结

可能代码直接拷贝过去跑不通。

本文也就阐述一种思维，同时体现一下openharmony目的能力可达之处。

想了解更多关于开源的内容，请访问：

51CTO 开源基础软件社区

https://ost.51cto.com