1996年的8月19日至23日，芬兰的瓦萨举行了由芬兰人工智能协会和瓦萨大学组织的芬兰人工智能会议。
会议上发表的一篇论文证明：图灵机就是一个循环神经网络。
没错，这是在26年前！
让我们来看一看，这篇发表于1996年的论文。
1 前言
1.1 神经网络分类
神经网络可用于分类任务，判断输入模式是否属于特定的类别。
长期以来，人们都知道单层前馈网络只能用于对线性可分的模式进行分类，即连续层越多，类的分布就越复杂。
当在网络结构中引入反馈时，感知器输出值被循环利用，连续层的数量原则上变为无限大。
算力有没有质的提升？答案是肯定的。
例如，可以构造一个分类器来判断输入整数是否为素数。
事实证明，用于此目的的网络大小可以是有限的，即使输入整数大小不受限制，可以正确分类的素数数量也是无限的。
在本文中，「由相同计算元素组成的循环网络结构」可用于完成任何（算法上的）可计算功能。
1.2 关于可计算性
根据可计算性理论的基本公理，可以使用图灵机实现可计算函数，有多种方法可以实现图灵机。
定义程序语言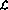
。该语言有四种基本操作：
这里，V代表任何具有正整数值的变量，j代表任何行号。
可以证明，如果一个函数是图灵可计算的，则可以使用这种简单的语言对其进行编码（有关详细信息，请参见[1]）。
2 图灵网络
2.1 递归神经网络结构
本文研究的神经网络由感知器组成，它们都具有相同的结构，感知器数q的运算可以定义为
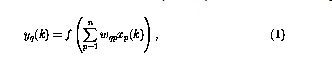
其中，当前时刻的感知器输出（用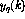
表示）是使用n输入
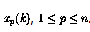计算的。
非线性函数f现在可定义为
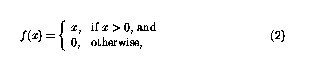
这样函数就可以简单地「切断」负值，感知器网络中的循环意味着感知器可以以复杂的方式组合。
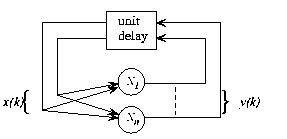
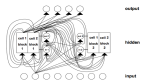
图1 递归神经网络的整体框架，结构自主无外部输入，网络行为完全由初始状态决定
在图1中，递归结构显示在一个通用框架中：现在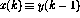
和n是感知器的数量，从感知器p到感知器q的连接由（1）中的
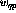标量权重表示。
即给定初始状态，网络状态会迭代到不再发生变化，结果可以在该稳定状态或网络的「固定点」下读取。
2.2 神经网络建构
接下来阐述该程序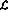
如何在感知器网络中实现。该网络由以下节点（或感知器）组成：
- 对于程序中的每个变量V，都有一个变量节点
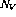。 - 对于每个程序行i，都有一个指令节点
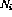。 - 对于第i行上的每个条件分支指令，另外还有两个转移节点
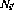和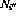
。
语言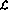
程序的实现包括感知器网络的以下变化：
- 对于程序中的每个变V，使用以下链接扩充网络：
- 如果程序代码的第i行没有操作(
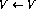)，则使用以下链接扩充网络（假设该节点
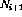存在：
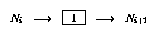
- 如果第i行有增量操作(
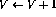)，则按如下方式扩充网络：
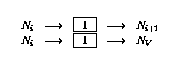
- 如果第i行有递减操作(
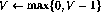)，则按如下方式扩充网络：
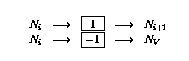
- 如果第i行有条件分支(
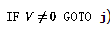)，则按如下方式扩充网络：
2.3 等效性证明
现在需要证明的是，「网络的内部状态或网络节点的内容」，可以用程序状态来标识，同时网络状态的连续性与程序流对应。
定义网络的「合法状态」如下：
- 至所有转换节点
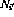和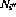
（如2.2中所定义）的输出为零(
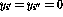)； - 至多一个指令节点
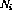有单位输出(
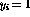)，所有其他指令节点有零输出，并且 - 变量节点具有非负整数输出值。
如果所有指令节点的输出均为零，则状态最终状态。一个合法的网络状态可以直接解释为一个程序「快照」——如果，程序计数器在第i行，相应的变量值存储在变量节点中。
网络状态的变化是由非零节点激活的。
首先，关注变量节点，事实证明它们表现为积分器，节点的先前内容被循环回同一节点。
从变量节点到其他节点的唯一连接具有负权重——这就是为什么包含零的节点不会改变，因为非线性的原因（2）。
接下来，详细说明指令节点。假设唯一的非零指令节点在时间k---这对应于程序计数器在程序代码中第i行。
若程序中第i行是，则网络向前一步的行为可表示为（只显示受影响的节点）
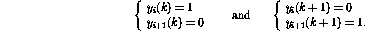
事实证明，新的网络状态再次合法。与程序代码相比，这对应于程序计数器被转移到第i+1行。
另一方面，如果程序中的第i行是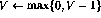
，则向前一步的行为是
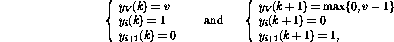
这样，除了将程序计数器转移到下一行之外，变量V的值也会递减。如果第i行是
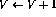，网络的操作将是相同的，除了变量V的值增加。
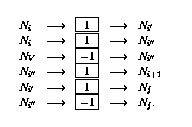
第i行的条件分支操作（IF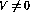 
GOTO j）激活更复杂的操作序列：
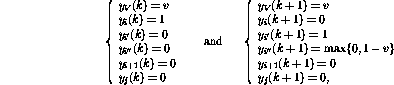
最后，
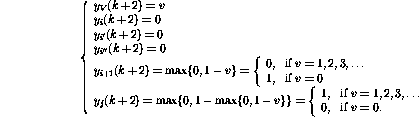
事实证明，在这些步骤之后，网络状态可以再次被解释为另一个程序快照。
变量值已更改，token已转移到新位置，就像执行了相应的程序行一样。
如果token消失，网络状态不再改变——这只有在程序计数器「超出」程序代码时才会发生，这意味着程序终止。
网络的运行也类似对应程序的运行，证明完成。
3 修改
3.1 扩展
定义额外的流线型指令很容易，这些指令可以使编程更容易，并且生成的程序更具可读性和执行速度。例如，
- 第i行的无条件分支（GOTO j）可以实现为
- 将常量c添加到第i行的变量（）可以实现为
- 行i上的另一种条件分支（IF V=0 GOTO j ）可以实现为
- 此外，可以同时评估各种递增/递减指令。假设要执行以下操作：。只需要一个节点：
上述方式绝不是实现图灵机的唯一途径。
这是一个简单的实现，在应用程序中不一定是最佳的。
3.2 矩阵制定
上述构造也可以以矩阵的形式实现。
基本思想是将变量值和「程序计数器」存储在进程状态s中，并让状态转换矩阵A代表节点之间的链接。
矩阵结构的运算可以定义为一个离散时间的动态过程
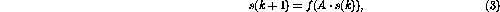
其中非线性向量值函数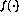
现在按元素定义，如（2）中所示。
状态转移矩阵A的内容很容易从网络公式中解码出来——矩阵元素是节点之间的权重。
该矩阵公式类似于[3]中提出的「概念矩阵」框架。
4 例子
假设要实现一个简单的函数y=x，也就是说，输入变量x的值应该传递给输出变量y。使用语言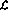
可以将其编码为（让「入口点」现在不是第一行而是第三行）：
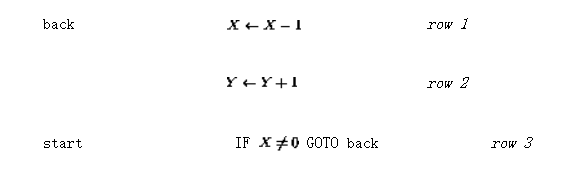
生成的感知器网络如图2所示。
实线代表正连接（权重为1），虚线代表负连接（权重-1）。与图1相比，重新绘制了网络结构，并通过在节点中集成延迟元件来简化网络结构。
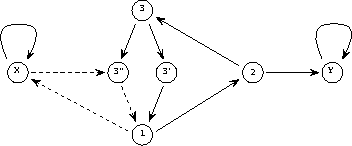
图2 简单程序的网络实现
在矩阵形式中，上面的程序看起来像
矩阵A中的前两行/列对应于连接到代表两个变量Y和X的节点的链接，接下来的三行代表三个程序行（1、2和3），最后两个代表分支指令所需的附加节点（3'和3''）。
然后是初始（迭代前）和最终（迭代后，找到固定点时）的状态
如果变量节点的值将严格保在0和1之间，则动态系统（3）的操作将是线性的，该函数根本没有影响。
原则上，然后可以在分析中使用线性系统理论。
例如，在图3中，示出了状态转移矩阵A的特征值。
即使在上面的例子中单位圆外有特征值，非线性使得迭代总是稳定的。
事实证明，迭代总是在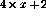
步骤之后收敛，其中
。
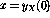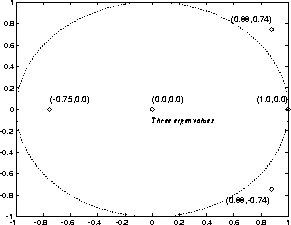
图3 简单程序的「特征值」
5 讨论
5.1 理论方面
结果表明，图灵机可以编码为感知器网络。
根据定义，所有可计算函数都是图灵可计算的——在可计算性理论的框架内，不存在更强大的计算系统。
这就是为什么，可以得出结论——
循环感知器网络（如上所示）是图灵机的（又一种）形式。
这种等价的好处是可计算性理论的结果很容易获得——例如，给定一个网络和一个初始状态，就不可能判断这个过程最终是否会停止。
上述理论等价性并没有说明计算效率的任何信息。
与传统的图灵机实现（实际上是今天的计算机）相比，网络中发生的不同机制可以使一些功能在这个框架中更好地实现。
至少在某些情况下，例如，一个算法的网络实现可以通过允许snapshot向量中的多个「程序计数器」来被并行化。
网络的运行是严格本地的，而不是全局的。
一个有趣的问题出现了，例如，是否可以在网络环境中更有效地攻击NP完全问题！
与语言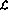
相比，网络实现具有以下「扩展」：
- 变量可以是连续的，而不仅仅是整数值。实际上，呈现实数的（理论）能力使网络实现比语言
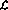更强大，所有以语言呈现的数字都是有理数。 - 可以同时存在各种「程序计数器」，并且控制的转移可能是「模糊的」，这意味着指令节点提供的程序计数器值可能是非整数。
- 一个较小的扩展是可自由定义的程序入口点。这可能有助于简化程序——例如，变量的复制在上面的三个程序行中完成，而名义解决方案（参见[1]）需要七行和一个额外的局部变量。
与原始程序代码相比，矩阵公式显然是比程序代码更「连续」的信息表示形式——可以（经常）修改参数，而迭代结果不会突然改变。
这种「冗余」也许可以在某些应用中使用。
例如，当使用遗传算法（GA）进行结构优化时，可以使遗传算法中使用的随机搜索策略更加高效：在系统结构发生变化后，可以搜索连续成本函数的局部最小值使用一些传统技术（参见[4]）。
通过示例学习有限状态机结构，如[5]中所述，可以知道：在这种更复杂的情况下也采用迭代增强网络结构的方法。
不仅神经网络理论可能受益于上述结果——仅看动态系统公式（3），很明显，在可计算性理论领域发现的所有现象也都以简单的形式存在——寻找非线性动态过程。
例如，停机问题的不可判定性是系统论领域的一个有趣贡献：对于任何表示为图灵机的决策过程，都存在形式（3）的动态系统，它违背了这个过程——对于例如，无法构建通用的稳定性分析算法。
5.2 相关工作
所呈现的网络结构与递归来Hopfield神经网络范式之间存在一些相似之处（例如，参见[2]）。
在这两种情况下，「输入」都被编码为网络中的初始状态，「输出」在迭代后从网络的最终状态中读取。
Hopfield网络的固定点是预编程的模式模型，输入是「噪声」模式——该网络可用于增强损坏的模式。
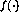中非线性函数的展望（2）使得上述「图灵网络」中可能的状态数量是无限的。
与单元输出始终为-1或1的Hopfield网络相比，可以看出，理论上，这些网络结构有很大不同。
例如，虽然Hopfield网络中的稳定点集是有限的，但以图灵网络为代表的程序通常具有无限数量的可能结果。
Hopfield网络的计算能力在[6]中进行了讨论。
Petri网是基于事件和并发系统建模的强大工具[7]。
Petri网由位和转移以及连接它们的弧组成。每个地方可能包含任意数量的token，token的分布称为Petri网的标记。
如果转换的所有输入位置都被标记占用，则转换可能会触发，从每个输入位置删除一个标记，并向其每个输出位置添加一个标记。
可以证明，具有附加抑制弧的扩展Petri网也具有图灵机的能力（参见[7]）。
上述图灵网与Petri网的主要区别在于Petri网的框架更为复杂，具有专门定制的结构，不能用简单的一般形式（3）来表达。
参考
1 Davis, M. and Weyuker, E.: Computability, Complexity, and Languages---Fundamentals of Theoretical Computer Science. Academic Press, New York, 1983.
2 Haykin, S.: Neural Networks. A Comprehensive Foundation. Macmillan College Publishing, New York, 1994.
3 Hyötyniemi, H.: Correlations---Building Blocks of Intelligence? In Älyn ulottuvuudet ja oppihistoria (History and dimensions of intelligence), Finnish Artificial Intelligence Society, 1995, pp. 199--226.
4 Hyötyniemi, H. and Koivo, H.: Genes, Codes, and Dynamic Systems. In Proceedings of the Second Nordic Workshop on Genetic Algorithms (NWGA'96), Vaasa, Finland, August 19--23, 1996.
5 Manolios, P. and Fanelli, R.: First-Order Recurrent Neural Networks and Deterministic Finite State Automata. Neural Computation 6, 1994, pp. 1155--1173.
6 Orponen, P.: The Computational Power of Discrete Hopfield Nets with Hidden Units. Neural Computation 8, 1996, pp. 403--415.
7 Peterson, J.L.: Petri Net Theory and the Modeling of Systems. Prentice--Hall, Englewood Cliffs, New Jersey, 1981.
参考资料：
